Unity 柏林噪声

工程源码GitHub地址：Unity-PerlinNoise

关于柏林噪声：

先粘贴关于百度百科的一段话：

柏林噪声 (Perlin noise )指由Ken Perlin发明的自然噪声生成算法。一个噪声函数基本上是一个种子随机发生器。它需要一个整数作为参数，然后根据这个参数返回一个随机数。如果两次都传同一个参数进来，它就会产生两次相同的数。这条规律非常重要，否则柏林函数只是生成一堆垃圾

但是百度百科中没有更多关于柏林噪声具体实现的步骤过程，而在维基百科有介绍到柏林噪声生成的大概的步骤：
在这里插入图片描述

整个过程简要的分为三部分：

选取随机点，给定随机值
给定点位的梯度（用插值函数标识）
根据随机点的值与梯度计算出为赋值位置的数值

在这一过程中Perlin Noise使用一些特殊的处理策略保证生成的数据伪随机并且连续

简单演绎一维柏林噪声：

根据维基百科的步骤叙述，来演绎一下一维柏林噪声的创建过程：

首先创建一个坐标系，以X轴作为一维坐标参考点位，Y轴作为以为坐标的参考值，这样就创建了一个基本的坐标系

先在一个一维数组上选择一些位置，为他们随机的赋值，而在这些点位中间的位置，就需要通过一些插值算法来获取到值，最终获取到一条连续的曲线

在上面的过程中，有几个关键的点：

如何选择赋值的位置
如何对其进行赋值
采用哪种插值方式获取非整数点的数值

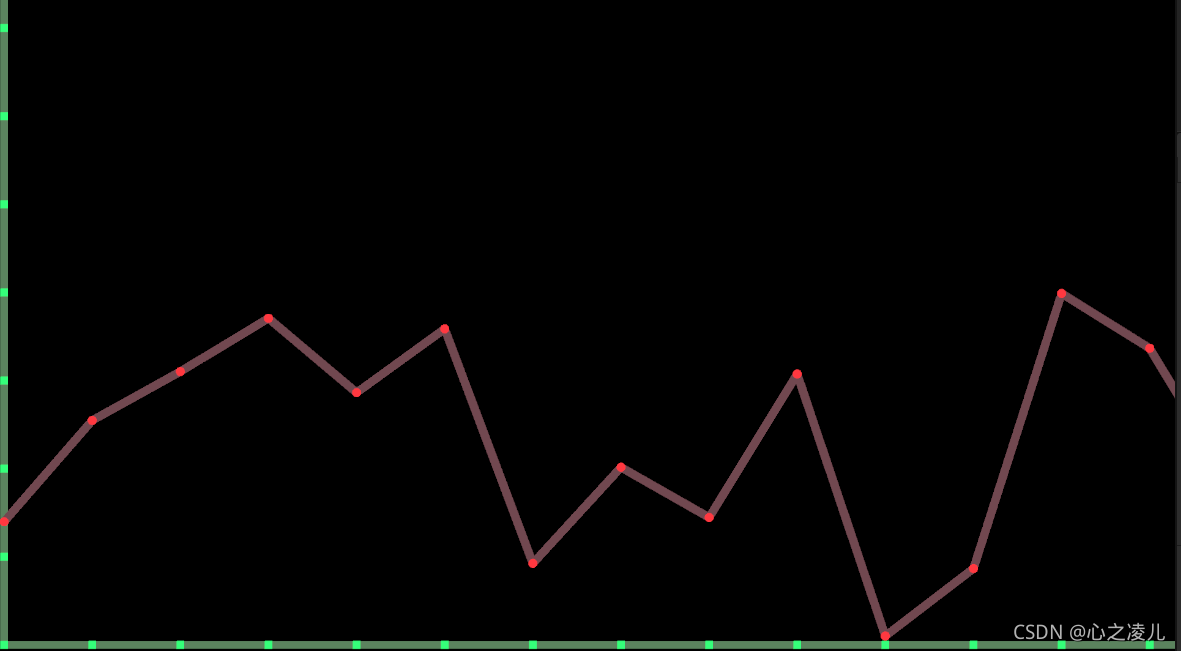
在一维的噪声生成案例中，我们可以根据X坐标轴来间隔取整获取这些点位，然后通过随机方法来为这些整数点赋值。接下来就可以在非整数点通过相邻的两个整数的数值插值计算出其对应的值，这样就可以得到一条连续的曲线，也就是一维的柏林噪声图，简单的写一个代码画出一个坐标轴，并基于Line Renderer绘制一维柏林噪声：

using System.Collections;
using System.Collections.Generic;
using UnityEngine;

public class PerlinNoise : MonoBehaviour
{
   
    public int lineWight;

    //public List<Vector3> points;
    public GameObject posPre;
    public Dictionary<int, Vector3> points = new Dictionary<int, Vector3>();
    public LineRenderer line;

    public int interIndexMax = 100;

    private void Awake()
    {
   
        CreatePos();
        CreateLine();
    }
    //画出整数点对应数值点位
    void CreatePos()
    {
   
        for (int i = 0; i < lineWight; i++)
        {
   
            float num = Random.Range(0f, 4f);

            Vector3 pointPos = new Vector3(i, num, 0);
            GameObject go = Instantiate(posPre, this.transform);
            go.transform.position = pointPos;
            points.Add(i, pointPos);
        }
    }
    //相邻两个整数点位之间插值获取其他位置数值
    void CreateLine()
    {
   
        int posIndex = 0;
        int interIndex;
        line.positionCount= interIndexMax * (points.Count - 1);
       	for (int i = 1; i < points.Count; i++)
        {
   
            interIndex = 0;
            while (interIndex< interIndexMax)
            {
   
                interIndex++;
                float posY = points[i - 1].y + (points[i].y - points[i - 1].y) * (interIndex / (float)interIndexMax);
                Vector3 pos = new Vector3(i - 1 + interIndex / (float)interIndexMax, posY, 0);
                line.SetPosition(posIndex, pos);
                posIndex++;
            }
        }
    }

在上面的代码中，可以看出，相邻的两个整数点之间会进行一次线性插值，来求出两点之间的具体曲线，运行代码后可以看到下面的效果：

在这里插入图片描述

在上面的一维柏林噪声生成中，我们基于线性插值获取到了一条连续的折线，由于程序会在相邻两个整数点之间进行一次线性插值获取到中间点的坐标。结果得到一条直线，同时在一个整数点的左右两边使用了不同的插值区间，结果使得两边的曲线在整数点的斜率不同，最终造成了Perlin Noise生成的一维曲线在整数点的不连续

为了避免上面的情况，使得得到的Perlin Noise更加平滑自然，Ken Perlin建议使用： $3t^{2}-2t^{3}$ 作为Perline Noise的插值函数，而在最新版本算法该插值函数又被更换为 $6t^{5}-15t^{4}+10t^{3}$

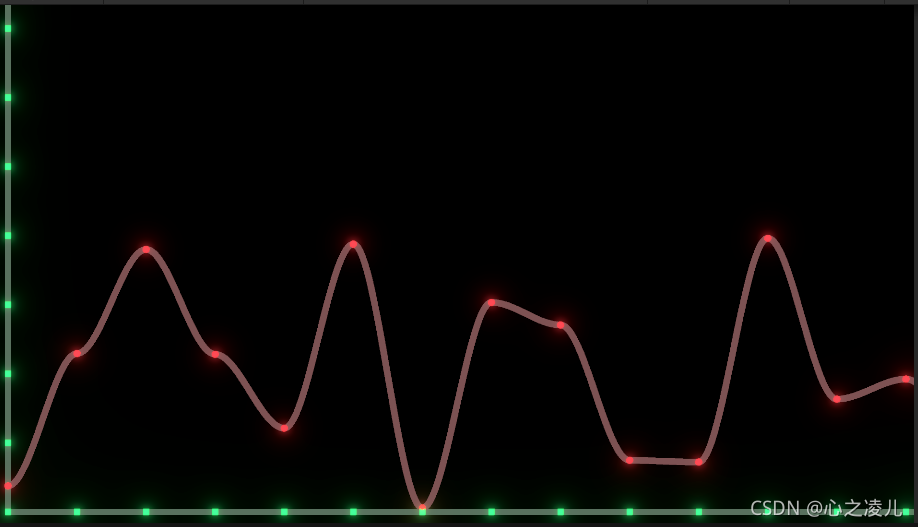
为了更好理解这两个插值函数，先通过可视化代码看一下生成的曲线效果，首先是 $3t^{2}-2t^{3}$ 插值函数的显示效果，我们简单的修改一下求插值方法，更新画线插值处的代码：

 	//相邻两个整数点位之间插值获取其他位置数值
    void CreateLine()
    {
   
        int posIndex = 0;
        int interIndex;
        line.positionCount = interIndexMax * (points.Count - 1);
        for (int i = 1; i < points.Count; i++)
        {
   
            interIndex = 0;
            while (interIndex< interIndexMax)
            {
   
            	interIndex++;
                float posY = Mathf.Lerp(points[i - 1].y, points[i].y, InterpolationCalculation(interIndex / (float)interIndexMax));
                Vector3 pos = new Vector3(i - 1 + interIndex / (float)interIndexMax, posY, 0);
                line.SetPosition(posIndex, pos);
                posIndex++;
            }
        }
    }

    //插值函数的计算
    float InterpolationCalculation(float num)
    {
   
        return 3*Mathf.Pow(num, 2)-2*Mathf.Pow(num,3);
    }

在上面的代码中，简单的封装了一个函数计算公式，然后通过线性插值做了一个从两个整数点的区间范围到（0，1）之间的映射，最终得到的曲线为：
在这里插入图片描述

与线性插值，整条曲线明显平滑了许多，并且由于插值函数 $3t^{2}-2t^{3}$ 在x取值0和1时对应的坐标点斜率为0，所以最终求得的插值曲线在整数点呈连续状态, 但是在整数点看起来依旧尖锐，所以在最新Perlin Noise生成算法中插值函数被更换为 $6t^{5}-15t^{4}+10t^{3}$

Unity 柏林噪声

悦读