GAN的基本结构和初步理解
记笔记是为了将已经了解的知识从个例抽象出来,以便将其运用到普遍情况并且记下易错点、难点,方便回忆
1. 基本结构
一个GAN(生成对抗网络)的主要结构由一个生成模型G(enerator)和一个判别模型D(iscriminator)组成
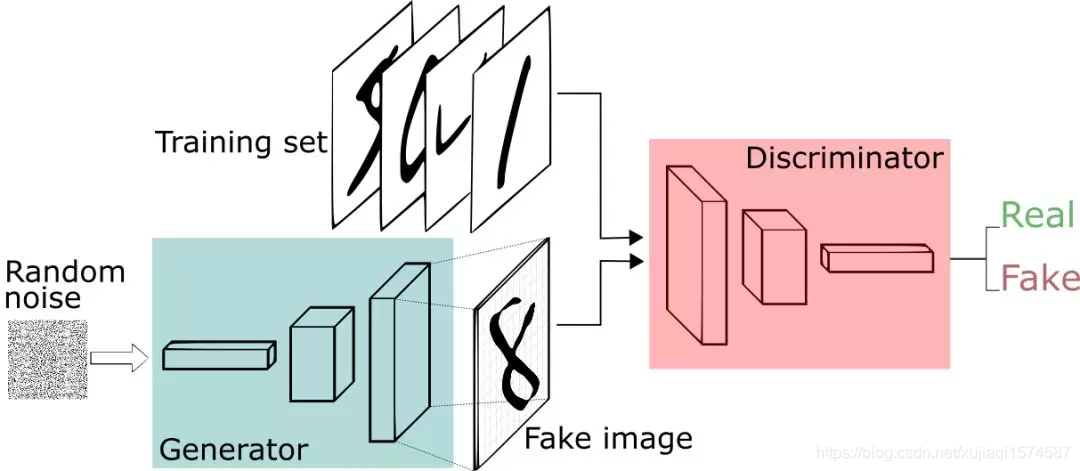
结构如图:
(Figure 1.1)GAN的基本结构
生成模型G:可以是神经网络或者其他方式拟合出的一个函数,给定输入,负责生成整个GAN所需的输出
判别模型D:可以当作一个判断输入真假的二分类器,也是一个函数
2. 基本原理
GAN中采取的是二者博弈的思想,由生成模型G不断生成输出并与训练集一同输入进判别模型D中进行判断,然后优化学习,
生成模型G和判别模型D二者相互博弈,共同学习从而达到最优(生成模型生成的输出与训练集放入后判别模型输出为0.5,即无法判定输入是否为真实数据)
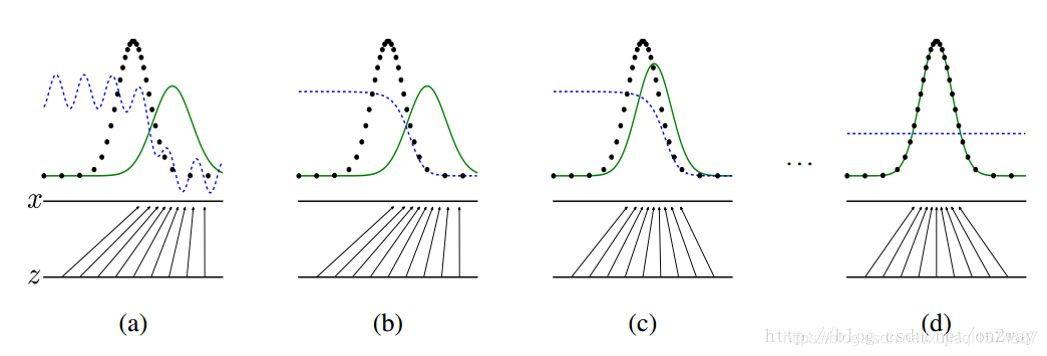
(Figure 2.1)上图中为生成模型将给定的输入X原本服从均匀分布学习至服从正态分布的过程
> 图源见水印,我也忘了人家地址了我
3. 深入理解
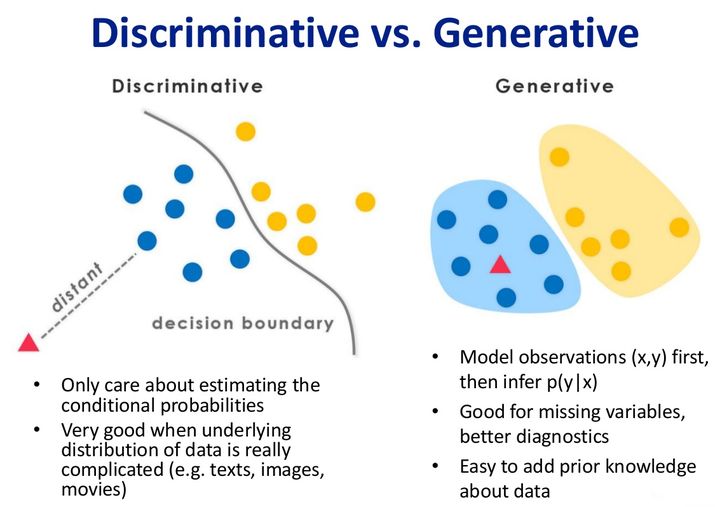
3.1 两种模型的区别
| 区分 | 判别模型 | 生成模型 |
|---|---|---|
| 功能 | 需要先训练的模型,能够判别这个数据是否来自真实数据集 ,返回值大于0.5就为真,小于0.5为假, 相当于是生成模型的标尺 | 在判别模型训练好后训练的模型, 能够在给定输入的情况下得到一定的输出, 然后送给判别模型判断后返回误差值, 从而达到让自身学习的目的模型 |
| 训练方法 | 将生成模型生成的假样本集的标签设置为0, 给定的训练集标签设置为1,即相当于训练一个简单的二分类器 不断给出生成模型的输出的误差,从而可以让 生成模型不断被优化,自己学习所需要的分布 | 训练好判别模型后,将生成的样本标签也设置为1, 从而让判别器自己去判断它的概率,从而得到误差并且学习, 自身相当于一个有监督的机器学习,让其继续学习下去。 让生成样本越来越 接近判别器想要的程度 |
| 概率分布类型 | 条件概率分布(原理是在y条件下,x发生的概率有多大) | 联合概率分布(x和y同时发生的概率) |
| 含义 | 在已知真实样本的条件下,本样本是真实样本的概率为多少 | 输入x和输出y(即输出样本)同时符合要求的概率为多大 |
| 优点 | 计算边缘分类方面比较灵活,学习简单,性能较好 | 收敛速度快,可以学习分布,应对隐变量 |
| 缺点 | 不能获得概率分布(密度) | 学习复杂,分类性能差 |
| 抽象形容 | 就相当于你不能将低维物体转向高维一样, 计算分类就像是计算出两类样本中间的线 | 这里的分布较之于判别模型就是高维物体,概率分布较为清晰, 就好比是平面形状而不是线,所以它能转换为判别式模型,而反之不能 |
(Figure 3.1) 两种分布的含义
3.2 模型的目标与原理
原始论文中,GAN的目标函数为:
min
G
max
D
V
(
D
,
G
)
=
E
x
∼
p
d
a
t
a
(
x
)
[
log
D
(
x
)
]
+
E
z
∼
p
z
(
z
)
[
log
(
1
−
D
(
G
(
z
)
)
)
]
\min _{G} \max _{D} V(D, G)=\mathbb{E}_{\boldsymbol{x} \sim p_{\mathrm{data}}(\boldsymbol{x})}[\log D(\boldsymbol{x})]+\mathbb{E}_{\boldsymbol{z} \sim p_{\boldsymbol{z}}(\boldsymbol{z})}[\log (1-D(G(\boldsymbol{z})))]
minGmaxDV(D,G)=Ex∼pdata(x)[logD(x)]+Ez∼pz(z)[log(1−D(G(z)))]
其中:z是先验概率分布Pz的一个噪声样本,x是一个服从特定分布Pdata的一个真实人脸头像。并且,在收敛性上,合成的图像分布Pg与Pdata是相同的
函数优化的大体目标是:
生成函数G试图捕捉底层的数据密度,混淆判别函数D,而D的优化过程则是为了实现自然人脸图像与G生成的假人脸图像的可分辨性和区分性(真假样本的不同以及哪个是真实样本,哪个是生成样本)。G和D都可以用多层感知器(Multi-Layer Perceptron, MLP)等神经网络拟合。
函数理解:
E x ∼ p d a t a ( x ) [ log D ( x ) ] \mathbb{E}_{\boldsymbol{x} \sim p_{\mathrm{data}}(\boldsymbol{x})}[\log D(\boldsymbol{x})] Ex∼pdata(x)[logD(x)]减少D(x)的误差,x服从Pdata分布,即给定数据集(训练集)中的人脸分布,log(D(x))保证了正相关的同时极大减少了量纲带来的影响
同理, E z ∼ p z ( z ) [ log ( 1 − D ( G ( z ) ) ) ] \mathbb{E}_{\boldsymbol{z} \sim p_{\boldsymbol{z}}(\boldsymbol{z})}[\log (1-D(G(\boldsymbol{z})))] Ez∼pz(z)[log(1−D(G(z)))]中D(G(z))的意思是将G函数从z生成的人脸图像放入D中z服从Pz分布,即输入的分布,减少1-D(G(z))就是增大判别器D判断错G生成的图像的误差,也就是说既要增大判别器D的识别人脸能力,还要慢慢地能够增大D判断错G生成的图像,也就是增强了G生成的像是给定训练集的能力,让G生成的图像越来越“真实”
3.3 总结
能够增大D判断错G生成的图像,也就是增强了G生成的像是给定训练集的能力,让G生成的图像越来越“真实”
3.3 总结
以上,就是对于最基本的GAN的结构的理解,大体上就是如此,但要对其数学统计原理进行理解还需要更深的数学基础,这在后面相信我终究会实现