目录
前言
最近在学习高博的《视觉slam十四讲》,在实践部分感觉手写视觉里程计的部分的代码还是比较有学习意义的,想做个源码分析,一来学习其中使用的c++编程技巧,二是对其中用到的一些算法查漏补缺,或者说温故知新,其实是从头开始。
一、algorithm.h文件源码分析
文件源码如下:
//
// Created by gaoxiang on 19-5-4.
//
#ifndef MYSLAM_ALGORITHM_H
#define MYSLAM_ALGORITHM_H
// algorithms used in myslam
#include "myslam/common_include.h"
namespace myslam {
/**
* linear triangulation with SVD
* 线性三角测量
* @param poses poses,
* @param points points in normalized plane
* @param pt_world triangulated point in the world
* @return true if success
*/
inline bool triangulation(const std::vector<SE3> &poses,
const std::vector<Vec3> points, Vec3 &pt_world) {
// typedef Eigen::Matrix<double, Eigen::Dynamic, Eigen::Dynamic> MatXX;
MatXX A(2 * poses.size(), 4);
// typedef Eigen::Matrix<double, Eigen::Dynamic, 1> VecX;
VecX b(2 * poses.size());
b.setZero();
for (size_t i = 0; i < poses.size(); ++i) {
Mat34 m = poses[i].matrix3x4(); // 提取A中前3*4的矩阵
// block块运算
A.block<1, 4>(2 * i, 0) = points[i][0] * m.row(2) - m.row(0);
A.block<1, 4>(2 * i + 1, 0) = points[i][1] * m.row(2) - m.row(1);
}
// 貌似当A不是动态定义的matrix时,后面参数要改成 ComputeFullU和ComputeFullV
auto svd = A.bdcSvd(Eigen::ComputeThinU | Eigen::ComputeThinV);
pt_world = (svd.matrixV().col(3) / svd.matrixV()(3, 3)).head<3>();
if (svd.singularValues()[3] / svd.singularValues()[2] < 1e-2) {
// 解质量不好,放弃
return true;
}
return false;
}
// converters
inline Vec2 toVec2(const cv::Point2f p) { return Vec2(p.x, p.y); }
} // namespace myslam
#endif // MYSLAM_ALGORITHM_H1.1 三角测量原理
已知相机的参数P_i和匹配点 x_i,来恢复三维点的坐标 X
设,第i个相机的投影矩阵:
对应在第i个相机中的图像坐标为:
求空间的三维点坐标:![X=\left[X_w,Y_w,Z_w,1\right]^T](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT9YJTNEJTVDbGVmdCU1QlhfdyUyQ1lfdyUyQ1pfdyUyQzElNUNyaWdodCU1RCU1RVQ%3D)
根据投影方程可以得到:
上述等式两侧同时叉乘 :
根据向量叉积的运算,展开得:
上式中第3个等式是,前两个等式的线性组合,因此可以去掉,整理可得:
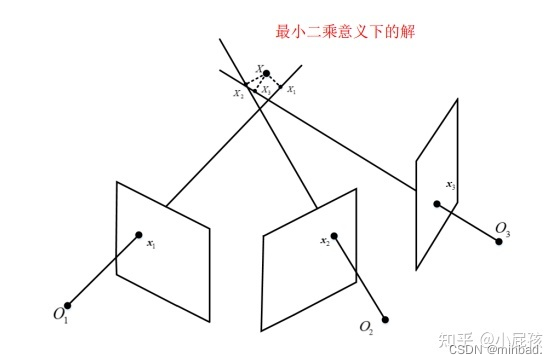
其中P_{ij}表示第i个投影矩阵的第j行。1个观测点提供2个约束,X有3个自由度,求解该方程至少2对点(从几何意义上解释,两条射线相交可确定空间中的一个三维点)。
本部分来源:什么是三角测量法? - 小屁孩的回答 - 知乎 https://www.zhihu.com/question/27719009/answer/2363041390
1.2 svd解齐次线性方程
对于齐次线性方程组Ax=0 ,必然有零解 x=0 ,但通常我们关心的是非零解,因此一般写成如下带约束条件的最小二乘问题:
设 A的一般性SVD分解为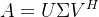
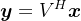
又由于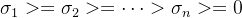
![\boldsymbol{y}\stackrel{\mathbb{D}}{\underline{{s}}}[0,0,\cdots,1]^{H}](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lNUNib2xkc3ltYm9sJTdCeSU3RCU1Q3N0YWNrcmVsJTdCJTVDbWF0aGJiJTdCRCU3RCU3RCU3QiU1Q3VuZGVybGluZSU3QiU3QnMlN0QlN0QlN0QlNUIwJTJDMCUyQyU1Q2Nkb3RzJTJDMSU1RCU1RSU3QkglN0Q%3D)
此时:
总结
未完待续……
![x_{i}=\left[u_{i},v_{i},1\right]^{T}](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT94XyU3QmklN0QlM0QlNUNsZWZ0JTVCdV8lN0JpJTdEJTJDdl8lN0JpJTdEJTJDMSU1Q3JpZ2h0JTVEJTVFJTdCVCU3RA%3D%3D)
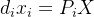
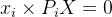
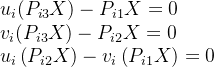
![\left[\begin{matrix}{u_{i}P_{i3}-P_{i1}}\\ {v_{i}P_{i3}-P_{i2}}\\ \end{matrix}\right]X=0](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lNUNsZWZ0JTVCJTVDYmVnaW4lN0JtYXRyaXglN0QlN0J1XyU3QmklN0RQXyU3QmkzJTdELVBfJTdCaTElN0QlN0QlNUMlNUMlMjAlN0J2XyU3QmklN0RQXyU3QmkzJTdELVBfJTdCaTIlN0QlN0QlNUMlNUMlMjAlNUNlbmQlN0JtYXRyaXglN0QlNUNyaWdodCU1RFglM0Qw)
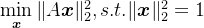
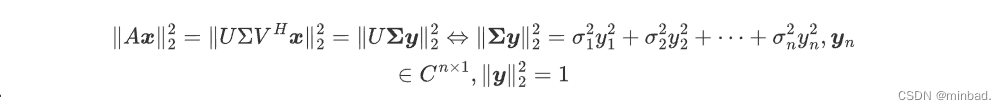
![\boldsymbol{x}=V\boldsymbol{y}=[\boldsymbol{v}_1,\boldsymbol{v}_2,\cdots,\boldsymbol{v}_n]\begin{pmatrix}0\\ 0\\ \vdots\\ 1\end{pmatrix}=\boldsymbol{v}_n](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lNUNib2xkc3ltYm9sJTdCeCU3RCUzRFYlNUNib2xkc3ltYm9sJTdCeSU3RCUzRCU1QiU1Q2JvbGRzeW1ib2wlN0J2JTdEXzElMkMlNUNib2xkc3ltYm9sJTdCdiU3RF8yJTJDJTVDY2RvdHMlMkMlNUNib2xkc3ltYm9sJTdCdiU3RF9uJTVEJTVDYmVnaW4lN0JwbWF0cml4JTdEMCU1QyU1QyUyMDAlNUMlNUMlMjAlNUN2ZG90cyU1QyU1QyUyMDElNUNlbmQlN0JwbWF0cml4JTdEJTNEJTVDYm9sZHN5bWJvbCU3QnYlN0Rfbg%3D%3D)