上一篇文章「 排序算法 」已经整体的把排序算法的分类和评估方法介绍了一下,今天起咱们就开始依次介绍一下各种排序算法的原理和特性。咱们就从最容易理解的「 冒泡排序 」开始吧。
一、「 冒泡排序 」是什么?
冒泡排序是一种交换排序,它的思路就是在待排序的数据中,两两比较相邻元素的大小,看是否满足大小顺序的要求,如果满足则不动,如果不满足则让它们互换。然后继续与下一个相邻元素的比较,一直到一次遍历完成。一次遍历的过程就被成为一次冒泡,一次冒泡的结束至少会让一个元素移动到了正确的位置。所以要想让所有元素都排序好,一次冒泡还不行,我们得重复N次去冒泡,这样最终就完成了N个数据的排序过程。
通过上面的描述,可以看出来冒泡排序在代码实现层面不就是两层循环嘛,哈哈。
下面举例:
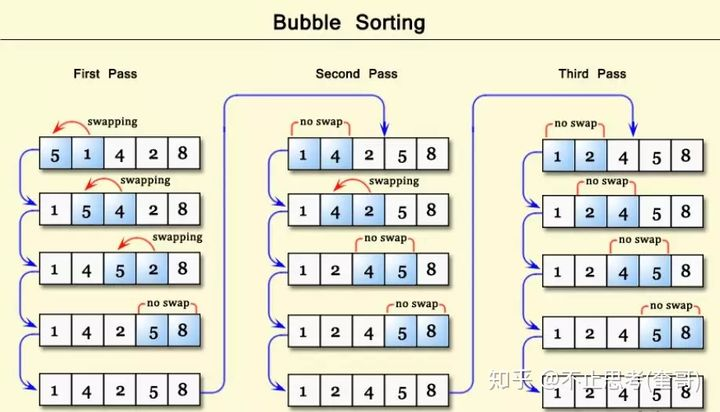
如图,这是针对数组:5,1,4,2,8 采用冒泡排序进行从小到大的排列,上图中分别进行了三次冒泡后完成了整个排序过程。
先看第一次冒泡:
- 从数组的第0位开始,比较5和1,发现5>1,交换位置,交换后数组为:1,5,4,2,8
- 继续下一个元素的比较,比较5和4,发现5>4,交换位置,交换后数组为:1,4,5,2,8
- 继续下一个元素的比较,比较5和2,发现5>2,交换位置,交换后数组为:1,4,2,5,8
- 继续下一个元素的比较,比较5和8,发现5<8,不用交换,数组保持不变:1,4,2,5,8
- 继续下一个元素的比较,发现没有元素了,不用比较了,数组在第一轮冒泡排序后的最终状态就是:1,4,2,5,8 了,此时 元素 8 已经到了正确的位置,其它元素位置还是不对,需要循环进行下一轮冒泡。
第二次冒泡和第三次冒泡的原理与第一次冒泡一样,这里就不描述了,直接看上图,图中有清晰的流程标注。
我们在写冒泡排序的时候,有两个事项需要注意:
- 冒泡的次数可以减少:
理论上如果数组有N个元素,且这N个元素完全是倒序的话,我们需要进行N次冒泡才可以完成排序工作,但是通过上面的示例可以发现,上述数组有5位,但是我们只进行了三次冒泡就完成了,原因就是因为数组中有些元素之前就已经是有序的了。那我们怎么判断该用几次冒泡操作呢?
冒泡停止的条件就是:当某次冒泡操作全程都无需进行元素交换,就说明此时这个数组已经达到了完全有序状态了,无需再进行下一次冒泡了。
上图中的第三次冒泡过程中,没有一次需要元素交换的,因此就不需要进行第四次冒泡了。
在写代码的时候,需要使用一个变量来做好标记,下面我们来写一个冒泡代码:
算法题:对数组arr进行从小到大的排序,假设数组arr不为空,arr的长度为n
思路:有两种方式都可以,一个是从数组前往后冒泡,将最大的元素移动到最后面,另一种方式是从数组的后面往前冒泡,将最小的元素移动到最前面。
public class BubbleSort {
// 数组int[] arr,长度 n,要求从左到右按照从小到大的顺序排序
/**
* 从前往后冒泡
* 上面的图片就是这种形式
* */
public void bubbleSort1(int[] arr, int n) {
for (int i = 0; i < n; i++) {
// flag是用来标记本次冒泡中是否有元素交换,用来决定冒泡停止条件的
boolean flag = false;
//排了一边之后,因为是大的往后移动,第一次排序最后一位肯定确定了是最大值
//第二次排序后两位肯定确定了最大值,因此不需要再判断,j < n-i-1
for (int j = 0; j < n-i-1; j++) {
// 从第一个开始,相邻元素两两比较,如果前一个比后一个大则交换
if (arr[j] > arr[j+1]) {
int temp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = temp;
flag = true; // 如果有元素交换了,就设置为true
}
}
// 一次冒泡下来没有元素交换,就提前退出
if (!flag) break;
}
}
/**
* 从后往前冒泡
* */
public static void bubbleSort2(int[] arr,int n) {
for (int i = 0; i < n; i++) {
//
boolean flag = false;
for (int j = n-i-1 ; j > i; j--) {
//
if (arr[j-1] > arr[j]) {
int temp = arr[j];
arr[j] = arr[j-1];
arr[j-1] = temp;
flag = true;
}
}
if (!flag) break;
}
}
}- 冒泡一定是对比相邻元素:
冒泡排序的原则很简单,就是相邻的两两对比然后判断是否交换。但其中有个新人很容易疏忽的就是“相邻”这个词,我们在循环中对比的元素一定是要相邻的,不能拿着某个元素依次对比数组中的所有元素(比如先拿数组0位元素依次对比其它元素,将最小的置换到第0位,然后再拿数组1位元素依次对比剩下所有元素,将剩下元素最小的置换到第1位,依次循环),虽然这种方式也能最后排序也能完成,但是效率非常的低。为什么这种方式效率低呢?
因为这种方式每一次元素交换,虽然都将当前最小的元素移动到了正确的位置,但是对于其它元素的位置没有半点改进,甚至会由于交换导致其它比较小的元素这次遍历中移动到后面。
而采用“相邻元素两两对比”的方式,每次冒泡不仅能将一个元素移动到正确的位置,还能附带着对其它元素的位置有改进。
二、「 冒泡排序 」的性能怎么样?
我们按照前一篇文章讲到的排序算法评估方法来对「 冒泡排序 」进行一下评估:
- 时间复杂度:
冒泡排序原理就是在两层循环里进行两两对比嘛,所以简单去思考的话,一般情况下的时间复杂度就是O(n*n)了。但是实际还是得看数据情况,如果待排序的数据本身就是有序的,其实我们只需要做依次冒泡就完成了(也就是一次循环),那么此时就是最好时间复杂度:O(n),如果待排序的数据全部都是逆序的,那我们需要做 n(n-1)/2 次循环,最坏时间复杂度就是:O(n*n)了。 - 空间复杂度:
通过我们对冒泡排序原理的了解,知道冒泡排序在排序的过程中,不需要占用很多额外的空间(就是在交换元素的时候需要临时变量存一存,这里需要的额外空间开销是常量级的),因此冒泡排序的空间复杂度为O(1)了。 - 排序稳定性:
上一篇介绍过了排序算法稳定性的定义,这里不重复介绍了。对于冒泡排序而言,在做元素对比的时候,如果大小顺序不满足要求,则将它们进行交换,如果满足要求,或者元素相等,则啥都不做。可知,在元素相当的情况下,位置没有发生变化,因此它是排序稳定的。 - 算法复杂性:
冒泡排序的算法无论是其设计思路上,还是代码的编写上都不复杂,因此冒泡排序算法复杂性是比较简单的。