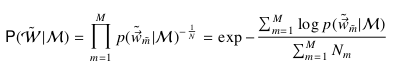为了计算LDA 的困惑度,费劲千辛万苦,终于有所收获,以此记录。
本篇文章主要介绍perplexity的计算方式,并未涉及过多的困惑度原理,想了解更多原理部分,请移步perplexity介绍
本文主要是对Perplexity per word进行困惑度计算,公式:
以下是实现代码(工具pycharm、Python3.7),分了三个部分
1.LDA的主题生成
from gensim import corpora, models
def ldamodel(num_topics):
cop = open(r'D:\360MoveData\Users\admin\Desktop\copus.txt', 'r', encoding='UTF-8')
train = []
for line in cop.readlines():
line = [word.strip() for word in line.split(' ')]
train.append(line) # list of list 格式
dictionary = corpora.Dictionary(train)
corpus = [dictionary.doc2bow(text) for text in
train] # corpus里面的存储格式(0, 1), (1, 1), (2, 1), (3, 1), (4, 1), (5, 1), (6, 1)
corpora.MmCorpus.serialize('corpus.mm', corpus)
lda = models.LdaModel(corpus=corpus, id2word=dictionary, random_state=1,
num_topics=num_topics) # random_state 等价于随机种子的random.seed(),使每次产生的主题一致
topic_list = lda.print_topics(num_topics, 10)
# print("主题的单词分布为:\n")
# for topic in topic_list:
# print(topic)
return lda,dictionary2.编辑perplexity的计算函数
import math
def perplexity(ldamodel, testset, dictionary, size_dictionary, num_topics):
print('the info of this ldamodel: \n')
print('num of topics: %s' % num_topics))
prep = 0.0
prob_doc_sum = 0.0
topic_word_list = []
for topic_id in range(num_topics):
topic_word = ldamodel.show_topic(topic_id, size_dictionary)
dic = {}
for word, probability in topic_word:
dic[word] = probability
topic_word_list.append(dic)
doc_topics_ist = []
for doc in testset:
doc_topics_ist.append(ldamodel.get_document_topics(doc, minimum_probability=0))
testset_word_num = 0
for i in range(len(testset)):
prob_doc = 0.0 # the probablity of the doc
doc = testset[i]
doc_word_num = 0
for word_id, num in dict(doc).items():
prob_word = 0.0
doc_word_num += num
word = dictionary[word_id]
for topic_id in range(num_topics):
# cal p(w) : p(w) = sumz(p(z)*p(w|z))
prob_topic = doc_topics_ist[i][topic_id][1]
prob_topic_word = topic_word_list[topic_id][word]
prob_word += prob_topic * prob_topic_word
prob_doc += math.log(prob_word) # p(d) = sum(log(p(w)))
prob_doc_sum += prob_doc
testset_word_num += doc_word_num
prep = math.exp(-prob_doc_sum / testset_word_num) # perplexity = exp(-sum(p(d)/sum(Nd))
print("模型困惑度的值为 : %s" % prep)
return prep3.主函数入口,并作图
from gensim import corpora, models
import matplotlib.pyplot as plt
import perplexity
import lda_catch
def graph_draw(topic, perplexity): # 做主题数与困惑度的折线图
x = topic
y = perplexity
plt.plot(x, y, color="red", linewidth=2)
plt.xlabel("Number of Topic")
plt.ylabel("Perplexity")
plt.show()
if __name__ == '__main__':
for i in range(20,300,1): # 多少文档中抽取一篇(这里只是为了调试最优结果,可以直接设定不循环)
print("抽样为"+str(i)+"时的perplexity")
a=range(1,20,1) # 主题个数
p=[]
for num_topics in a:
lda,dictionary =lda_catch.ldamodel(num_topics)
corpus = corpora.MmCorpus('corpus.mm')
testset = []
for c in range(int(corpus.num_docs/i)):
testset.append(corpus[c*i])
prep = perplexity.perplexity(lda, testset, dictionary, len(dictionary.keys()), num_topics)
p.append(prep)
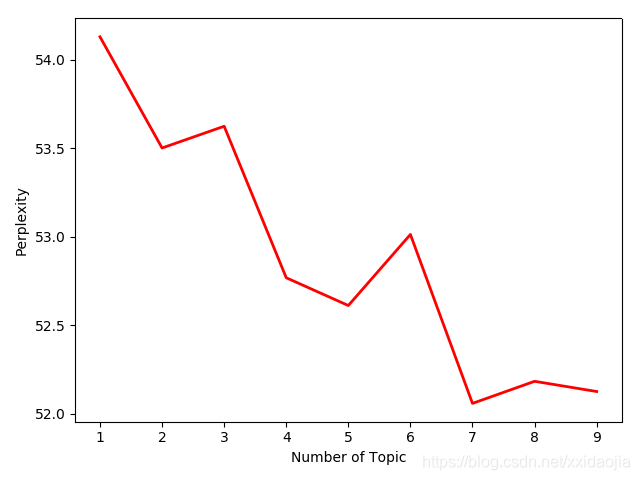
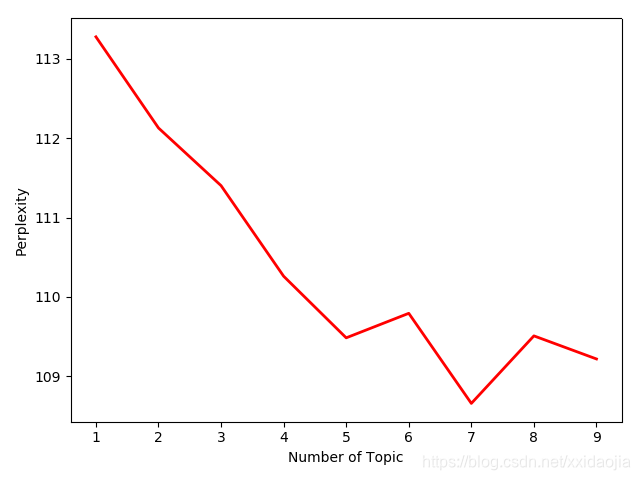
graph_draw(a,p)最终结果:(不同训练集测试部分图)
初学者对困惑度计算的了解,若有不足请指出。
参考文献: