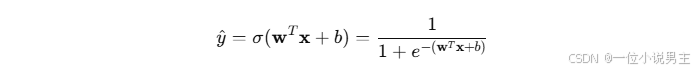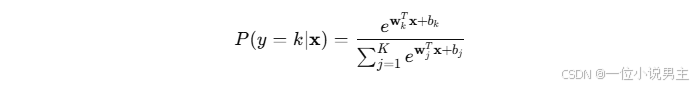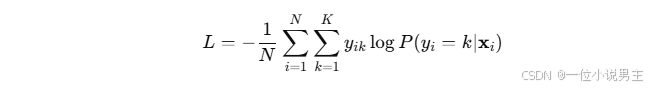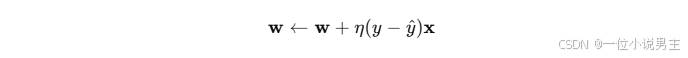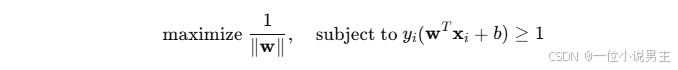引言

在机器学习中，线性分类器 是一种经典而高效的分类方法，能够在特征空间中寻找一条（或一个超平面）来区分不同类别的数据点。它是现代机器学习模型的基石，同时为许多复杂模型（如神经网络）奠定了理论基础。本文将详细解析四种常见的线性分类器——Logistic 回归、Softmax 回归、感知器和支持向量机（SVM），以帮助读者深入理解其原理、应用及优劣点。

一、Logistic 回归：二分类问题的经典之作

1.1 什么是 Logistic 回归？

Logistic 回归 是一种专注于二分类问题的线性分类器。尽管名字带有“回归”，其本质是分类模型。通过对输入特征进行线性变换，并通过一个 Sigmoid 函数 转化为概率值，最终进行分类决策。

数学表达：
假设输入样本为 x∈Rd，其预测函数为：

其中，σ(z)是 Sigmoid 函数，w和b是模型参数。 

1.2 损失函数及优化

Logistic 回归通过最小化 对数似然损失函数 来学习模型参数：

• yi​∈{0,1} 表示真实类别。
• y^i是模型预测的类别概率。

1.3 优点与局限性

• 优点：
  1. 简单高效，适合小规模线性可分的数据。
  2. 输出概率值，解释性强。
• 局限性：
  1. 对非线性问题表现欠佳。
  2. 特征独立性假设可能导致欠拟合。

实战案例

使用 Python 和 scikit-learn 实现 Logistic 回归：

from sklearn.datasets import make_classification
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

# 创建数据集
X, y = make_classification(n_samples=1000, n_features=20, random_state=42)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 训练模型
model = LogisticRegression()
model.fit(X_train, y_train)

# 测试并评估
y_pred = model.predict(X_test)
print(f"Accuracy: {accuracy_score(y_test, y_pred):.2f}")

二、Softmax 回归：多分类的自然扩展

2.1 什么是 Softmax 回归？

当 Logistic 回归扩展到多分类问题时，成为 Softmax 回归。它通过 Softmax 函数将线性变换映射到概率分布，从而支持多类别分类任务。

数学表达：
给定输入 x，类别概率为：

其中，K是类别数，wk和 bk是类别 k对应的参数。 

2.2 损失函数及优化

Softmax 回归采用 交叉熵损失：

其中，yik是类别 k的 one-hot 编码。 

2.3 优点与局限性

• 优点：
  1. 适用于多分类问题。
  2. 模型输出是类别概率分布。
• 局限性：
  1. 仅能处理线性边界。
  2. 容易受类别分布不均影响。

实战案例

实现 Softmax 回归：

from sklearn.datasets import make_classification
from sklearn.linear_model import LogisticRegression

# 创建数据集
X, y = make_classification(n_samples=1000, n_features=20, n_classes=3, random_state=42)

# 训练 Softmax 回归
model = LogisticRegression(multi_class='multinomial', solver='lbfgs')
model.fit(X, y)

# 测试分类
y_pred = model.predict(X)
print(f"Accuracy: {model.score(X, y):.2f}")

三、感知器：最早的线性分类器

3.1 感知器的基本概念

感知器（Perceptron） 是一种线性分类算法，由 Rosenblatt 于 1958 年提出。它是神经网络的雏形，使用简单的规则调整权重，直到找到一个分隔类别的超平面。

更新规则：

• y 是真实标签，y^是预测标签。
• η是学习率。

3.2 优点与局限性

• 优点：实现简单，收敛速度快。
• 局限性：
  1. 仅适用于线性可分数据。
  2. 容易陷入无解状态。

四、支持向量机（SVM）：强大的分类器

4.1 什么是支持向量机？

支持向量机（SVM） 是一种强大的线性分类器，旨在找到一个最大化分类边界的超平面。

数学目标：

4.2 优点与局限性

• 优点：
  1. 能很好处理高维数据。
  2. 通过核函数扩展到非线性问题。
• 局限性：
  1. 对大规模数据不适用。
  2. 参数调节复杂。

结语

线性分类器简单却强大，适用于从基础到进阶的各种学习场景。Logistic 和 Softmax 回归适合初学者快速入门，而感知器和支持向量机则是理解现代分类器的关键。选择哪种方法取决于数据特征和任务需求，掌握这些方法后，你将拥有更强大的分类工具库！