本期参考:区间 DP:最长回文子序列【基础算法精讲 22】_哔哩哔哩_bilibili
ps:笔记中的代码按本人理解整理,重思路,对比原视频中的代码稍有改动
【如果笔记对你有帮助,欢迎关注&点赞&收藏,收到正反馈会加快更新!谢谢支持!】
题目1:最长回文子序列
- 思路:用首尾来表示一个序列区间,处理“字符串A = 首 + 字符串B + 尾"
- 拆解:
- 回文串的两种情况:
- 一个字符
- 回文串A = x + 回文串B + x (其中x为任意字符),比如'aba' 其中x='a'
- 题目要求最长子回文序列长度(字符串可以任意删字符来变成回文串,只要留下的回文串顺序不变)Eg: 'aba', 'abca', 'abac','abcca' 这四个str留下的回文串为'aba',所以最长子回文序列都等于3。
因为 字符串A包含回文串A, 字符串B包含回文串B(比如'abac'包含'aba'),所以下面用字符串讨论。 - 两种处理情况(用“result_A” 表示 字符串A的最长回文子序列)
- 字符串A = x + 字符串B + x 【result_A = result_B + 2】
- 字符串A = x + 字符串B + y (x ≠ y) 【result_A = max{result_xB, result_By}】
(取 “x + 字符串B” 和 “字符串B + y” 的最大值作为 字符串A的最长回文子序列)
- 需要从小区间处理到大区间,因为 len(字符串A) ≧ len(字符串B),要先拿到字符串B对应的值,再处理字符串A
- 回文串的两种情况:
- 代码:
class Solution: def longestPalindromeSubseq(self, s: str) -> int: n = len(s) dp = [[0]*n for _ in range(n)] #需要二维dp(n*n)分别表示首尾 # i表示首, j表示尾,dp[i][j]表示i到j这个区间的最长子回文序列长度 # 先确认区间,再处理区间 for j in range(n): dp[j][j] = 1 # 一个字符串的情况,也是长度为1的回文串 for i in range(j-1, -1, -1): # i要倒序是因为dp[i]要从dp[i+1]转移过来 if s[i] == s[j]: # 字符串A(i为首,j为尾) = x + 字符串B(i+1为首,j-1为尾) + x dp[i][j] = dp[i+1][j-1] + 2 else: # 字符串A = x + 字符串B + y (x ≠ y) dp[i][j] = max(dp[i+1][j], dp[i][j-1]) return dp[0][n-1] # 返回一整个字符串对应的值
题目2: 多边形三角剖分的最低得分
1039. 多边形三角剖分的最低得分 - 力扣(LeetCode)
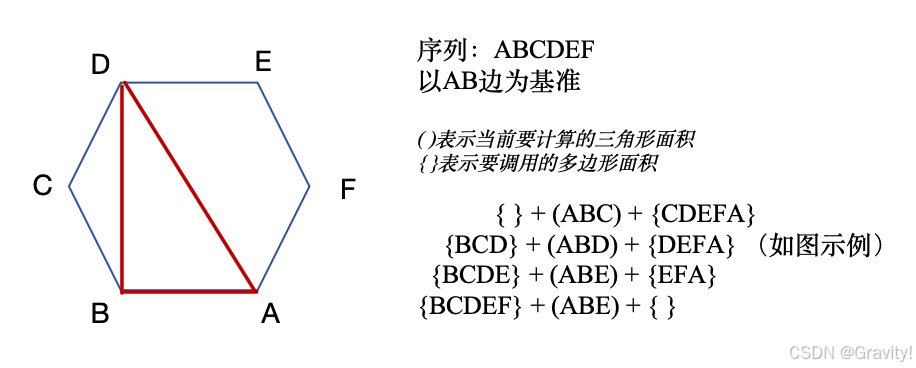
- 思路:用首尾来表示一个序列区间,处理“多边形A = 多边形B + 首尾组成的边"
- 拆解
- 从小区间(三角形)处理到大区间(多边形),因为要调用的值得是已经计算好的,上图例子要计算多边形{BCDEF},得先知道多边形{BCDE},再先要知道{BCD}
- 代码
class Solution: def minScoreTriangulation(self, values: List[int]) -> int: n = len(values) # n边形 dp = [[0]*n for _ in range(n)] # 同上题 # 先确认区间[i,j],i表示首, j表示尾 for j in range(2, n): # 从三角形(第三个顶点,索引为2)开始 for i in range(j-2, -1, -1): # 要确保有个三角形(所以j-2),遍历到第一个顶点(索引为0) # 确定多边形之后,以一条边为基准,看如何分割得到的总和最小 result = inf for k in range(i+1, j): # 以ij这条边为基准,三角形的另一个顶点从i+1遍历到j-1 result = min(result, values[i]*values[j]*values[k] + dp[i][k] + dp[k][j]) dp[i][j] = result return dp[0][n-1]