第26天,回溯part04,昨天休息复习总结回溯内容,💪(ง •_•)ง💪
目录
491.递增子序列
文档讲解:代码随想录递增子序列
视频讲解:手撕递增子序列
题目:
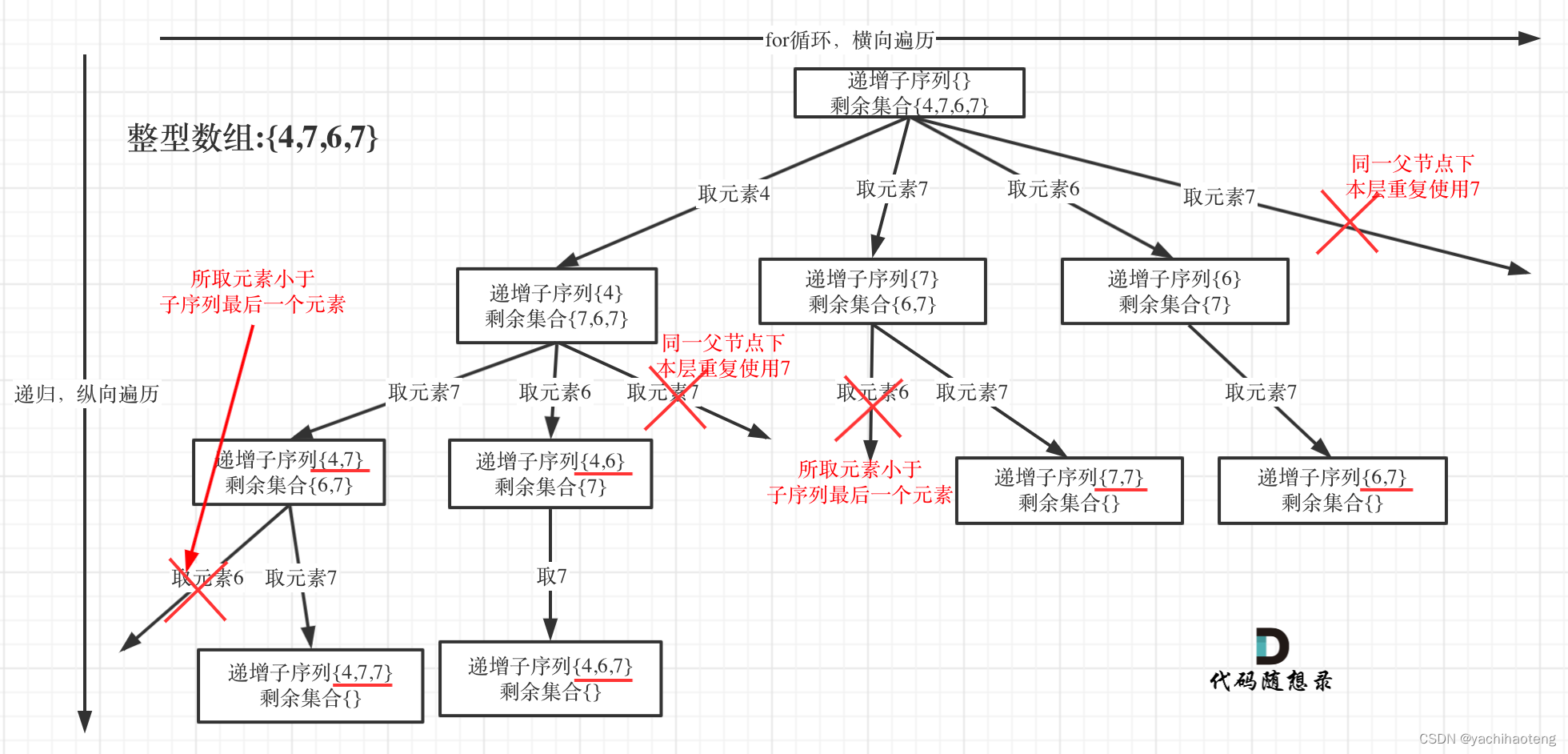
学习:本题同属于子集问题,但不同的在于给了多个限制:1.子序列必须包含两个元素以上;2.子序列必须是递增的;3.不能对数组进行排序,即不能改变各元素之间的位置关系。
同时本题还需要进行去重,由于不能对数组进行排序,因此不能采用之前的去重办法,可以通过设置一个哈希表的方式进行去重。
代码:
//时间复杂度O(n*2^n)
//空间复杂度O(n)
class Solution {
public:
vector<vector<int>> result; //返回数组
vector<int> path; //记录路径
//确定返回值和参数列表,在返回数组中直接进行操作所以不需要返回值,设置startindex确定每一层遍历范围
void backtracking (vector<int>& nums, int startindex) {
//收取路径大于1的节点
if(path.size() > 1) {
result.push_back(path);
}
//确定返回条件(在子集问题中可以不写)因为当startindex==nums.size()时,不会进入下面的循环
if(startindex == nums.size()) {
return;
}
//确定单层递归逻辑
unordered_set<int> used; //使用哈希表记录已经使用的数字
for(int i = startindex; i < nums.size(); i++) {
//查找当前遍历的数字是否符合要求: 1.当前数字是否大于path中最后一个数字;2.当前数字是否没有遍历过
if(!path.empty() && nums[i] < path.back() || (used.find(nums[i]) != used.end())) {
continue; //进行下一轮循环
}
used.insert(nums[i]);
//复合我们需要的数字条件
path.push_back(nums[i]);
backtracking(nums, i + 1);
path.pop_back(); //回溯
}
}
vector<vector<int>> findSubsequences(vector<int>& nums) {
backtracking(nums, 0);
return result;
}
};注意:本题规定了数值的范围在[-100,100]之间,数量一定且有序,因此本题也可以使用数组作为哈希表,能够提高算法效率。程序运行的时候对unordered_set 频繁的insert,unordered_set需要做哈希映射(也就是把key通过hash function映射为唯一的哈希值)相对费时间,而且每次重新定义set,insert的时候其底层的符号表也要做相应的扩充,也是费事的。
代码:
class Solution {
public:
vector<vector<int>> result; //返回数组
vector<int> path; //记录路径
//确定返回值和参数列表,在返回数组中直接进行操作所以不需要返回值,设置startindex确定每一层遍历范围
void backtracking (vector<int>& nums, int startindex) {
//收取路径大于1的节点
if(path.size() > 1) {
result.push_back(path);
}
//确定返回条件(在子集问题中可以不写)因为当startindex==nums.size()时,不会进入下面的循环
if(startindex == nums.size()) {
return;
}
//确定单层递归逻辑
int used[201] = {0}; //使用数组来记录数字是否使用过,因为题干规定数字在[-100, 100]之间。
for(int i = startindex; i < nums.size(); i++) {
//查找当前遍历的数字是否符合要求: 1.当前数字是否大于path中最后一个数字;2.当前数字是否没有遍历过
if(!path.empty() && nums[i] < path.back() || (used[nums[i] + 100] == 1)) {
continue; //进行下一轮循环
}
used[nums[i] + 100] = 1;
//复合我们需要的数字条件
path.push_back(nums[i]);
backtracking(nums, i + 1);
path.pop_back(); //回溯
}
}
vector<vector<int>> findSubsequences(vector<int>& nums) {
backtracking(nums, 0);
return result;
}
};46.全排列
文档讲解:代码随想录全排列
视频讲解:手撕全排列
题目:
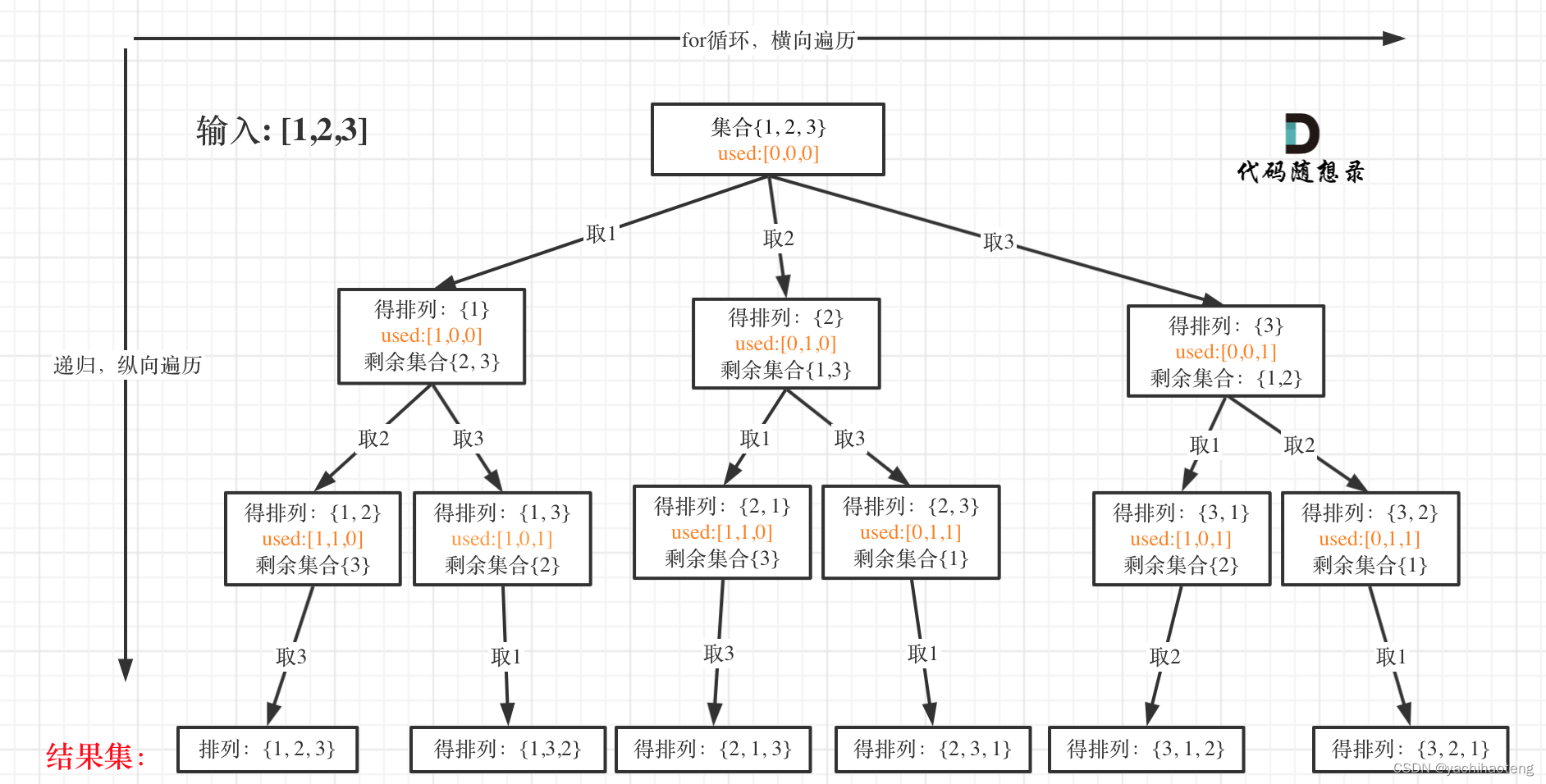
学习:回溯算法解决第四类排列问题,排列问题的特点在于:1.在叶子结点收获结果;2.每层循环需从i = 0开始。因为对于排列问题来说[1,2]与[2,1]是不同的排列方式。
基于以上两点,排列不能使用startindex确定循环范围,而是需要一个used数组来标识每个元素是否被使用。
代码:
//时间复杂度O(n!)
//空间复杂度O(n)
class Solution {
public:
//排列问题
vector<vector<int>> result; //返回数组
vector<int> path; //记录路径
//确定返回值和参数列表,在返回数组中直接操作,因此不需要返回值,与组合问题不同,排列存在顺序因此需要用一个数组来记录循环范围
void backtracking(vector<int>& nums, vector<bool>& used) {
//确定终止条件,在叶子节点处收获结果
if(path.size() == nums.size()) {
result.push_back(path);
return;
}
//确定单层递归逻辑,每次都得从0开始,由used数组来确定遍历的范围
for(int i = 0; i < nums.size(); i++) {
//如果当前数遍历过,则跳过继续往后遍历
if(used[i] == true) {
continue;
}
//如果没有遍历过,进入单层递归逻辑
used[i] = true;
path.push_back(nums[i]);
backtracking(nums, used);
//回溯
path.pop_back();
used[i] = false;
}
}
vector<vector<int>> permute(vector<int>& nums) {
//设置一个bool类型的数组,记录每次遍历过程中该数有没有被使用,事实上这种方法,在前面的去重中也能够使用
vector<bool> used(nums.size(), false);
backtracking(nums, used);
return result;
}
};47.全排列 II
文档讲解:代码随想录全排列II
视频讲解:手撕全排列II
题目:
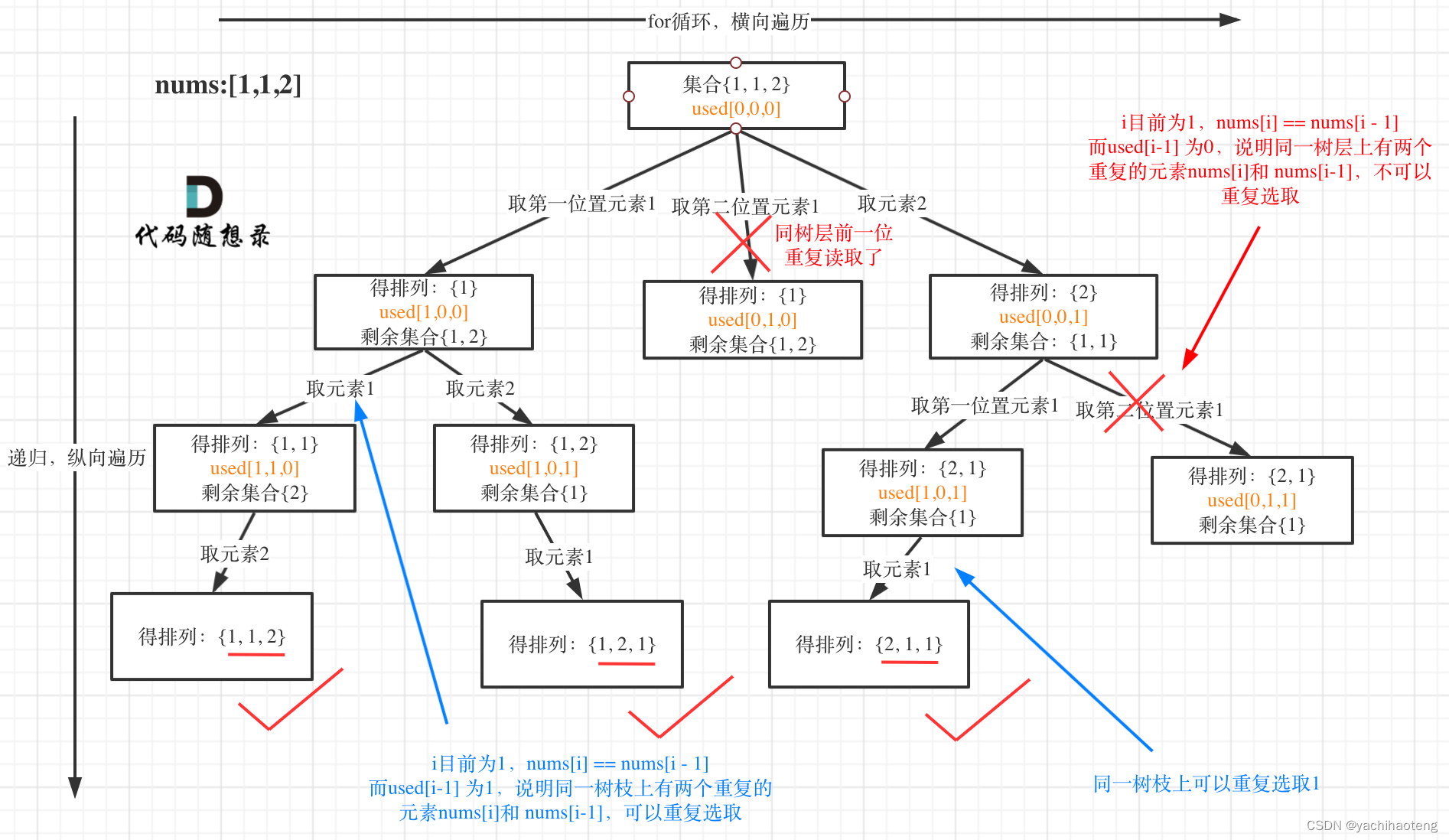
学习:本题与上一题不同在于,本题存在重复数字需要进行去重处理。由于我们设置了used数组因此可以直接使用used数组进行去重处理。原理在于:当后面出现与前面相同的数字时,且前面的数字没有被使用(used == false),此时跳过当前数字。因为for循环顺序的原因,前面的数字一定先完成所有可能性的遍历,因此遍历到后面的数字,前面的数字没有被使用,说明已经遍历完成了,这种去重也属于树层去重。(注意:使用这种方式,需要对数组先进行排序)
代码:
//时间复杂度O(n!*n)
//空间复杂度O(n)
class Solution {
public:
//本题与前一题的不同之处在于需要进行去重
vector<vector<int>> result; //返回数组
vector<int> path; //记录路径
//确定返回值和参数列表,本题与上一题不同在于去重,但使用used数组就能够进行去重处理,因此参数列表相同
void backtracking(vector<int>& nums, vector<bool>& used) {
//确定终止条件
if(path.size() == nums.size()) {
result.push_back(path);
return;
}
//确定单层递归逻辑
for(int i = 0; i < nums.size(); i++) {
//首先进行数层去重,如果后面的数和前面的数相同,且前面的数已经完成了遍历回溯为false,则跳过
if(i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {
continue;
}
//接着判断当前遍历的数是否被使用
if(used[i] == true) {
continue;
}
//进入单层递归逻辑
used[i] = true;
path.push_back(nums[i]);
backtracking(nums, used);
//回溯
path.pop_back();
used[i] = false;
}
}
vector<vector<int>> permuteUnique(vector<int>& nums) {
//建立一个used数组,记录数是否使用
vector<bool> used(nums.size(), false);
//对nums排序便于去重
sort(nums.begin(), nums.end());
backtracking(nums, used);
return result;
}
};51.N皇后
文档讲解:代码随想录N皇后
视频讲解:手撕N皇后
题目:
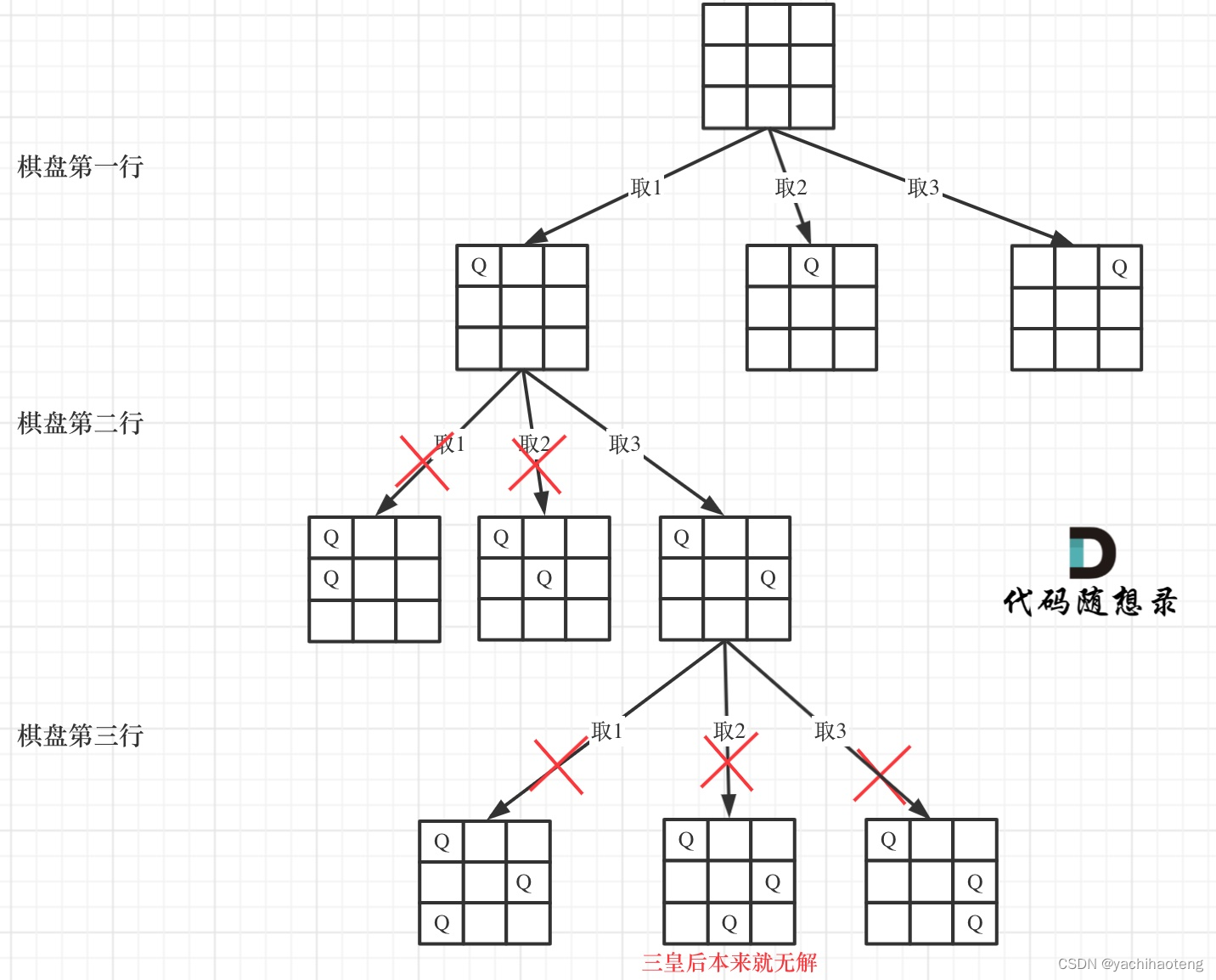
学习: 回溯算法解决第五类棋盘问题。棋盘问题的特点在于需要遍历的不再是一维数组,而是需要遍历二维数组。但本质仍是一层递归一层循环,对于本题来说每层循环需要在一行插入一个皇后,同时插入的皇后有三个约束条件:1.不能同行;2.不能同列;3.不能同斜线。基于此也可以将棋盘问题的搜索过程抽象为一棵树:
注意:棋盘问题一般也是在叶子结点收获结果,由于存在插入是否可行的判断,因此只要搜索到了树的叶子结点,就说明找到了皇后们的合理位置了。
代码:本题关键在于理解棋盘的宽度就是for循环的长度,递归的深度就是棋盘的高度,这样就可以套进回溯法的模板里了。
//时间复杂度O(n!)
//空间复杂度O(n)
class Solution {
public:
//棋盘问题
vector<vector<string>> result; //返回数组
vector<string> chessboard; //棋盘也是每一个结果
//确定返回值和参数列表,循环遍历的是列,因此加入n和当前遍历的行
void backtracking(int n, int row) {
//确定终止条件,在叶子结点收获结果,能够走到叶子结点说明一定正确
if(row == n) {
result.push_back(chessboard);
return;
}
//确定单层递归逻辑,对列进行循环遍历
for(int i = 0; i < n; i++) {
//判断当前列能不能插入皇后
if(isvalid(n, row, i)) { //如果可以的话,进行下一层递归
chessboard[row][i] = 'Q';
backtracking(n, row + 1);
//回溯
chessboard[row][i] = '.';
}
}
}
//参数分别表示n,当前行数,当前列数
bool isvalid(int n, int row, int col) {
//判断是否冲突:注意本题不需要判断行是否冲突,因为在for循环遍历过程中我们只允许一行有一个皇后
//判断列是否冲突,后面的行还没有插入皇后,所以只需要遍历到row就可以
for(int i = 0; i < row; i++) {
if(chessboard[i][col] == 'Q') return false;
}
//判断45°角位置有没有皇后
for(int i = row - 1, j = col - 1; i >= 0 && j >= 0; i--, j--) {
if(chessboard[i][j] == 'Q') return false;
}
//判断135°角位置有没有皇后
for(int i = row - 1, j = col + 1; i >= 0 && j < n; i--, j++) {
if(chessboard[i][j] == 'Q') return false;
}
return true;
}
vector<vector<string>> solveNQueens(int n) {
//对chessboard进行初始化处理
for(int i = 0; i < n; i++) {
chessboard.push_back(string(n,'.'));
}
backtracking(n, 0);
return result;
}
};37.解数独
文档讲解:代码随想录解数独
视频讲解:手撕解数独
题目:
学习:本题也属于棋盘问题,本题也需要在二维数组中插入元素,并且不断判断插入的是否合理。 但与N皇后不同的在于,本题一行不仅仅插入一个元素,而是需要插入多个元素,需要对行和列都进行遍历。因此本题一层递归不止一个循环,一层递归包含两个循环,因此本题要做的是二维递归。
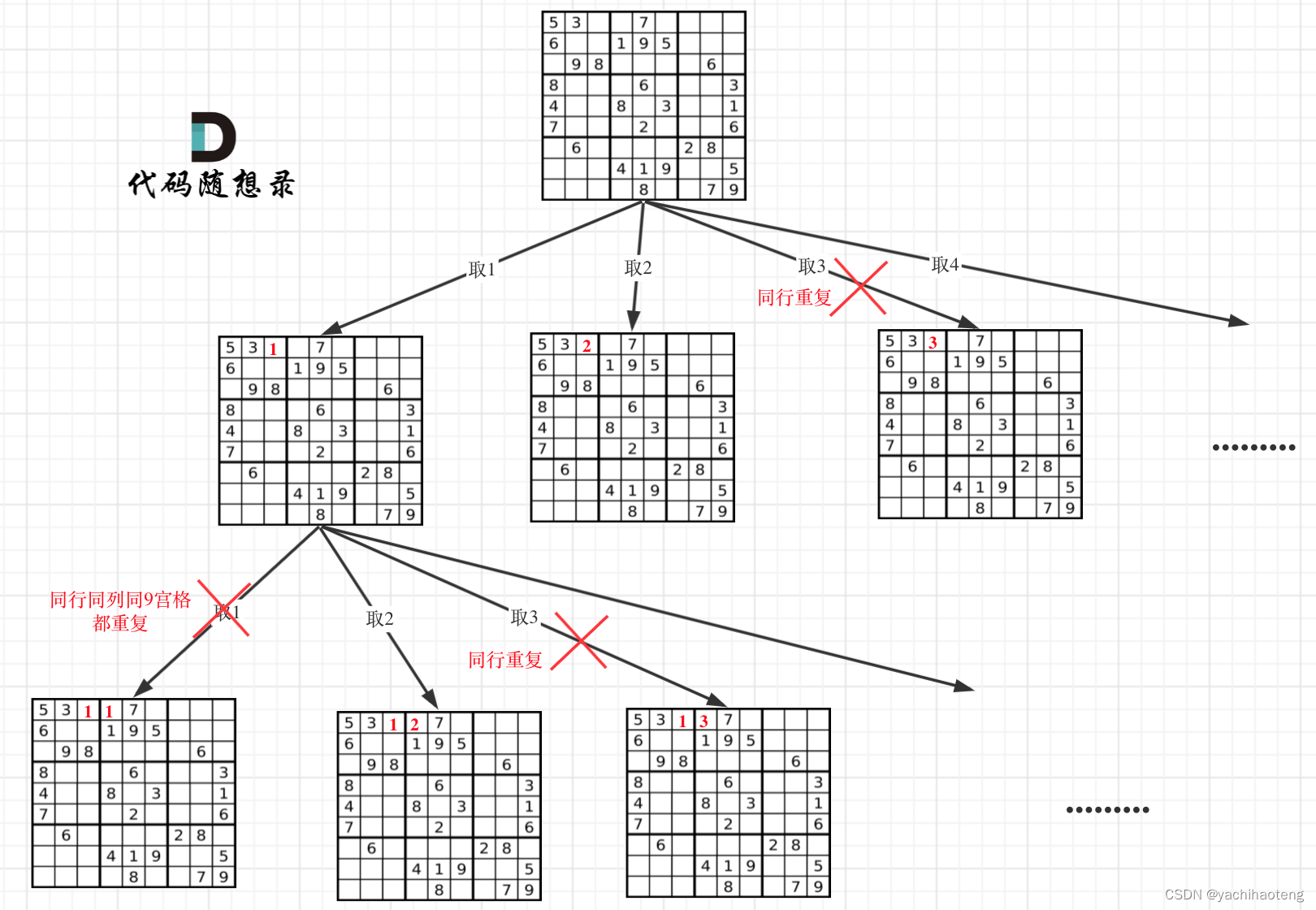
本题中棋盘的每一个位置都要放一个数字(而N皇后是一行只放一个皇后),并检查数字是否合法,解数独的树形结构要比N皇后更宽更深。用部分树来表示为:
注意:本题不需要遍历所有的结果,只需要找到一个结果就可以返回,因此本题的返回值不再是void,而是bool,这样能够在找到一个答案之后立马进行返回。
代码:
class Solution {
public:
//棋盘问题——二维回溯
char arr[9] = {'1','2','3','4','5','6','7','8','9'}; //设置1-9的字符数组方便遍历
//确定返回值和参数列表,本题返回值需要为bool类型,因为,本题不需要遍历所有的结果,只要找到一个结果就返回即可,因此选择bool类型
bool backtracking(vector<vector<char>>& board) {
//确定终止条件,本题需要终止条件,因为本题中间会遍历错误会进行返回,如果遍历到最后也无需判断当前情况。
//确定单层递归逻辑——两层循环
//遍历行
for(int i = 0; i < board.size(); i++) {
//遍历列
for(int j = 0; j < board.size(); j++) {
if(board[i][j] != '.') continue; //找到第一个空格点
//进行插入数字尝试
for(char k : arr) {
//判断当前位置是否可以插入
if(isvalid(board, i, j, k)) { //可以插入的话进入下一层循环
board[i][j] = k;
//当后面的结果回传回来
if(backtracking(board)) return true;
board[i][j] = '.'; //回溯
}
}
//当前位置1-9都不行,说明无法得到答案
return false;
}
}
//完成所有的遍历
return true;
}
//判断函数,参数列表分别为,原数组,行,列,插入的元素
bool isvalid(vector<vector<char>>& board, int row, int col, char val) {
//判断行是否重复
for(int j = 0; j < board.size(); j++) {
if(board[row][j] == val) return false;
}
//判断列是否重复
for(int i = 0; i < board.size(); i++) {
if(board[i][col] == val) return false;
}
//判断九宫格内是否有重复
//确定九宫格位置
int startrow = row / 3 * 3, startcol = col / 3 * 3;
for(int i = startrow; i < startrow + 3; i++) {
for(int j = startcol; j < startcol + 3; j++) {
if(board[i][j] == val) return false;
}
}
return true;
}
void solveSudoku(vector<vector<char>>& board) {
backtracking(board);
}
};回溯总结
文档讲解:代码随想录回溯总结
回溯算法本质是一个暴力搜索的算法,并不是什么高效的算法。
回溯是递归的副产品,只要有递归就会有回溯,所以回溯法也经常和二叉树遍历,深度优先搜索混在一起,因为这两种方式都是用了递归。
回溯算法一般能够解决5类问题:
- 组合问题:N个数里面按一定规则找出k个数的集合
- 排列问题:N个数按一定规则全排列,有几种排列方式
- 切割问题:一个字符串按一定规则有几种切割方式
- 子集问题:一个N个数的集合里有多少符合条件的子集
- 棋盘问题:N皇后,解数独等等
回溯算法的过程,可以抽象为树形结构,因此解题的时候,可以通过画树形结构辅助做题。
回溯算法三部曲模版:
void backtracking(参数) {
if (终止条件) {
存放结果;
return;
}
for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {
处理节点;
backtracking(路径,选择列表); // 递归
回溯,撤销处理结果
}
}