这
* 图的深度遍历过程本身以及所涉及的相关思想记录
⚪第一部分:构建图
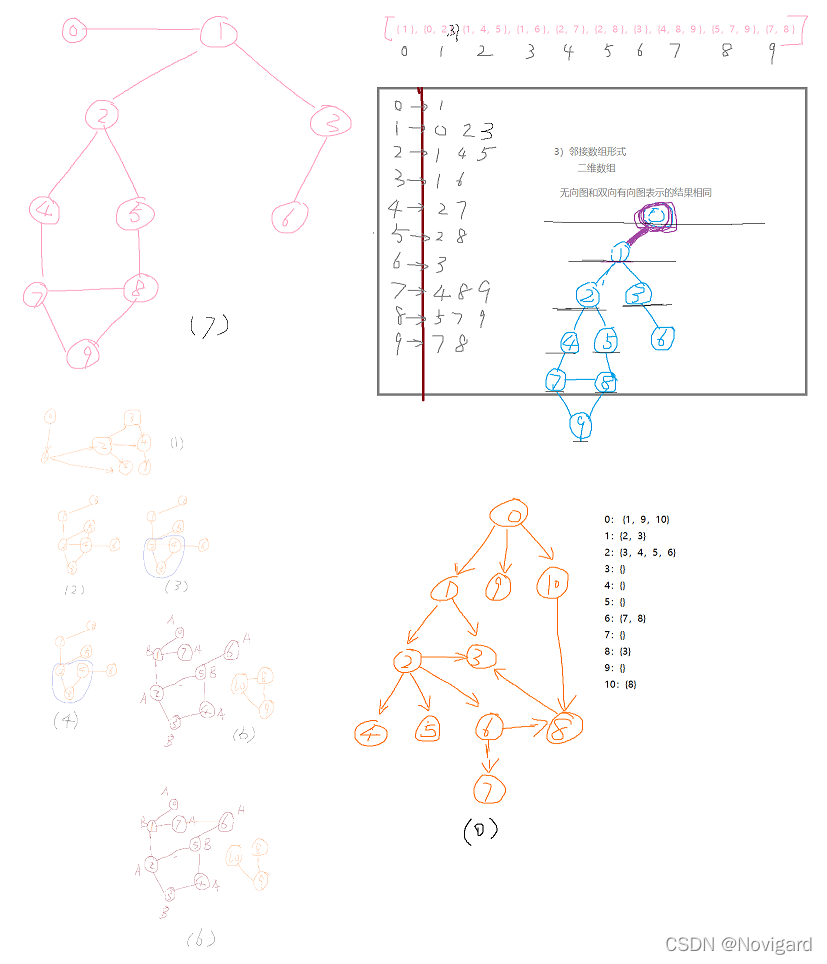
图0、图1为有向图
图2、3、4、5、6、7是无向图
注:图0中含有偶数环,图2、图3、图4、图5、图6、图7中含有奇数环
上述8个图的创建均基于“邻接数组”,即二维数组,leetcode中也常用该方式表示一些图,不过不管使用哪种方式表示图,均可定义为自己所采用的图结构(graphx)
typedef struct Gnode {
int val;
int in;
int out;
vector<struct Gnode*>nexts;
vector<struct Gedge*>edges;
Gnode(){}
Gnode(int val) {
this->val = val;
this->in = 0;
this->out = 0;
}
}Gnodex,*pGnode;
typedef struct Gedge {
int weight;
pGnode from;
pGnode to;
Gedge() {}
Gedge(int weight, pGnode from, pGnode to) {
this->weight = weight;
this->from = from;
this->to = to;
}
}Gedgex,*pGedge;
typedef struct graph {
unordered_map<int, pGnode>node; //用这种方法直接能查到图中是否存在某个值的节点
unordered_set<pGedge>edge;
}graphx,*pgraph;
//有向图实例(1)
vector<vector<int>>vcrty1{ { 1 },{ 2,5 },{ 4,5 },{ 4 },{ 6 },{},{} };
//无向图实例(2)
vector<vector<int>>vcrtw2{ { 1 },{ 0,2 },{ 1,3,4,5 },{ 2,4 },{ 2,3,5,6 },{ 2,4 },{ 4 } };
//无向图实例(3)
vector<vector<int>>vcrtw3{ { 1 },{ 0,2 },{ 1,3,4,5 },{ 2,4 },{ 2,3,6 },{ 2 },{ 4 } };
//无向图实例(4)
vector<vector<int>>vcrtw4{ { 1 },{ 0,2 },{ 1,3,5 },{ 2,4 },{ 3,6 },{ 2 },{ 4 } };
//无向图实例(5)
vector<vector<int>>vcrtw5{ { 1 },{ 2,7 },{ 1,3,5 },{ 2,4 },{ 3,5 },{ 2,6 },{ 5 },{ 1 },{ 9,10 },{ 8,10 },{ 8,9 } };
//无向图实例(6)
vector<vector<int>>vcrtw6{ { 1 },{ 2,7 },{ 1,3,5 },{ 2,4 },{ 3 ,5 },{ 2,4,6 },{ 5,7 },{ 1,6 },{ 9 },{ 8,10 },{ 9 } };
vector<vector<int>>vcrtw7{ {1},{0,2,3},{1,4,5},{1,6},{2,7},{2,8},{3},{4,8,9},{5,7,9},{7,8} };
//(转换模板)
//第一个:数组形式(邻接数组) [[1],[],[]]
//数组形式(邻接数组) [[1],[],[]]
//链表形式(邻接链表)
//三维表形式
//邻接矩阵形式
graphx crtgraph(vector<vector<int>>& graph) {//使用该函数创建图,graphx结构体内部信息很多
int size = graph.size();
graphx gra;
for (int i = 0;i < size;++i) {
pGnode p1 = new Gnode(i);
if (gra.node.find(i) == gra.node.end()) gra.node.insert({i,p1});
for (int j = 0; j < graph[i].size(); ++j) {
pGnode p2 = new Gnode(graph[i][j]);
if(gra.node.find(graph[i][j])==gra.node.end()) gra.node.insert({ graph[i][j],p2 });
gra.node.find(i)->second->nexts.push_back(p2);
gra.node.find(i)->second->out++;
gra.node.find(graph[i][j])->second->in++;
}
}
return gra;
}
graphx g1 = crtgraph(vcrty1);//有向图1
graphx g2 = crtgraph(vcrtw2);//无向图2
graphx g3 = crtgraph(vcrtw3);//无向图3
graphx g4 = crtgraph(vcrtw4);//无向图4
graphx g5 = crtgraph(vcrtw5);//无向图5
graphx g6 = crtgraph(vcrtw6);//无向图6
graphx g7 = crtgraph(vcrtw7);//无向图7
⚪ 第二部分:给出DFS遍历的递归过程和类似思想的应用、解释。
(LC802找到最终安全状态:有向图的环问题)
/*
1.递归版本(self),利用flag和tag数组处理路径,并利用cache记录当前路径
返回安全的节点(leetcode),与环相关的节点,包括上游节点都不安全,
只有完全没有涉及到环的节点才算作安全。受到“感染”的节点均为不安全节点。
*/
首先,有两个概念:
//1.访问过和没访问过
//2.安全和不安全
//访问过不一定安全,访问没访问用visited(或tag)数组表示;一个节点安不安全要看它所有下游出度的安全状态,如果所有出度都安全,当前节点安全,否则不安全。
bool dfs(vector<vector<int>>& graph, //原图使用邻接数组表示
vector<bool>& flag, //安全节点记录数组
vector<int>& cache, //路径跟踪数组
int m, //当前所遍历节点
vector<bool>& tag) //遍历标记
{
//没有环存在,用true表示
if (tag[m] == false) {
int gc = 0;
for (int i = 0; i < graph[m].size(); ++i) {
if (tag[graph[m][i]] == true && flag[graph[m][i]] == false) {//访问过,不安全
for (int j = 0; j < cache.size(); ++j) {
if (flag[cache[j]] == true)flag[cache[j]] = false;
}
continue;
}
else if (tag[graph[m][i]] == true && flag[graph[m][i]] == true) { //访问过,安全
continue;
}
//这一段检查是否有重复,有的话路径上所有节点加入黑名单
for (int v = 0; v < cache.size(); ++v) {
if (graph[m][i] == cache[v]) {
gc = 1;
for (int j = 0; j < cache.size(); ++j) {
if (flag[cache[j]] == true)flag[cache[j]] = false;
}
break;
}
}
//没有重复,在该路径上增加当前节点
if (gc == 0) {
cache.push_back(graph[m][i]);
if (tag[cache.back()] == false) { //如果所有出度没有访问完,(此时无法判断安全与否),所以继续访问尾巴节点(递归)
dfs(graph, flag, cache, cache.back(), tag);
}
}
}
tag[m] = true;//所有出度访问完成才算true啊
cache.pop_back();
}
return false;
}
//下面再写一个遍历所有图节点的总循环函数即可,防止出现非连通图的情况,最后返回所有安全的节点。这里不再赘述由上面代码可知,安全节点记录数组flag中对于整个图中每一个节点都给予了安全性标记,这种方式比较全,tag数组(也可以叫做visited数组)对于图中每一个节点都给予了访问标记。即:整体循环体是基于一个节点的所有出度进行的,并在该循环体中对递归子层(子函数)所遇到的节点的安全性和访问性进行判断,类似的,如果问题中需要的是别的性质,这里的安全性可以更换为别的性质,并通过引用容器的方式达到每层使用的目的。在本问题中,如果是访问过且不安全,那么上面记录的所有路径中节点都不安全(由于这种方式没有使用递归函数的返回值,所以不可避免地需要增加一个flag安全性标记数组,如果是用dfs函数返回值表示当前m节点是否安全,则无需加入flag数组,但那就必须要等到所有递归层函数执行完才能知道上层节点是否安全。但使用函数返回值的方式代码简洁,逻辑更为清晰。故各有利弊。);第二个for循环是判断当前所遇到的节点是否在路径中出现过,如果出现,离重复节点相差几个(奇数环还是偶数环可通过这个方式判断)该方式稍微增加一点东西就可以搞定图的二分问题,这种底层的完全记录剖析型重代码对原理的理解有一定好处,前期需要多记忆,练习,后期熟练后变可化为内功;最后一段在判断当前节点安全后,将把第一个邻居节点(子层节点)放入路径中,递归该节点,递归函数返回当前层后把这个节点弹出(该节点所有出度遍历完成),通过该方式可以详细回溯记录每一条路径。(即遍历完A节点的所有子节点后A节点出栈,这时应该返回上一层for里面,找A的兄弟节点B继续递归,B经历多层递归后返回到本体并弹出自己,再找其他同层兄弟进行遍历,直到该层所有遍历完成。这个栈,即cache,就是路径记录的含义。
/*
重要信息:
1.必须知道一个节点的所有邻居节点,
2.整体过程是从前往后访问该层“子节点”的所有邻居节点
3.(但如果第一个“子节点”有自己的子层节点,则先递归,
4.等递归层返回后再访问原来层的后续节点,如果该层所有“子节点”访问完毕,visited数组在该节点做出标记(如visited[m]=2)(针对有向图,无向图会出现邻居回访的情况)
对于无向图来说,如果某个递归层函数拿到的节点是已经访问过的,在单次访问(如单次深度遍历)过程中,该节点只有两个状态(访问过、未访问过),如果该节点访问过了,标记肯定会变,此时可以直接结束当前的“小递归函数”,并返回值给上一层的“大递归函数”,上一层的“大递归函数”会继续通过循环体创建下一个小递归函数,如果这次的“小递归函数”可以继续递归,那自己会创建“更小的递归函数”进行执行。系统栈中的所有递归函数都在等待下一层的返回(无论是返回非空值还是返回空值)。某层的递归函数在得到子层递归结果后执行后续步骤。
一旦触发了可递归条件,“大递归函数”会创建“小递归函数”,以此类推,上层函数的目的是得到下层函数的结果或为下层函数执行创造条件(该情况为可能是引用参数的变化,即无返回值递归函数)
在图(类似多叉树)深度遍历过程中,无论有向图、无向图,当前节点的直接邻居个数(即子层节点个数)与小递归函数个数相同。
比方说,图中有37个节点,那么需要创建37个递归函数(线程)来搞定DFS过程。复杂度O(N)。
在迷宫matrix图中,上下左右、左前右后左后右前 共八个方向,如果需要递归寻找其他路径中的成果(返回值什么的),相当于
遍历一颗八叉树。写八个dfs子层函数即可,只不过参数需要琢磨一下。
这里要说明一下,二叉树的遍历之所以不需要通过循环体,是因为递归子层函数所需要的参数无非就是二叉树左右节点,每层都是这样。
所以相当于已知递归层的参数(2个),以此给出即可,复杂度同样为O(N)。
*/
*下面给出带返回值的方法:
bool dfs(
vector<vector<int>>& graph, //邻接数组
int m,//当前节点
vector<int>& visited//访问标记数组
) {
//do sth... 这里可以是给出当前节点的值输出,cout、printf、push_back进路径数组等DFS操作
visited[m] = 1;//每个节点处理时都会有一个线程(递归层函数),所以进来之后状态直接变为访问过,至于有没有访问完,需要等下面循环中所有的递归层都返回给当前层后,即可知道。
for (int neighbor : graph[m]) {
if (visited[neighbor] == 0) {//一次都没访问过的子层节点,拥有自己独立深搜的机会
if (!dfs(neighbor, graph, visited)) {
return false;
}
}
else if (visited[neighbor] == 1) {//访问过但没访问完的节点重新被遇到,而且是有向图
//所以不可能是才遇到的立即回头(无向图)情况
return false; //中了这个else if的节点绝对是环节点。(精髓)
}
}
visited[m] = 2;//所有节点访问完,中途未返回false,一直坚持到现在的必须是安全的(无环)
return true; //正是基于此,上一步如果遇到visited值为2的也不会返回假。
}*通过这种带bool返回值的dfs可以通过巧妙利用有向图的特性(不会出现无向图中连续节点互相回访的情况,故visited[m]等于1不会对m下层的节点造成影响,不需要增加cache缓存记录当前路径,因为底层节点再遇到visited[m]==1的情况一定是环),不过该方式要求底层所有递归函数执行完之后才能获得上层的布尔值。
⚪ 下面给出二分图(奇数环和偶数环的判定)(无向图,有向图通用)
和第一种方法类似,增加了路径记录数组cache,但是不同的是,无需增加安全判定数组flag,只需要在遇到环的时候判断cache[v]和cache最大下标的差距即可,同时增加相邻节点回访的排除语句:(cache.size()>=2&&cache[cache.size()-2]== graph[m][i] 因为当前路径如果有环,那么必须至少存在三个节点,无向图来回虽然可以无限循环访问,但那不叫环,所以手动排除那种情况后即可正确运行。
bool dfs_at(
vector<vector<int>>& graph,
vector<int>& cache,
int m,
vector<bool>& tag)
{//没有环存在,用true表示
if (tag[m] == false) //没有遍历完,遍历当前(值为m的)节点
{
for (int i = 0; i < graph[m].size(); ++i) //check all nexts of current node,检查当前节点的所有相邻节点
{
int gc = 0;
if (tag[graph[m][i]] == true||(cache.size()>=2&&cache[cache.size()-2]== graph[m][i])) //访问过
{
continue;
}
//这一段检查是否有重复,有的话路径上所有节点加入黑名单
for (int v = 0; v < cache.size(); ++v)
{
//cout << "dangqian=" << graph[m][i] << " " << endl;
if (graph[m][i] == cache[v])
{
gc = 1;
//cout << "core==" << cache.size() - v << endl;
if ((cache.size() - v)%2!=0) //如果环中节点个数为奇数,无法二分,此时返回false
{
return false;
}
break;
}
}
//没有重复,在该路径上增加当前节点并继续往深处搜索
if (gc == 0)
{
cache.push_back(graph[m][i]);
//for (auto i : cache)cout << i << " "; cout << endl;
if (tag[cache.back()] == false) //如果仍有出度没访问完,继续访问尾巴节点(递归)
{
if ( (!dfs_at(graph, cache, cache.back(), tag)) )
{
return false;
}
}
}
}
tag[m] = true;//所有出度访问完成才算true啊
cache.pop_back();
}
return true;
}末尾的cache.pop_back()作为完全被访问过节点的弹出操作存在。
⚪下面给出DFS整体过程的思考,精简化流程、逻辑。
很明显,控制了递归条件后,能进入递归层的节点100%是没有被访问过的,DFS只在第一次访问的时候做出打印操作,随机将该节点访问标记(也可以理解为节点自带属性)置为1,表示访问过;接下来在当前节点的所有出度(nexts)中“依次递归”,每个小递归函数都是一个独立的线程。总共就两个逻辑:1.没访问过的利用循环体中的递归函数按照深度直接访问;2.访问过的直接跳过。整体流程简单清晰。
void dfsBMW(graphx gra,int m,int*&p) {m是节点下标,也是节点值
//do sth..
//printf("%d ", m);//打印操作
//cache.push_back(m); //记录路径操作
//for (auto i : cache)cout << i << " "; cout << endl;//打印路径操作
p[m] = 1;
for (int i = 0; i < gra.node.find(m)->second->nexts.size(); ++i) {
// look current level small guy
if (p[gra.node.find(m)->second->nexts[i]->val] == 0) {
dfsBMW(gra, gra.node.find(m)->second->nexts[i]->val,p);
}
}
}类似的递归思想可以应用至很多问题,程序是灵活的,不断思考,不断进步。