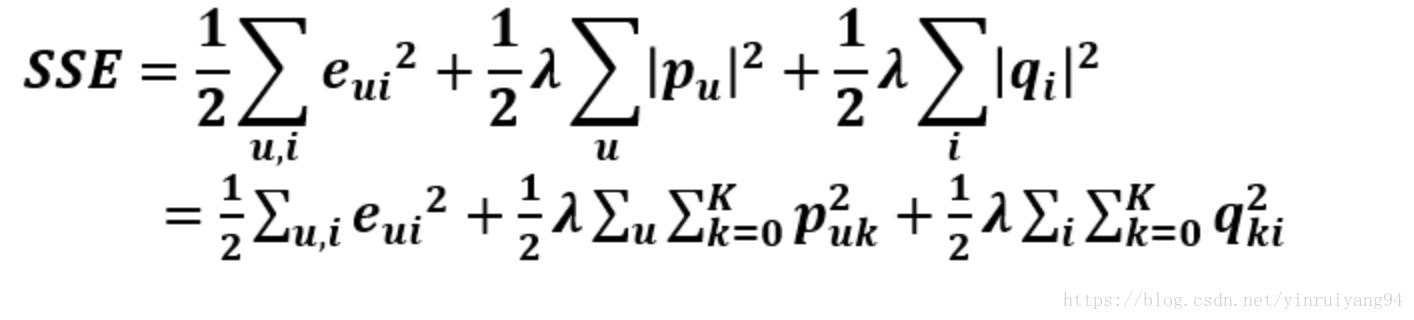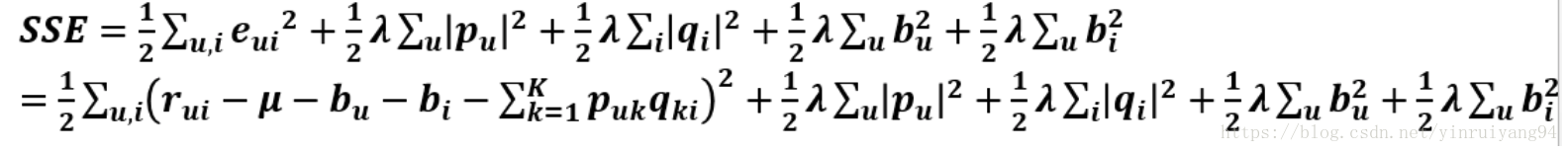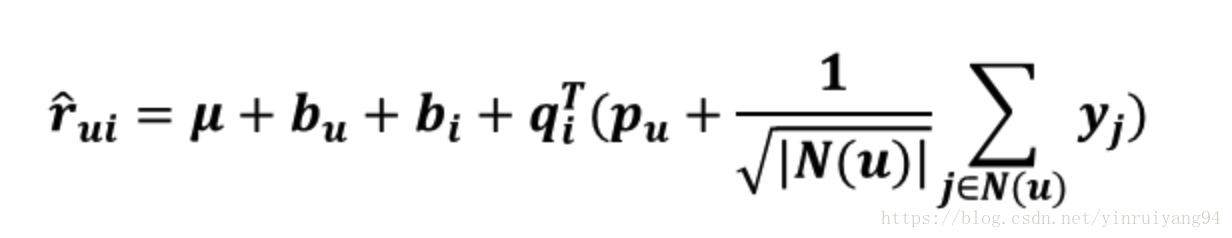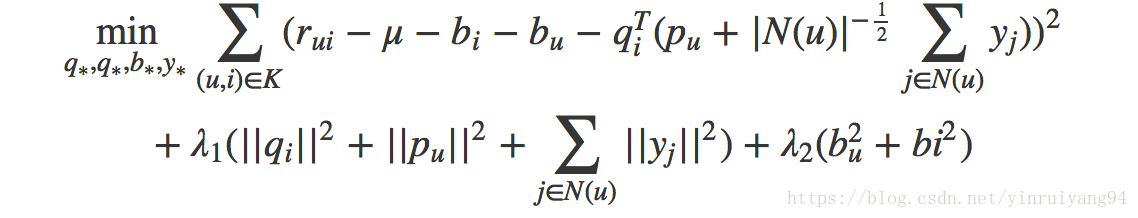[Recommendation System] 推荐系统之协同过滤(CF)算法详解和实现
【推荐系统】协同过滤(CF)算法详解,item-base,user-based,SVD,SVD++
【推荐系统】特征值分解(谱分解)和奇异值分解(SVD),即在PCA上的应用
推荐系统的作用:
- 帮助用户找到想要的商品(新闻/音乐/……),发掘长尾
- 降低信息过载:互联网时代信息量已然处于爆炸状态,若是将所有内容都放在网站首页上用户是无从阅读的,信息的利用率将会十分低下。因此我们需要推荐系统来帮助用户过滤掉低价值的信息。
- 提高站点的点击率/转化率
- 加深对用户的了解,为用户提供定制化服务
推荐算法大致可以分为以下几类:
- 基于流行度的算法
- 协同过滤算法
- 基于内容的算法
- 基于模型的算法
- 混合算法
基于流行度推荐:
就像微博热搜。
优点:计算简单方便。没有冷启动问题,适用于新注册的用户。
缺点:不是个性化推荐。
改进:可以对用户聚类再进行热搜推荐,例如热衷于体育的用户推体育相关的热搜。
协同过滤算法:
见最后。
优点:
基于user和基于item各有千秋。
对于在线网站来说,用户的数量往往大大超过物品的数量,同时物品的数据相对稳定,因此计算物品的相似度不但计算量较小,同时也不必频繁更新。
但是对于视频、新闻网站,item更新迅速,item数据远远超过user,则基于user的更加合适。
基于user的推荐更倾向于推荐热门物品。(因为它推荐的都是别人看过的)
基于item的推荐更倾向于推荐单一种类的物品,缺少多样化。
缺点:
基于user的推荐基于一个有共同喜好的好友的假设,如果一个user没有共同喜好的好友,则user-based效果不好。
基于item的推荐基于一个人喜欢同一种类item的假设,然而一个人要是兴趣广泛,什么都看,则item-based效果不好。
基于内容的推荐:
把用户喜好的关键字和item的关键字作为属性并且作为向量,计算两个向量之间的距离。从而得到user与item之间的相似度。
关键字也有主次之分,可以引入词权的概念,在大量的语料库中通过计算(比如典型的TF-IDF算法),我们可以算出新闻中每一个关键词的权重,在计算相似度时引入这个权重的影响,就可以达到更精确的效果。
优点:基于内容的推荐算法能够很好地解决冷启动问题,并且也不会囿于热度的限制,因为它是直接基于内容匹配的,而与浏览记录无关。
缺点:这种方法会一直推荐给用户内容密切关联的item,而失去了推荐内容的多样性。
基于模型推荐:
可以使用逻辑回归进行预测。
user包含各种属性,一个包含各种属性的user会对一个item产生0到1之间的兴趣。使用逻辑回归进行监督学习。
模型的输出近似1的则为需要推荐的item。
但是不是所有的user属性都对模型有正面影响,所以需要不断地实验和经验来进行属性的组合,从而拟合出最好的模型。
优点:基于模型的算法由于快速、准确,适用于实时性比较高的业务如新闻、广告等。
缺点:而若是需要这种算法达到更好的效果,则需要人工干预反复的进行属性的组合和筛选,也就是常说的Feature Engineering。而由于新闻的时效性,系统也需要反复更新线上的数学模型,以适应变化。
混合算法:
现实情况中,不可能只用一种方式进行推荐,都是多种算法的组合。
我们可以通过给不同算法的结果加权重来综合结果,或者是在不同的计算环节中运用不同的算法来混合,达到更贴合自己业务的目的。
推荐结果评估
当推荐算法完成后,怎样来评估这个算法的效果?CTR(点击率)、CVR(转化率)、停留时间等都是很直观的数据。在完成算法后,可以通过线下计算算法的RMSE(均方根误差)或者线上进行ABTest来对比效果。
通过其他公司其他平台获取我的新用户的信息可以解决冷启动问题。
协同过滤
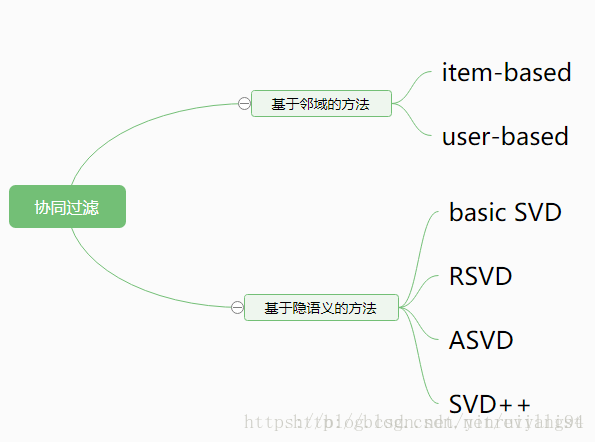
CF算法是推荐算法的一个大分支,基本思想是推荐相似的物品,或者推荐相似用户(隐式或者显式)评分过的物品。
首先,要实现协同过滤,需要一下几个步骤
- 收集用户偏好
- 找到相似的用户或物品
- 计算推荐
要从用户的行为和偏好中发现规律,并基于此给予推荐,如何收集用户的偏好信息成为系统推荐效果最基础的决定因素。用户有很多方式向系统提供自己的偏好信息,而且不同的应用也可能大不相同,下面举例进行介绍:
收集了用户行为数据,我们还需要对数据进行一定的预处理,其中最核心的工作就是:减噪和归一化。
减噪:用户行为数据是用户在使用应用过程中产生的,它可能存在大量的噪音和用户的误操作,我们可以通过经典的数据挖掘算法过滤掉行为数据中的噪音,这样可以是我们的分析更加精确。
归一化:如前面讲到的,在计算用户对物品的喜好程度时,可能需要对不同的行为数据进行加权。但可以想象,不同行为的数据取值可能相差很大,比如,用户的查看数据必然比购买数据大的多,如何将各个行为的数据统一在一个相同的取值范围中,从而使得加权求和得到的总体喜好更加精确,就需要我们进行归一化处理。最简单的归一化处理,就是将各类数据除以此类中的最大值,以保证归一化后的数据取值在 [0,1] 范围中。
以上是获取数据并进行数据清洗的操作,从而得到user-item矩阵。
一维是用户列表,另一维是物品列表,值是用户对物品的偏好,一般是 [0,1] 或者 [-1, 1] 的浮点数值。
就像是这样的:
接下来不论是基于user或item的协同过滤,还是矩阵分解等操作,都是基于这个矩阵的操作。
对于user-based和item-based两种,我们需要进行的是向量的相似度计算。
关于相似度的计算,现有的几种基本方法都是基于向量(Vector)的,其实也就是计算两个向量的距离,距离越近相似度越大。
几种度量:
接下来就是根据上述得到的矩阵和度量方式来计算推荐。
两种方式就不多说了。
以上是直观的使用矩阵中的数据进行的推荐。
接下来是使用矩阵中的隐语义进行的推荐:
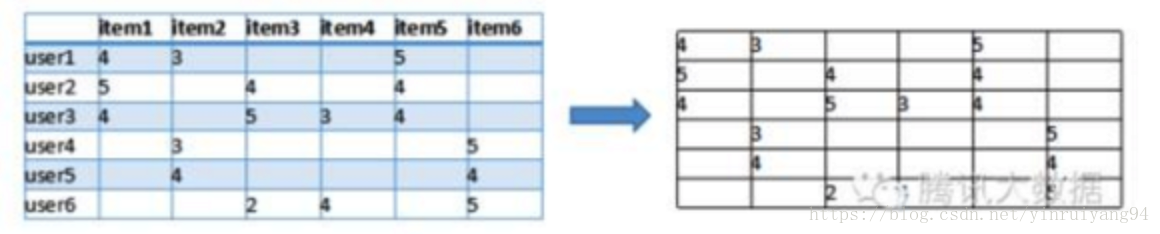
我们认为这个矩阵中的数字不仅仅包含了简单的喜好程度,而是有更深层的语义在其中。
例如,可以把user表示成一个n维向量,每一维代表一个特征,例如对颜色的偏好 、对重量的要求 、设计风格的偏好 、价格偏好 …
相应的item,也可以表示成n维:颜色、重量、风格、价格…
然后通过两个特征向量的内积来判断用户对一个物品的喜好程度。在具体的模型中,向量每个维度的意义并不能人为给定,模型会自己通过最小化损失来学习这两个向量。虽然这个方法不要求共同评分,但推荐系统还是面临很大的数据稀疏问题。
- Basic SVD和RSVD
- SVD++
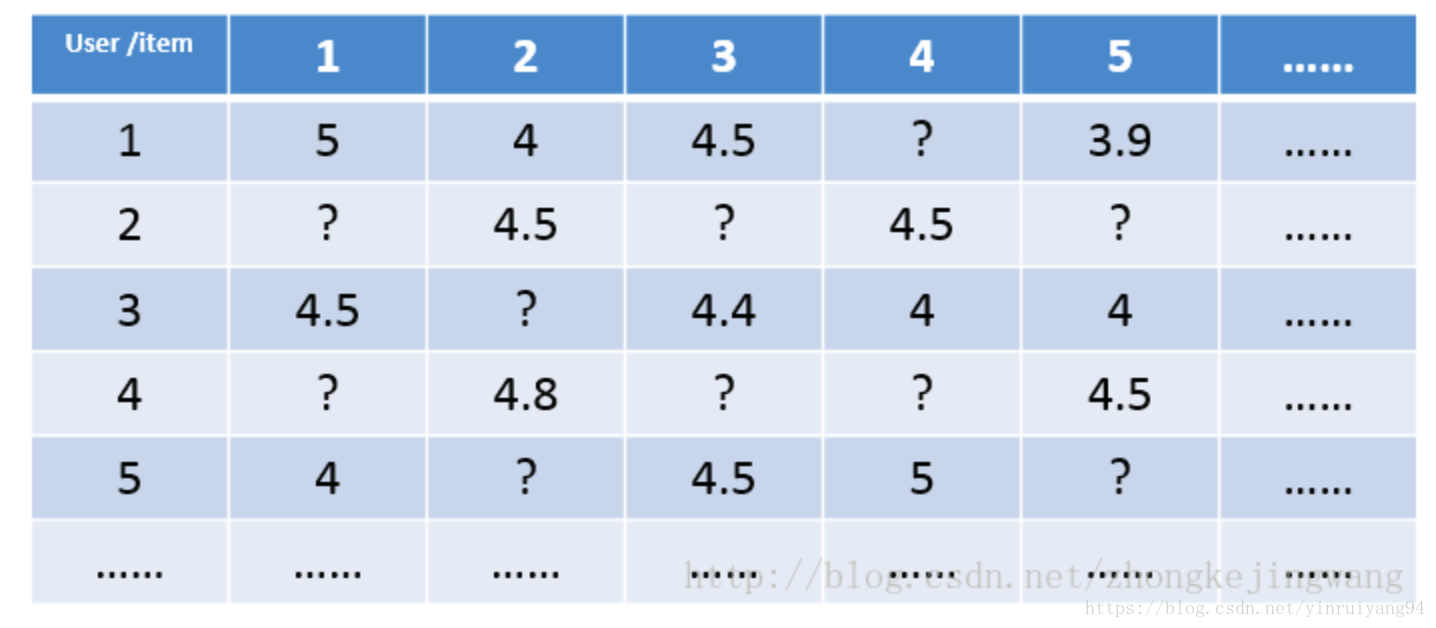
这是一个极其稀疏的矩阵,这里把这个评分矩阵记为R,其中的元素表示user对item的打分,“?”表示未知的,也就是要你去预测的,现在问题来了:如何去预测未知的评分值呢?SVD可以证明对任意一个矩阵A,都有它的满秩分解:
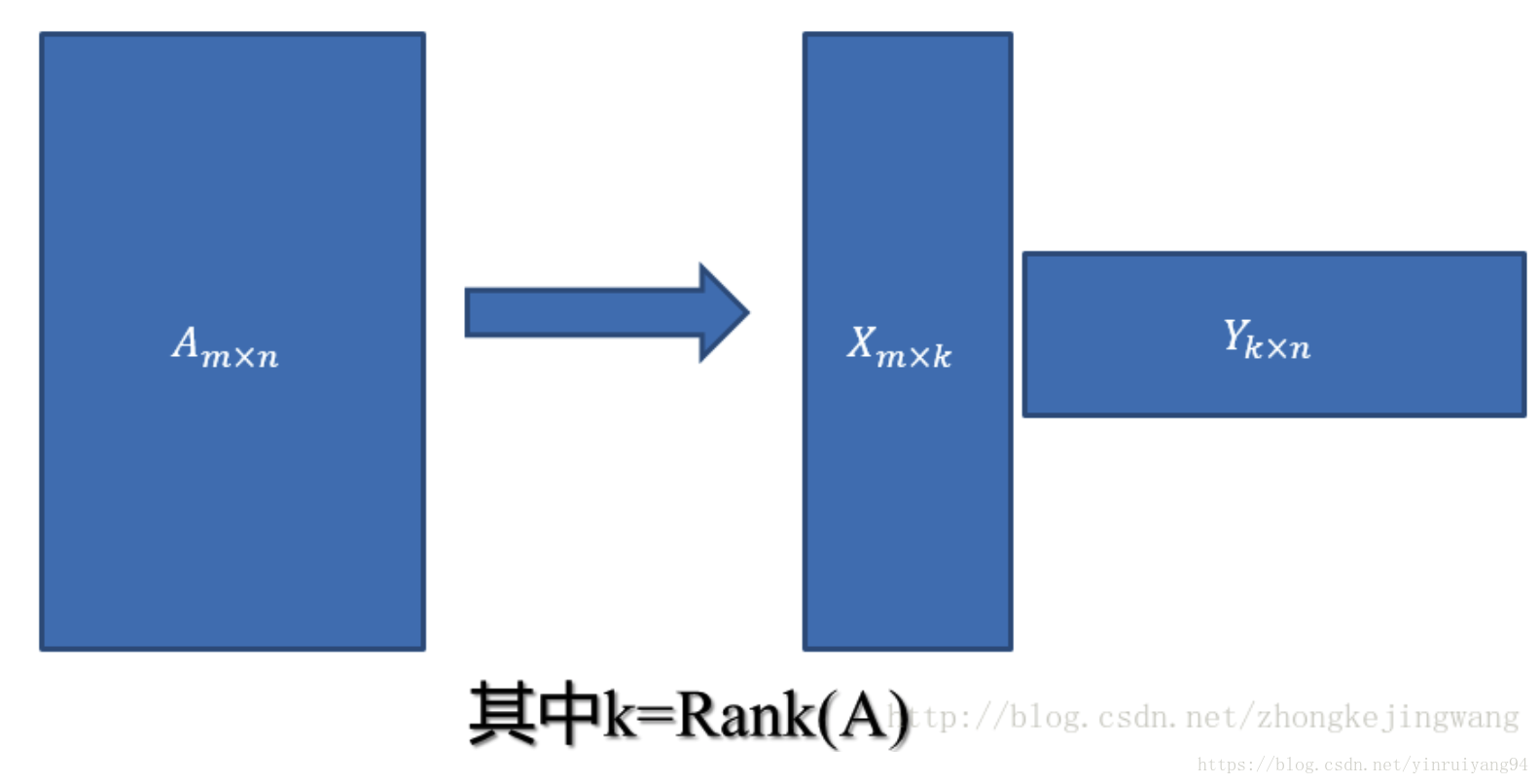
所以上边的评分矩阵R也存在这样一个分解,所以可以用两个矩阵P和Q的乘积来表示评分矩阵R:
RUxI = PUxKQKxI
则:
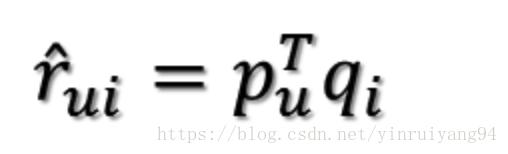
是某一个user对某一个item的评分。

以上误差加上正则项得到最终的SVD目标函数:
用户对商品的打分不仅取决于用户和商品间的某种关系,还取决于用户和商品独有的性质,我们希望将这些性质用基线评分(baseline estimates)来表示。
例如,我们希望得到小明对电影《泰坦尼克号》的评分,首先我们得到所有电影的评分均值μ为3.7分。然后,我们得知该电影非常好看,评分可能比平均分高0.5.另外,小明是一个非常苛刻的观众,评分可能比平均分低0.3.我们得到小明对电影《泰坦尼克号》的基线评分3.7+0.5-0.3=3.9分。
定义用户u对物品i的评分rui的基线评分bui:
bui=μ+bu+bi
得到:
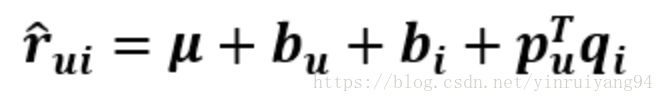
这就是RSVD:
在茫茫item中,用户打分过的item可谓是少之又少,而用户浏览过、仔细看过等动作也可以看做是一种偏好。例如在电影推荐中,某部电影user看过但没评分,我们也可以认为这个user偏好于这种特征的电影。因此在SVD中引入这种隐式反馈。
我们可以在user向量中加入这种隐式反馈来表示user的这种隐式的特征。
N(u)
用户u行为记录(包括浏览的和评过分的商品集合),是收缩因子取集合大小的根号是一个经验公式,并没有理论依据。
目标函数为:
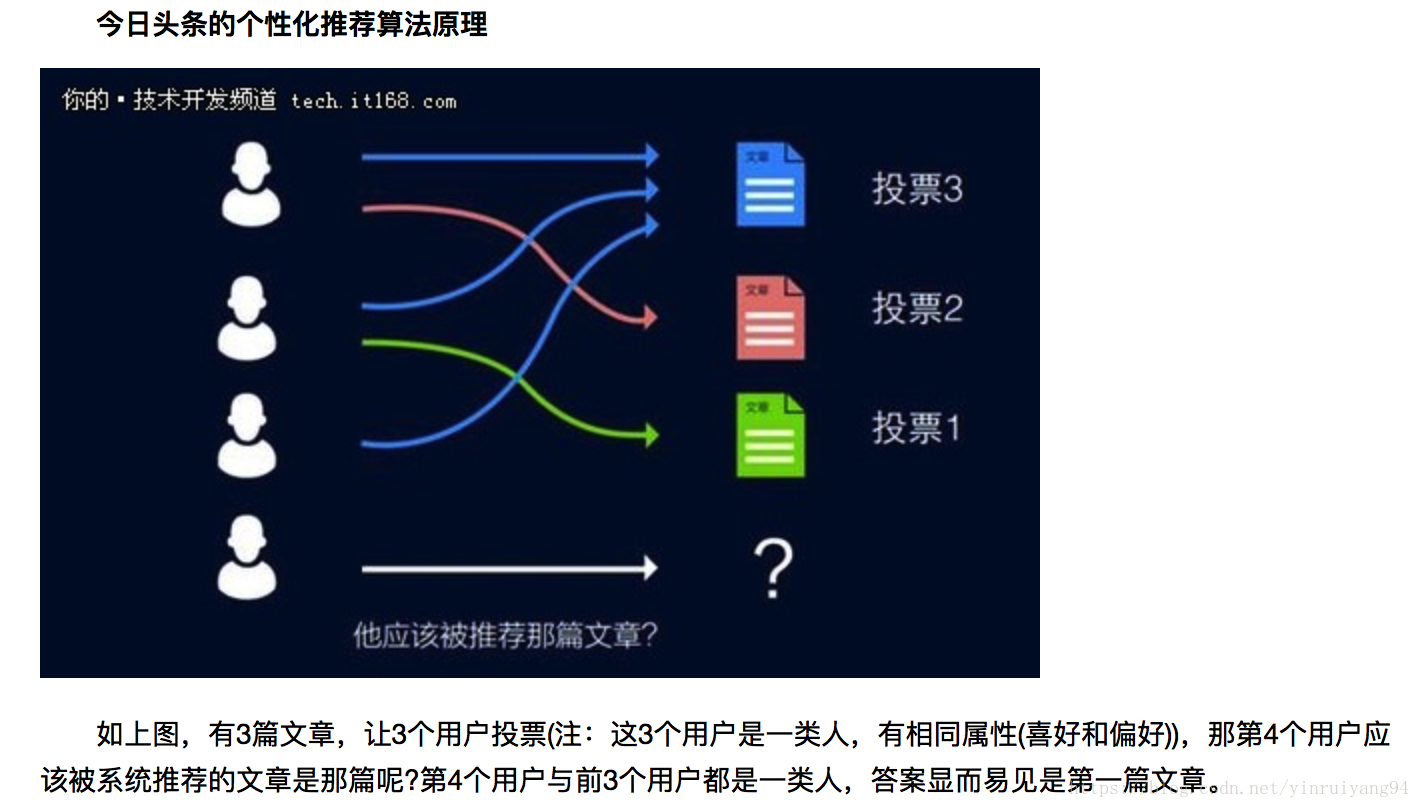
今日头条推荐算法简述:
没错,今日头条的个性化推荐算法原理就是基于投票的方法,其核心理念就是投票,每个用户一票,喜欢哪一篇文章就把票投给这篇文章,经过统计,最后得到结果很可能是在这个人群下最好的文章,并把这篇文章推荐给同人群用户过程就是个性化推荐,实际上个性化推荐并不是机器给用户推荐,而是用户之间在互相推荐,看起来似乎很简单,但实际上这需要基于海量的用户行为数据挖掘与分析。
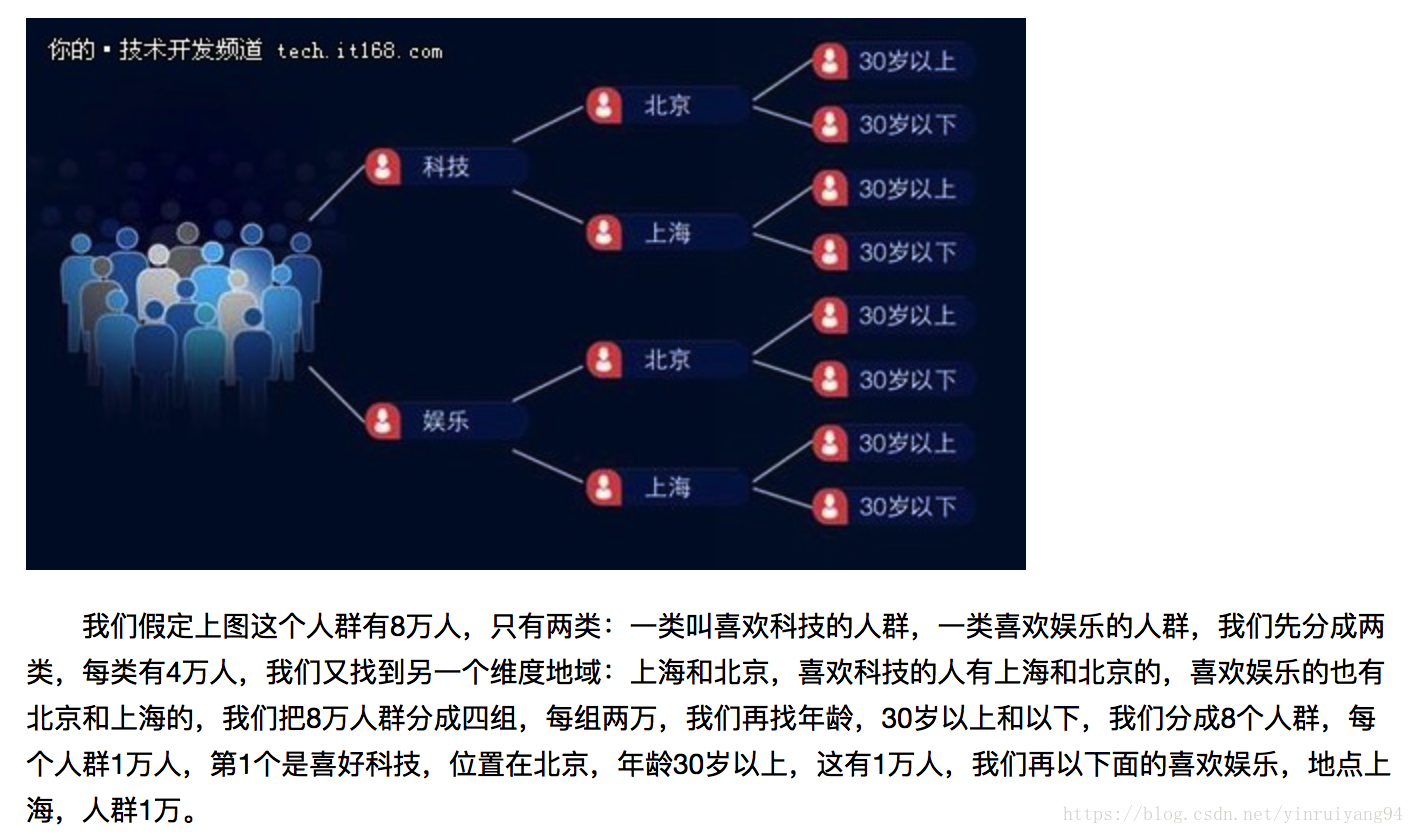
首先,要划分人群:
太大的人群就失去了个性化推荐的意义,太小的人群的投票结果无法做到精细的推荐。
按不同的维度进行划分,如下:
判断一个人属于怎样的人群相对简单。比如地域,用户的手机在什么区域,就可以认为用户是什么地域的;比如说用户兴趣,可以根据用户的阅读习惯去判断,用户会经常去看科技的文章,那就可以判断用户属于科技的人群;再比如说用户的好友关系,用户在今日头条上面注册了,用户的好友都是娱乐圈的人,则该用户很有可能也是娱乐圈的人;所以通过用户在今日头条上行为,以及用户客观的地理位置信息,就能判断用户到底属于一个什么样的人群。
可以认为今日头条的推荐就是将用户聚类,让用户之间互相推荐。至于具体的推荐算法,肯定会想开头的参考文章中说的这么简单了。