1. 题目来源

链接：2844. 生成特殊数字的最少操作

2. 题目解析

模拟题目，看着很简单，但是如何把代码写对、写的效率高，还是需要些技巧的。

思路：

• 分类讨论：
  • 00 这种情况肯定不会出现，因为不包含前导0。至少也是个 xx00。
  • 00、25、50、75 这四种情况属于两位能被 25 整除的。
  • 0 属于一位能被 25 整除的。
  • 全部删除，属于没有找到合法条件的全部删除。
• 单独一个 0 不是很好处理，可以优先特判去处理。
• 剩余的 00、25、50、75 这类，可以倒序遍历，采用两次遍历的方式：
  • 如果第一个是 0，那么需要再找到前面的 0 或者 5。此时针对下标 0 已经是一个最优情况了。
  • 如果第一个是 5，同理向前找 2、7 即可。
• 最终统计下结果即可。
• 上述方法为两次遍历。会对 num 遍历多遍。

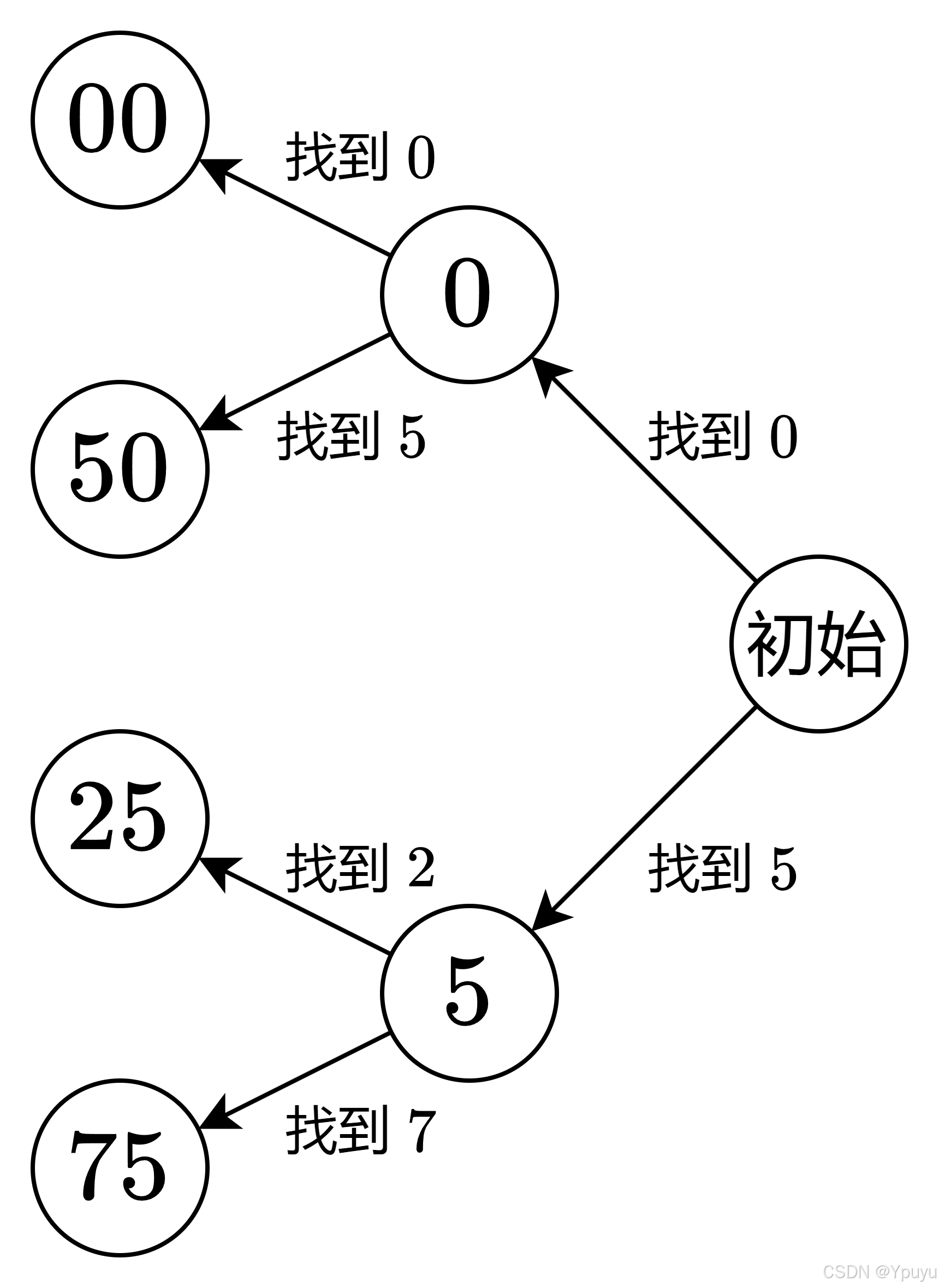
关于 1次遍历的方式，也是我一开始最先想的方式，参考灵神题解绘图：

根据该图，在从右往左遍历的过程中：

• 在之前找到 0 的情况下，如果当前数字 num[i] 是 0 或者 5，则立刻返回 n−i−2。
• 在之前找到 5 的情况下，如果当前数字 num[i] 是 2 或者 7，则立刻返回 n−i−2。
• 否则，如果 num[i] 是 0，标记我们找到了 0。
• 否则，如果 num[i] 是 5，标记我们找到了 5。
• 如果循环中没有返回，则最后返回 n 或者 n−1，取决于我们是否找到了 0。

• 时间复杂度：$O(n)$
• 空间复杂度：$O(1)$

两次遍历：

class Solution {
public:
    int minimumOperations(string num) {
        int n = num.size();
        
        int res = n;
        for (int i = 0; i < n; i ++ ) {
            if (num[i] == '0') {
                res = n - 1;
                break;
            }
        }
        
        bool has_5 = false, has_0 = false;
        for (int i = n - 1; ~i; i -- ) {
            int t = n;
            if (has_5 == false && i > 0 && num[i] == '5') {
                for (int j = i - 1; ~j; j -- ) {
                    if (num[j] == '2' || num[j] == '7') {
                        t = n - j - 1 - 1;
                        has_5 = true;
                        break;
                    }
                }
            }

            if (has_0 == false && i > 0 && num[i] == '0') {
                for (int j = i - 1; ~j; j -- ) {
                    if (num[j] == '0' || num[j] == '5') {
                        t = n - j - 1 - 1;
                        break;
                    }
                }
            }

            res = min(res, t);
            if (has_0 && has_5) return res;
        }

        return res;
    }
};

一次遍历：

class Solution {
public:
    int minimumOperations(string num) {
        int n = num.size();
        bool f_0 = false, f_5 = false;
        for (int i = n - 1; i >= 0; i -- ) {
            char c = num[i];
            if (f_0 && (c == '0' || c == '5') || 
               (f_5 && (c == '2' || c == '7'))) {
                return n - i - 2;
               }

            if (c == '0') f_0 = true;
            else if (c == '5') f_5 = true;
        }

        return n - f_0;
    }
};