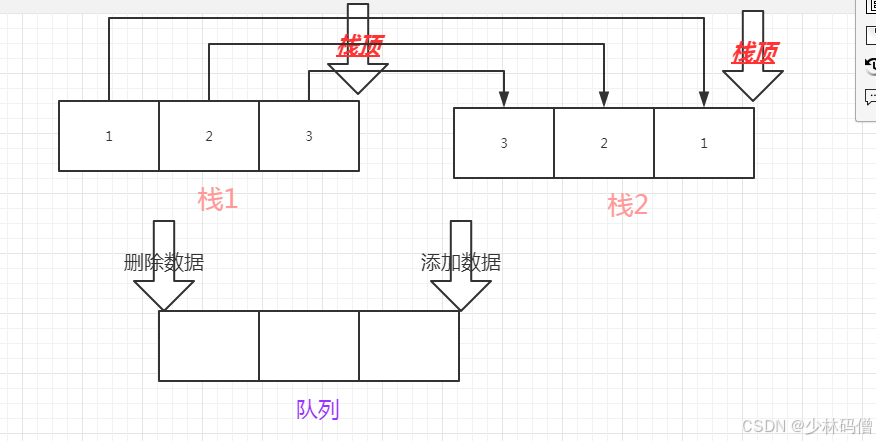
队列
队列是一种特殊的线性表,特殊之处在于它只允许在表的前端(front)进行删除操作,而在表的后端(rear)进行插入操作,和栈一样,队列是一种操作受限制的线性表。进行插入操作的端称为队尾,进行删除操作的端称为队头。
对列的添加 insert append
队列的取值 列表[-1] 列表[0]
队列的删除 pop() pop(0)
栈
栈(stack)又名堆栈,它是一种运算受限的线性表。其限制是仅允许在表的一端进行插入和删除运算。这一端被称为栈顶,相对地,把另一端称为栈底。向一个栈插入新元素又称作进栈、入栈或压栈,它是把新元素放到栈顶元素的上面,使之成为新的栈顶元素;从一个栈删除元素又称作出栈或退栈,它是把栈顶元素删除掉,使其相邻的元素成为新的栈顶元素。
只允许在栈的栈顶来操作。
添加元素用append(push),称作是进栈,入栈或者压栈
取值列表[-1],因为它只能从栈顶来取值,相当于取列表的最后一个值,所以用索引-1.
删除元素pop()从后端开始删除。称作是出栈或者退栈。
1. 两个栈实现一个队列:[^本题考点 队列 栈]
用两个栈来实现一个队列,完成队列的Push和Pop操作。 队列中的元素为int类型。
……解析:
定义一个类,首先这个类要具备两个属性,一个是压栈,一个是出栈。
因为要两个栈来实现一个队列:进行插入操作的端称为队尾,进行删除操作的端称为队头。
那么如何用:两个栈实现一个队列?
栈: 先进后出
队列:先进先出
如图所示:
队列从一头添加数据,从一头删除数据。
所以我们需要让两个栈
一个栈实现添加数据
即:self.acceptStack=[] 它拥有一个push的方法,用来作为队列的一端的添加数据 功能 用append来实现
self.acceptStack.append(node)
另一个栈实现删除数据:
即:self.outputStack = [] 它拥有pop 的方法,用来作为队列的另一端的删除数据的功能 用pop 来实现
但是我们要实现的是队列的先进先出,也就意味着 如果说我们添加数据的栈中添加了一个数据,那么我们另一个删除数据的栈中,也要相应的删除这个数据,所以说这两个栈中的数据的顺序是相反的。
以上的需求我们通过,删除acceptStack栈中的数据,在outputStack中添加这个数据,那么先在acceptStack中删除的数据,就会进入到outputStack的栈底,后在acceptStack中删除的数据,会后进入outputStack,那么它就会先出来。
那么两个栈,这样来合作,就会实现队列的先进先出,如图:1 是先进的(栈1) 那么1 就会先出来(栈2)。
进而实现了 题目的需求。
在pop 的方法中,如果说 self.outputStack 是空 没有数据,那么 就给它 while 循环我们的 作为添加数据的栈
acceptStack,删除这个栈中的内容,它会弹出,然后把它添加到 栈2 outputStack 中,它就会有数据,有数据的话就返回 (如果 调用了 删除 数据的这个方法的话)。如果说 做了循环,我们的栈2 outputStack 中还没有数据,就明 acceptStack 中,没有数据压入,也就说明这个 队列 没有添加数据,也就不会有删除的数据,所以返回一个None。
class Solution:
def init(self):
#添加数据栈
self.acceptStack=[]
#删除数据栈
self.outputStack = []
def push(self, node):
#向添加数据的栈中添加数据
self.acceptStack.append(node)
def pop(self):
#判断删除数据的栈中是否有数据,没有的话,就添加数据,添加数据时,要添加栈1 中删除的数据
if not self.outputStack:
while self.acceptStack:
self.outputStack.append(self.acceptStack.pop())
#如果有数据的话,就返回
if self.outputStack:
return self.outputStack.pop()
#如果没有数据,说明没有数据添加进去,也就不需要删除数据,所以返回none
else:
return None
二分查找法
分析查找:首先快速的查找方法 有二分查找法,那么什么是二分查找法?
二分查找法什么情况下用。有序的数组中。首先 肯定是在有序的 数组中的!!!!!
算法:二分法查找适用于数据量较大时,但是数据需要先排好顺序。主要思想是:(设查找的数组区间为array[low, high])
(1)确定该区间的中间位置K(2)将查找的值T与array[k]比较。若相等,查找成功返回此位置;否则确定新的查找区域,继续二分查找。区域确定如下:a.array[k]>T 由数组的有序性可知array[k,k+1,……,high]>T;故新的区间为array[low,……,K-1]b.array[k]<T 类似上面查找区间为array[k+1,……,high]。每一次查找与中间值比较,可以确定是否查找成功,不成功当前查找区间将缩小一半,递归查找即可。
时间复杂度为:O(log2n)。
时间复杂度
1.最坏情况查找最后一个元素(或者第一个元素)Master定理T(n)=T(n/2)+O(1)所以T(n)=O(log2n)
2.最好情况查找中间元素O(1)查找的元素即为中间元素(奇数长度数列的正中间,偶数长度数列的中间靠左的元素)
空间复杂度
- S(n)=n
二分法代码实现:
def BinarySearch(array,target):
left= 0
right= len(array)-1
while left <= right :
#除法没有移位的快
# mid = (left + right)//2
# 101 = 5 => 10 = 2
#1100 = 12 => 110 = 6
#一下用了 向右 移一位, 那么上面是解释,它就相当于 除以2 。
mid = (left + right) >> 1
#如果中间的数等于我们要找的数,那么就返回。
if array[mid] == target:
return mid
#如果说中间的数 < 目标的数,那么就说明,我们要找的数在右侧,所以左侧取值的索引需要改变为中间的索引+1;
elif array[mid]< target:
left = mid + 1
#如果说中间的数 > 目标的数,那么就说明,我们要找的数在左侧,所以左侧取值的索引需要改变为中间的索引-1; 因为越往左索引值越小
else:
right = mid-1
return None
把数组内的数据一分为二,然后计算出中间数据的 索引值。
数组中 最左侧的 索引为 0 ;最右侧的索引为 len(array)-1,数组的长度 减 1 就是 最后一个数的索引。
先判断中间索引的所对应的数组中的数值,是否与我们要查找的数字 target 相等,如果相等那么就返回,如果不相等,那么就继续判断。如果说我们找到的 array[mid] 小于 target 这个数; 那么 就说明 我们要查找的数在右侧的一半数据中,那么这个时候我们就需要改变我们左边的索引值,不在从0 开始,而是从我们中间 mid 的下一个开始,left = mid + 1,继续查找。如果说我们找到的 array[mid] 大于 target 这个数 ,那么就说明我们要查找的数据在左侧,这个时候就需要改变右侧的索引,为 right = mid-1,越往左侧走,索引值越小。直到找的的数 与target 相等为止。
以上为二分法的原理。
2. 旋转数组的最小数字 [^本题考点 查找]
把一个数组最开始的若干个元素搬到数组的末尾,我们称之为数组的旋转。 输入一个非减排序的数组的一个旋转,输出旋转数组的最小元素。 例如数组{3,4,5,1,2}为{1,2,3,4,5}的一个旋转,该数组的最小值为1。 NOTE:给出的所有元素都大于0,若数组大小为0,请返回0。
class Solution:
def minNumberInRotateArray(self, rotateArray):
#最小值 一定比前面的要小
# 二分法查找数据 找左右的方法是:
#右边的值大于中值,就说明最小值在左边
if not rotateArray:
return 0
left = 0
right = len(rotateArray) - 1
while left <= right:
mid = (left + right) >> 1
#如果说中间的数的上一个数 > 中间数,那么就说明,我们要找的数就是这个中间的数,返回这个数。
if rotateArray[mid - 1] > rotateArray[mid]:
return rotateArray[mid]
#如果说中间的数 < 中间数的上一个数,那么就说明,我们要找的数在二分法的左侧,所以右侧取值的索引需要改变为中间的索引-1;因为越往左索引值越小
elif rotateArray[mid] < rotateArray[right]:
right = mid - 1
#否则就说明,我们要找的数在二分法的右侧,所以左侧取值的索引需要改变为中间的索引+1;因为越往右索引值越小
else:
left = mid + 1
return 0
什么叫做数组?
所谓数组,是有序的元素序列。 [1] 若将有限个类型相同的变量的集合命名,那么这个名称为数组名。组成数组的各个变量称为数组的分量,也称为数组的元素,有时也称为下标变量。用于区分数组的各个元素的数字编号称为下标。数组是在程序设计中,为了处理方便, 把具有相同类型的若干元素按无序的形式组织起来的一种形式。 [1] 这些无序排列的同类数据元素的集合称为数组。
例如:
int (32 位) int int 这三个就会组成一个数组,类型相同的变量。
a(0) a(1) a(2)
数组与python中的 列表比较相似, 用索引去查找。
数组的长度是固定的,在初始化时就指定长度。列表是可以动态增加的。
数组还和元组比较像,元组是初始化后,长度指定了就不可以变。
但是元组在初始化时给的值,确定了以后就不可以变了。
所以可以理解为数组与list 列表很相似。
3.在二维数组中的查找[^本题考点 查找]
在一个二维数组中(每个一维数组的长度相同),每一行都按照从左到右递增的顺序排序,每一列都按照从上到下递增的顺序排序。请完成一个函数,输入这样的一个二维数组和一个整数,判断数组中是否含有该整数。
class Solution:
# array 二维列表
def Find(self, target, array):
# write code here
# 1 2 3 4
# 3 4 5 6
# 4 6 8 10
# 9 11 13 15
#时间复杂度 o(n**n)
# for i in range(len(array)):
# for j in range(len(array[i])):
# if target == array[i][j]:
# return True
# return False
#时间复杂度
#O(n)
#这个二维数组的长度是多少,也就是说这个数组有几行;
row_count = len(array)
i = 0
#这个数组列数的索引值,就是我们数组取第一个数的个数,也就是有几列
column_count = len(array[0])
#给j 一个值,就是数组列数的值-1,即为j 的最大值。
j = len(array[0])-1
#循环,当i 小于我们行数的时候,并且j 也没有取到 0 那么就进入循环,去查找数据。
#我们要取到每行的最后一个数,即对应的那一列的第一个数,来与我们的目标数来对比,这个数是这一行的最大数,是这一列的最小数。
while i < row_count and j >= 0:
#根据两个索引下标可以取到 对应的在数组中的值
value = array[i][j]
#如果说取到的值,刚好等于目标值,那么就说明我们找到了它,直接返回就好。
if value == target:
return True
#如果说取到的值 > 我们的目标值。那就说明它不在它所在的那一列里,因为这个数是那一列的最小值,这个时候就需要改变我们列的索引值,给它减-1,找前一列的数做比较
elif target < value:
j -= 1
#如果说取到的值 < 我们的目标值。那就说明它不在它所在的那一行里,因为这个数是那一行的最大值,这个时候就需要改变我们行的索引值,给它加+1,找下一行的数做比较
else:
i += 1
return False
4.包含min 函数的栈[^本题考点 栈]
定义栈的数据结构,请在该类型中实现一个能够得到栈中所含最小元素的min函数(时间复杂度应为O(1))。
原理:用空间换时间,用时间换空间;增加空间来减少时间的消耗
#第一种方法:考虑两个栈的长度相同,添加一个,另一个栈也会删除一个
class Solution:
#给这个类一个初始的属性,有一个栈,另外有一个最小值的列表栈
def __init__(self):
self.stack = []
self.minValue = []
#给栈中推进去数值,推进去元素node,添加函数
def push(self, node):
self.stack.append(node)
#如果最小值列表里有值
if self.minValue:
#如果最小值列表里的最后一个值 大于 node 这个值,说明node这个值小,
# 那么就放进最小值列表中;
if self.minValue[-1] > node:
self.minValue.append(node)
#如果列表里面的最后一个值,小于node值,那么就说明node这个值大;那么就添加上次添加进来的那个小的值,与栈中的数据长度保持一致;
else:
self.minValue.append(self.minValue[-1])
#如果最小值列表里面没有值,就在最小值列表里添加node
else:
self.minValue.append(node)
#给栈中做删除操作
def pop(self):
#如果说栈中是空值得话那么就返回none,说明没有在栈中压值进来,没有最小值
if self.stack == []:
return None
#栈的长度与最小值的栈的长度要相同,所以最小值列表也需要删除一个
self.minValue.pop()
#有值得话,就需要删除一个,删除做pop 操作;返回我们删除的那个数
return self.stack.pop()
#栈顶
def top(self):
#如果栈里没有数值的话,就返回一个空
if not self.stack:
return None
#否则栈里有数,那么就返回栈顶的那个数
return self.stack[-1]
#取出最小值,那么就是我们minvalue 中的最后一个值为最小值
def min(self):
#如果为空的话,就说明没有值,返回none
if self.minValue == []:
return None
return self.minValue[-1]
#第二种方法:不考虑两个栈的长度必须要保持一致,那么在栈删除值的时候,判断一下删除的值,是不是与装最小值的栈里的最后一个最小值相同,如果相同就删掉,如果不同,就不删除。
class Solution:
def __init__(self):
self.stack = []
self.minValue = []
def push(self, node):
# write code here
self.stack.append(node)
if self.minValue:
#如果最小值列表里的最后一个值 大于 node 这个值,说明node这个值小,
# 那么就放进最小值列表中;
if self.minValue[-1] > node:
self.minValue.append(node)
#最后一个值不大于node这个值得话;不做操作,不需要把它两个做的长度一致
else:
self.minValue.append(node)
def pop(self):
if self.stack == []:
return None
# write code here
#删除的时候,做个判断,它是不是与栈里面的最后一个值,与我们最小值栈里的最后一个值相等,那么就删除双方的这个值
if self.stack[-1] == self.minValue[-1]:
self.minValue.pop()
return self.stack.pop()
#如果不等的话,就只要删除栈 里最后一个值就可以
else:
return self.stack.pop()
def top(self):
if self.stack == []:
return None
return self.stack[-1]
# write code here
def min(self):
if self.minValue == []:
return None
return self.minValue[-1]
5.替换空格[^本题考点 字符串]
请实现一个函数,将一个字符串中的每个空格替换成“%20”。例如,当字符串为We Are Happy.则经过替换之后的字符串为We%20Are%20Happy。
# -*- coding:utf-8 -*-
class Solution:
# s 源字符串
def replaceSpace(self, s):
#第一种:python中自带的一个替换的函数
# return s.replace(' ','%20')
#第二种遍历来替换字符串中的空格
strlen = len(s)
#借助第三方的列表来实现时间的节省。
aaa = []
for i in range(strlen):
#如果是空格的话那就替换为%20.
if s[i] == " ":
#if s[i] isspace:
aaa.append("%")
aaa.append("2")
aaa.append("0")
else:
aaa.append(s[i])
return "".join(aaa)
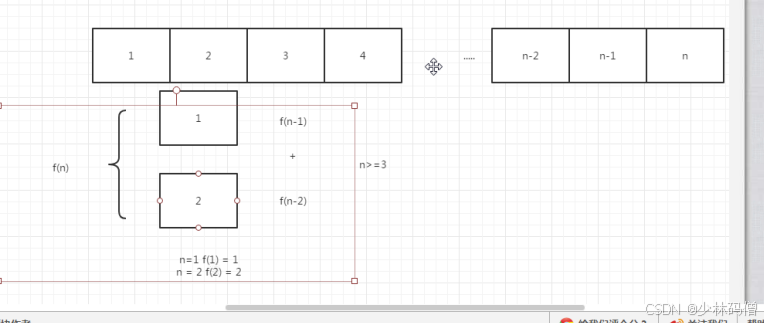
6.斐波那契数列
大家都知道斐波那契数列,现在要求输入一个整数n,请你输出斐波那契数列的第n项(从0开始,第0项为0)。n<=39
#第一种方法:下面是使用了for循环,
class Solution:
def Fibonacci(self, n):
# 如果是按照递归来写的话, 时间复杂度就是随着n的变化 增长率是 2^n
''' 递归实现
# n = 0 f(0) = 0
if n == 0:
return 0
# n = 1 f(1) = 1
if n == 1:
return 1
# if n > 1 f(n) = f(n-1) + f(n-2)
if n > 1:
num = self.Fibonacci(n-1) + self.Fibonacci(n-2)
return num
return None
'''
# n = 0 f(0) = 0
if n == 0:
return 0
# n = 1 f(1) = 1
if n == 1:
return 1
a = 1
b = 0
# if n > 1 f(n) = f(n-1) + f(n-2)
# h = a + b
# 当 n = 2 h = 0 + 1
ret = 0
#三个变量,互相转换 来实现
for i in range(0, n - 1):
ret = a + b
b = a
a = ret
return ret
#第二种方法:相对来说比较简便,简单来讲,就是取出这个列表的最后两项求和,就是列表的第三项,时间复杂度比较小,空间复杂度为 n
class Solution:
def Fibonacci(self, n):
#初始列表值 为 0 1 第三项为 0+1 = 1;
res = [0, 1, 1]
#临界条件为:第 n 项,所以就是 这个 列表的长度要小于等于 n;大于 n 就应该跳出这个循环。
while len(res) <= n:
#取出列表的最后两项,然后求和,并添加到列表中。
res.append(res[-1] + res[-2])
return res[n]
7.青蛙跳台阶
一只青蛙一次可以跳上1级台阶,也可以跳上2级。求该青蛙跳上一个n级的台阶总共有多少种跳法(先后次序不同算不同的结果)。
"""
1 (1)
2 (11,2)
3 (12,21,111)
4 (1111,22,112,121,211)
5 (11111,221,212,122,1121,2111,1112,1211)
6 (111111,222,2211,1122,2112,1221,2121,1212,21111,12111,11211,11121,11112,)
"""
class Solution:
def jumpFloor(self, number