此博客停止更新迁移至SnailDove’s Blog,查看本文点击此处
笔记源自:清华大学公开课:线性代数2——第11讲:计算机图像
提示:如果文中图片看不清文字,请右键单击鼠标,选择在新窗口打开图片,然后放大图片(这边上传之前都是可以看清的,由于网页正文部分大小固定,因此图片被自动缩小以便适配网页)。
引言
熟悉的三维空间的基本变换是:平移(translation),伸缩(rescaling),旋转(rotation),投影(projection)和反射(reflection)。现在一个问题:平移变换只对于点才有意义,因为平移变换会改变点的坐标,可是普通向量没有位置概念,只有大小和方向。那如何区分点和向量呢?这时候引入齐次坐标系(homogeneous coordinate system)。
对于任意一个3维空间点 p p 的坐标均是参照(相对于)基点(原点)的坐标,可以表示成,然而 op→=xe⃗ 1+ye⃗ 2+ze⃗ 3 o p → = x e → 1 + y e → 2 + z e → 3 是不参照任何东西的,为了在线性代数中统一表示和区分,把 p=⎛⎝⎜⎜⎜1000010000100000⎞⎠⎟⎟⎟⎛⎝⎜⎜⎜xyz1⎞⎠⎟⎟⎟op→=⎛⎝⎜⎜⎜1000010000100000⎞⎠⎟⎟⎟⎛⎝⎜⎜⎜xyz0⎞⎠⎟⎟⎟ p = ( 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 0 ) ( x y z 1 ) o p → = ( 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 0 ) ( x y z 0 ) , 这时三维空间中的一个点的齐次坐标是 (x,y,z,1) ( x , y , z , 1 ) 或 ⎛⎝⎜⎜⎜xyz1⎞⎠⎟⎟⎟ ( x y z 1 ) ,一个向量的齐次坐标是 (x,y,z,0) ( x , y , z , 0 ) 或 ⎛⎝⎜⎜⎜xyz0⎞⎠⎟⎟⎟ ( x y z 0 ) ,所以平移变换就不是 R3→R3 R 3 → R 3 。
定义 一个函数 f:Rn→RN f : R n → R N 是一个刚体运动(rigid motion),如果 ∀v,w∈Rn,||f(v)−f(w)||=||v−w|| ∀ v , w ∈ R n , | | f ( v ) − f ( w ) | | = | | v − w | | ,即内部的各点间距离不变。定理 R3 R 3 上的刚体运动是平移,旋转和反射的合成。此时, f(v)=Av+v0 f ( v ) = A v + v 0 ,其中 A A 是三阶正交阵。三阶正交阵的分类:设是一个三阶正交阵,则存在实可逆阵 P P ,,其中 P=(α1,α2,α3) P = ( α 1 , α 2 , α 3 ) ,根据相似的性质: |B|=±1→|A|=±1 | B | = ± 1 → | A | = ± 1 , A A 本身是一个正交阵,因此。
若 B33=1,AP=PB→Aα3=α3 B 33 = 1 , A P = P B → A α 3 = α 3 是一个旋转矩阵,旋转轴是 α3 α 3 所在直线,旋转角度是沿 α3 α 3 方向逆时针转 θ θ 角;若 B33=−1,AP=PB→Aα3=−α3 B 33 = − 1 , A P = P B → A α 3 = − α 3 是 A A 将变为 −α3 − α 3 ,将 α1,α2 α 1 , α 2 所在平面逆时针旋转 θ θ 角,此时 A A <script type="math/tex" id="MathJax-Element-32">A</script>的作用就是镜面反射和旋转,这里镜面指的是x-y平面。
平移translation
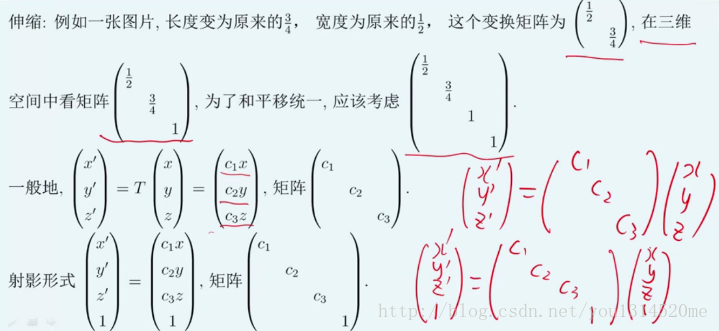
伸缩rescaling
旋转rotation
3个特殊情形
一般情形
旋转的性质
投影projection
反射