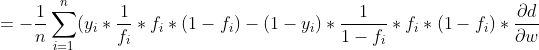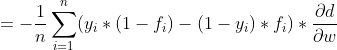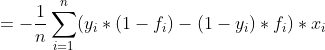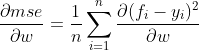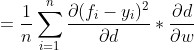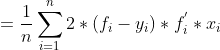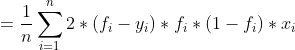本文将从KL距离(相对熵)、交叉熵、损失函数和一些公式推导来阐述逻辑回归这个传统的机器学习方法,重理论轻代码。
1.KL距离
KL距离又称作相对熵,通常是用来衡量两分布之间的相似度。公式如下:
其中P,Q是两分布。很显然,KL距离不具有对称性,正是因为这点,描述一些概率性问题的差异性通常使用KL距离,而不用欧式距,逻辑回归也是。
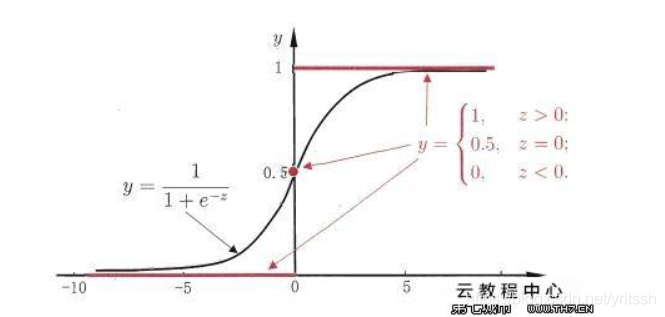
2.Sigmoid函数:
图像如下(网上百度的):
其中wx+b是线性函数,Sigmoid行数的作用就是将线性函数wx+b得到的结果映射到(0,1)之间的一个数,并且具有概率意义。
接下来求下Sigmoid函数的导数,后面会用到。
其中 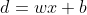
3.逻辑回归损失函数
文章开头提到过,KL距离通常用来衡量概率之间的相似度,经过Sigmoid函数转换,我们最终得到的一个值正好是一个概率值。又因为逻辑回归是个二分类问题,可以认为有两种类别0和1,假设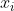
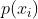
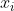
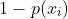
![d_{KL} = \frac{1}{n}\sum_{i=1}^{n}[y_{i}*log\frac{y_{i}}{f_{i}} + (1-y_{i})*log\frac{1-y_{i}}{1-f_{i}}]](/image/aHR0cHM6Ly9pLWJsb2cuY3NkbmltZy5jbi9ibG9nX21pZ3JhdGUvNDI3M2VkODEwYzdmOWEzNDNjOTY2ZjhjZWY3NGNjOWUuZ2lm)
其中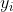
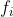
其中
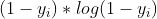
机器学习训练的过程,就是不断更新 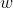

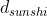
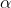
回到逻辑回归中,它的损失函数是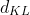
接下来我们看下 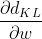
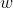
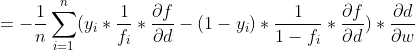
在前面我们对 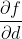

我们将点 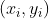
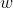
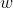
首先,假设我们用mse来做损失函数,那么
我们结合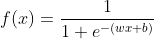

我们从sigmoid函数中可以看出,当我们把 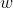
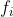
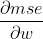
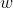
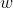
4.数据归一化
我们接着观察
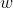
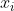
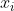
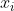
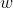
- 离差标准化,是对原始数据的线性变换,使结果值映射到[0 - 1]之间,转换公式
,其中的min是数据集中最小值,max是数据集中最大值,因为处理后的
都是大于0的,故
只会往同一个方向走
- Z-score标准化方法, 这种方法给予原始数据的均值(mean)和标准差(standard deviation)进行数据的标准化。经过处理的数据符合标准正态分布,即均值为0,标准差为1,转化函数为:
,其中
是数据集的均值,
是数据集的标准差。因为处理后的
有正有负,那么
不一定会沿着同一方向走,这样会使得训练过程时间大大减少。
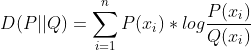
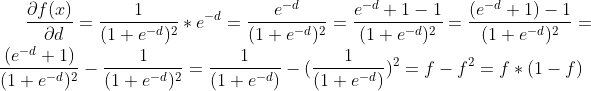
![d_{KL} =\frac{1}{n} \sum_{i=1}^{n}[y_{i}*logy_{i}-y_{i}*logf_{i}+(1-y_{i})*log(1-y_{i})-(1-y_{i})*log(1-f_{i})]](/image/aHR0cHM6Ly9pLWJsb2cuY3NkbmltZy5jbi9ibG9nX21pZ3JhdGUvOGRiYTViNmU0YTJmMjYzM2ZlZDQyZjU2NTM2NjIzOWEuZ2lm)
![d_{KL} = -\frac{1}{n}\sum_{i=1}^{n}[y_{i}*logf_{i}+(1-y_{i})*log(1-f_{i})]](/image/aHR0cHM6Ly9pLWJsb2cuY3NkbmltZy5jbi9ibG9nX21pZ3JhdGUvZDM3ZjY4YzJkODUwNDk5MzQ3MWRkZGY5NzI0NjU5YjUuZ2lm)


![=\frac{\partial (-\frac{1}{n}\sum_{i=1}^{n}[y_{i}*logf_{i}+(1-y_{i})*log(1-f_{i})])}{\partial d} *\frac{\partial d}{\partial w}](/image/aHR0cHM6Ly9pLWJsb2cuY3NkbmltZy5jbi9ibG9nX21pZ3JhdGUvZWFhNDcwYmUxY2FmMmFkMGExZGFjODlhYWQ1ZWI3YTAuZ2lm)