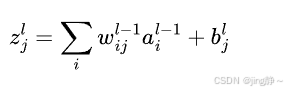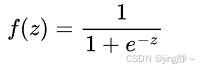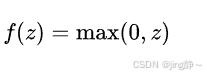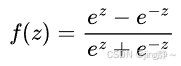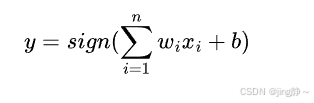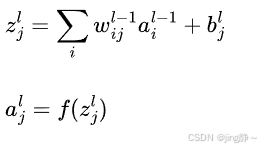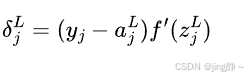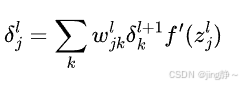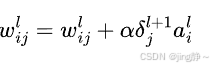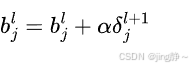【大数据】机器学习------神经网络模型

一、神经网络模型

1. 基本概念
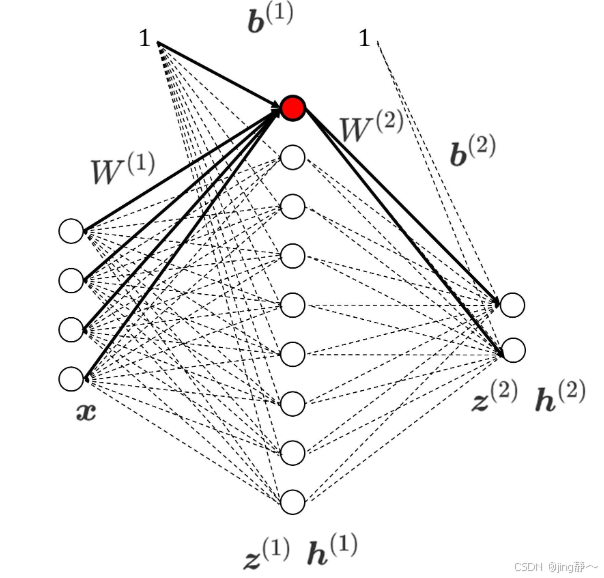
神经网络是一种模拟人类大脑神经元结构的计算模型，由多个神经元（节点）组成，这些节点按照不同层次排列，通常包括输入层、一个或多个隐藏层和输出层。每个神经元接收来自上一层神经元的输入，通过加权求和和激活函数处理后将结果传递给下一层。

在这里插入图片描述

2. 数学公式
对于一个具有 $L$ 层的神经网络，第 $l$ 层第 $j$ 个神经元的输入 $z_j^l$ 可以表示为：
在这里插入图片描述

其中 $w_{ij}^{l-1}$ 是第 $l - 1$ 层第 $i$ 个神经元到第 $l$ 层第 $j$ 个神经元的连接权重， $a_i^{l-1}$ 是第 $l - 1$ 层第 $i$ 个神经元的输出（激活值）， $b_j^l$ 是第 $l$ 层第 $j$ 个神经元的偏置。

激活函数 $a_j^l = f(z_j^l)$ ，常见的激活函数有：

Sigmoid 函数：
ReLU 函数：
Tanh 函数：

二、感知机与多层网络

1. 感知机
感知机是一种最简单的神经网络，可用于二分类任务。对于输入向量 $\mathbf{x}=(x_1,x_2,\cdots,x_n)$ ，感知机的输出为：
在这里插入图片描述

其中 (sign) 函数为符号函数，当 (z\geq0) 时，(sign(z)=1)；当 (z<0) 时，(sign(z)=-1)。

2. 多层感知机（MLP）
多层感知机包含多个隐藏层，能够解决非线性可分问题。

代码示例：感知机

import numpy as np


class Perceptron:
    def __init__(self, input_size, learning_rate=0.01, epochs=100):
        self.weights = np.random.rand(input_size)
        self.bias = np.random.rand(1)
        self.learning_rate = learning_rate
        self.epochs = epochs

    def activation(self, z):
        return 1 if z >= 0 else -1

    def predict(self, x):
        linear_output = np.dot(x, self.weights) + self.bias
        return self.activation(linear_output)

    def train(self, X, y):
        for _ in range(self.epochs):
            for x, label in zip(X, y):
                prediction = self.predict(x)
                update = self.learning_rate * (label - prediction)
                self.weights += update * x
                self.bias += update


# 示例数据
X = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
y = np.array([-1, -1, -1, 1])

# 初始化感知机
perceptron = Perceptron(input_size=2)

# 训练感知机
perceptron.train(X, y)

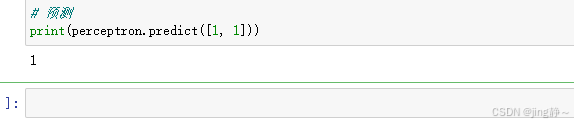
# 预测
print(perceptron.predict([1, 1]))

在这里插入图片描述

代码解释：

__init__ 方法初始化感知机的权重、偏置、学习率和训练轮数。
activation 是激活函数，这里使用简单的符号函数。
predict 计算感知机的输出。
train 方法根据训练数据更新权重和偏置。

三、误差逆传播算法（BP 算法）

BP 算法用于训练多层神经网络，通过计算输出误差并将其反向传播更新权重和偏置。

1. 前向传播
计算每层的输入和输出：
在这里插入图片描述

2. 反向传播
计算输出层误差：
在这里插入图片描述

对于隐藏层：
在这里插入图片描述

权重更新公式：
在这里插入图片描述

偏置更新公式：
在这里插入图片描述

代码示例：BP 算法实现

import numpy as np


def sigmoid(z):
    return 1 / (1 + np.exp(-z))


def sigmoid_derivative(z):
    return sigmoid(z) * (1 - sigmoid(z))


class NeuralNetwork:
    def __init__(self, input_size, hidden_size, output_size):
        self.input_size = input_size
        self.hidden_size = hidden_size
        self.output_size = output_size
        self.weights_input_hidden = np.random.rand(self.input_size, self.hidden_size)
        self.weights_hidden_output = np.random.rand(self.hidden_size, self.output_size)
        self.bias_hidden = np.random.rand(self.hidden_size)
        self.bias_output = np.random.rand(self.output_size)

    def forward(self, x):
        self.z_hidden = np.dot(x, self.weights_input_hidden) + self.bias_hidden
        self.a_hidden = sigmoid(self.z_hidden)
        self.z_output = np.dot(self.a_hidden, self.weights_hidden_output) + self.bias_output
        self.a_output = sigmoid(self.z_output)
        return self.a_output

    def backward(self, x, y, learning_rate):
        # 计算输出层误差
        output_error = y - self.a_output
        output_delta = output_error * sigmoid_derivative(self.z_output)
        # 计算隐藏层误差
        hidden_error = np.dot(output_delta, self.weights_hidden_output.T)
        hidden_delta = hidden_error * sigmoid_derivative(self.z_hidden)
        # 更新权重和偏置
        self.weights_hidden_output += learning_rate * np.outer(self.a_hidden, output_delta)
        self.bias_output += learning_rate * output_delta
        self.weights_input_hidden += learning_rate * np.outer(x, hidden_delta)
        self.bias_hidden += learning_rate * hidden_delta


# 示例数据
X = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
y = np.array([[0], [1], [1], [0]])

# 初始化神经网络
nn = NeuralNetwork(input_size=2, hidden_size=2, output_size=1)

# 训练
for epoch in range(10000):
    for x, target in zip(X, y):
        nn.forward(x)
        nn.backward(x, target, learning_rate=0.1)


# 预测
print(nn.forward([1, 1]))
```![在这里插入图片描述](https://i-blog.csdnimg.cn/direct/65389eb31fe24fbea5bf766e92472d30.png)

**代码解释**：
- `sigmoid` 和 `sigmoid_derivative` 函数分别计算 sigmoid 函数及其导数。
- `NeuralNetwork` 类包含初始化权重和偏置、前向传播和反向传播的方法。
- `forward` 计算网络的输出。
- `backward` 计算误差并更新权重和偏置。


**四、全局最小与局部最小**

**1. 概念**
- **全局最小**：在整个参数空间中，损失函数达到的最小点。
- **局部最小**：在参数空间的某个局部区域内，损失函数达到的最小点，但不是全局最小。

**2. 解决方法**
- 随机初始化权重。
- 使用模拟退火等算法。


**五、其他常见神经网络**

**1. 卷积神经网络 (CNN)**
主要用于图像处理，利用卷积层提取特征，通过池化层降低维度。

**代码示例：使用 Keras 实现 CNN**
```python
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Conv2D, MaxPooling2D, Flatten, Dense
import numpy as np


# 构建简单的 CNN 模型
model = Sequential([
    Conv2D(32, (3, 3), activation='relu', input_shape=(28, 28, 1)),
    MaxPooling2D((2, 2)),
    Flatten(),
    Dense(10, activation='softmax')
])


# 编译模型
model.compile(optimizer='adam', loss='sparse_categorical_crossentropy', metrics=['accuracy'])


# 示例数据
X = np.random.random((100, 28, 28, 1))
y = np.random.randint(0, 10, (100,))


# 训练模型
model.fit(X, y, epochs=10)

代码解释：

Conv2D 是卷积层，MaxPooling2D 是池化层，Flatten 将多维数据展平，Dense 是全连接层。
model.compile 配置模型的优化器和损失函数。
model.fit 进行模型训练。

2. 循环神经网络 (RNN)
适用于序列数据，如文本、时间序列，通过隐藏状态保存序列信息。

代码示例：使用 Keras 实现 RNN

from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import SimpleRNN, Dense
import numpy as np


# 构建简单的 RNN 模型
model = Sequential([
    SimpleRNN(50, activation='relu', input_shape=(10, 1)),
    Dense(1)
])


# 编译模型
model.compile(optimizer='adam', loss='mse')


# 示例数据
X = np.random.random((100, 10, 1))
y = np.random.random((100, 1))


# 训练模型
model.fit(X, y, epochs=10)

代码解释：

SimpleRNN 是简单循环神经网络层。
其余部分与 CNN 示例类似，包括模型的编译和训练。

六、深度学习
深度学习是使用具有多个层次的神经网络进行学习的技术，通过大量数据和强大的计算能力训练复杂的网络结构，在图像识别、语音识别、自然语言处理等领域取得了巨大成功。

通过以上内容，你可以对神经网络的各个知识点有一个全面的了解，包括基本的数学公式、不同类型神经网络的实现代码，以及如何使用流行的深度学习框架（如 Keras）进行模型的构建和训练。不同的网络结构和算法可以根据具体的任务和数据特点进行选择和优化，以达到更好的性能。

【大数据】机器学习------神经网络模型

悦读