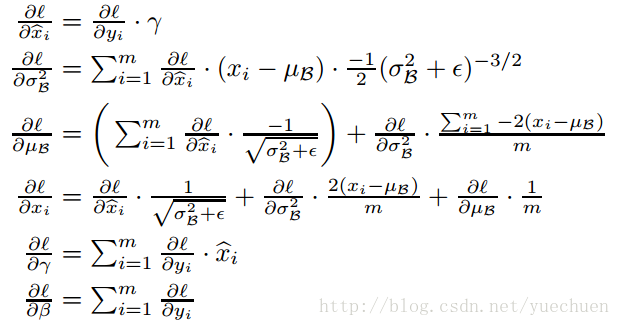Batch Normalization梯度反向传播推导

最近在看CS231N的课程，同时也顺带做配套的作业，在Assignment2 中关于Batch Normalization的具体数学过程则困惑了很久，通过参看一些博客自己推导了一遍，供大家参考。

Batch Normalization

首先，关于Batch Normalization的具体实现过程就不在此介绍了，想了解的可以参看论文或者博客。
对于Batch Normalization的前向传播可以参看下图的过程，它主要思路就是将每个Batch的输入根据均值 $\mu_{B}$ 和方差 $^2_{B}$ 进行归一化，然后再进行尺度缩放到 $y_{i}$

对于前向传播网络，可以很直观的给出实现代码

def batchnorm_forward(x, gamma, beta, bn_param):
  """
  Input:
  - x: (N, D)维输入数据
  - gamma: (D,)维尺度变化参数 
  - beta: (D,)维尺度变化参数
  - bn_param: Dictionary with the following keys:
    - mode: 'train' 或者 'test'
    - eps: 一般取1e-8~1e-4
    - momentum: 计算均值、方差的更新参数
    - running_mean: (D,)动态变化array存储训练集的均值
    - running_var：(D,)动态变化array存储训练集的方差

  Returns a tuple of:
  - out: 输出y_i（N，D）维
  - cache: 存储反向传播所需数据
  """
  mode = bn_param['mode']
  eps = bn_param.get('eps', 1e-5)
  momentum = bn_param.get('momentum', 0.9)

  N, D = x.shape
  # 动态变量，存储训练集的均值方差
  running_mean = bn_param.get('running_mean', np.zeros(D, dtype=x.dtype))
  running_var = bn_param.get('running_var', np.zeros(D, dtype=x.dtype))

  out, cache = None, None
  # TRAIN 对每个batch操作
  if mode == 'train':
    sample_mean = np.mean(x, axis = 0)
    sample_var = np.var(x, axis = 0)
    x_hat = (x - sample_mean) / np.sqrt(sample_var + eps)
    out = gamma * x_hat + beta
    cache = (x, gamma, beta, x_hat, sample_mean, sample_var, eps)
    running_mean = momentum * running_mean + (1 - momentum) * sample_mean
    running_var = momentum * running_var + (1 - momentum) * sample_var
  # TEST：要用整个训练集的均值、方差
  elif mode == 'test':
    x_hat = (x - running_mean) / np.sqrt(running_var + eps)
    out = gamma * x_hat + beta
  else:
    raise ValueError('Invalid forward batchnorm mode "%s"' % mode)

  bn_param['running_mean'] = running_mean
  bn_param['running_var'] = running_var

  return out, cache

上述代码基于CS231N Assignment2，值得注意的是Batch Normalization对于在训练和测试阶段的计算方法不一样，因为训练阶段的均值和方差是基于一个Batch的数据，而测试阶段是基于整个训练集求得。

梯度反向传播

Batch Normalization最让人头疼的就是理清楚反向传播梯度并写成代码，当然它依然遵循链式求导法则。首先我们基于上图，将变量定义如下：

$\sigma$ 为一个batch所有样本的方差
$\mu$ 为样本均值
$\widehat {x}$ 为归一化后的样本数据
$y_{i}$ 为输入样本 $x_{i}$ 经过尺度变化的输出量
$\gamma$ 和 $\beta$ 为尺度变化系数
$\dfrac {\partial L} {\partial y}$ 为已知，并假设 $x$ 和 $y$ 都为（N，D）维，即有N个维度为D的样本

由于网络正向传播是根据 $\gamma$ $\beta$ 和 $\widehat {x}$ 将 $x_{i}$ 变换为 $y_{i}$ ，那么反向传播则是根据 $\dfrac {\partial L} {\partial y_{i}}$ 求得 $\dfrac {\partial L} {\partial\gamma}$ $\dfrac {\partial L} {\partial\beta}$ 和 $\dfrac {\partial L} {\partial x_{i}}$ 。

\partial L \partial γ = \sum i \partial L \partial y i \partial y i \partial γ = \sum i \partial L \partial y i x ˆ i

$\begin{align} \dfrac {\partial L} {\partial\gamma}&=\sum _{i}\dfrac {\partial L} {\partial y_{i}}\dfrac {\partial y_{i}} {\partial \gamma}\\ &=\sum _{i}\dfrac {\partial L} {\partial y_{i}}\widehat {x}_{i} \end{align}$

\partial L \partial β = \sum i \partial L \partial y i \partial y i \partial β = \sum i \partial L \partial y i

$\begin{align} \dfrac {\partial L} {\partial\beta}&=\sum _{i}\dfrac {\partial L} {\partial y_{i}}\dfrac {\partial y_{i}} {\partial \beta}\\ &=\sum _{i}\dfrac {\partial L} {\partial y_{i}} \end{align}$
上面两个式子都涉及到Batch中的N个样本的累加，因为N个样本的

yi $y_{i}$ 对

β $\beta$

γ $\gamma$ 都有影响。

直接求 $\dfrac {\partial L} {\partial x_{i}}$ 步骤比较长，不直观，且 $\mu(x)$ 、 $\sigma(x)$ 、 $\widehat {x}(x)$ ，因此我们首先求 $\dfrac {\partial L} {\partial \widehat {x}}$ 、 $\dfrac {\partial L} {\partial \mu}$ 和 $\dfrac {\partial L} {\partial \sigma}$ :

\partial L \partial x ˆ = \partial L \partial y \partial y \partial x ˆ = \partial L \partial y γ

$\begin{align} \dfrac {\partial L} {\partial \widehat {x}}&=\dfrac {\partial L} {\partial y}\dfrac {\partial y} {\partial \widehat {x}} \\ &=\dfrac {\partial L} {\partial {y}}\gamma \end{align}$

\partial L \partial σ = \sum i \partial L \partial y i \partial y i \partial x ˆ i \partial x ˆ i \partial σ = - 1 2 \sum i \partial L \partial x i ˆ (x i - μ) (σ + ε) - 1.5

$\begin{align} \dfrac {\partial L} {\partial \sigma}&=\sum _{i}\dfrac {\partial L} {\partial y_{i}}\dfrac {\partial y_{i}} {\partial \widehat {x}_{i}}\dfrac {\partial \widehat {x}_{i}}{\partial \sigma} \\ &=-\dfrac{1}{2}\sum _{i}\dfrac {\partial L} {\partial \widehat {x_{i}}}(x_{i}-\mu)(\sigma+\varepsilon)^{-1.5} \end{align}$

\partial L \partial μ = \partial L \partial x ˆ \partial x ˆ \partial μ + \partial L \partial σ \partial σ \partial μ = \sum i \partial L \partial x ˆ i - 1 σ + ε - - - - - \sqrt + \partial L \partial σ - 2 Σ i ( x i - μ ) N

$\begin{align} \dfrac {\partial L} {\partial \mu}&=\dfrac {\partial L} {\partial \widehat {x}}\dfrac {\partial \widehat {x}}{\partial \mu}+\dfrac {\partial L} {\partial \sigma}\dfrac {\partial \sigma}{\partial \mu} \\ &=\sum _{i}\dfrac {\partial L} {\partial \widehat {x}_{i}}\dfrac {-1}{\sqrt {\sigma+ \varepsilon}}+\dfrac {\partial L} {\partial \sigma}\dfrac {-2\Sigma _{i}\left( x_{i}-\mu\right) } {N} \end{align}$

下面，就可以求 $\dfrac {\partial L} {\partial x_{i}}$ 啦：

\partial L \partial x i = \partial L \partial x i ˆ \partial x i ˆ \partial x i + \partial L \partial σ \partial σ \partial x i + \partial L \partial μ \partial μ \partial x i = \partial L \partial x ˆ i 1 σ + ε - - - - - \sqrt + \partial L \partial σ 2 ( x i - μ ) N + \partial L \partial μ 1 N

$\begin{align} \dfrac {\partial L} {\partial x_{i}}&=\dfrac {\partial L} {\partial \widehat {x_{i}}}\dfrac {\partial \widehat {x_i}}{\partial x_{i}}+\dfrac {\partial L} {\partial \sigma}\dfrac {\partial \sigma}{\partial x_{i}}+\dfrac {\partial L} {\partial \mu}\dfrac {\partial \mu}{\partial x_{i}} \\ &=\dfrac {\partial L} {\partial \widehat {x}_{i}}\dfrac {1}{\sqrt {\sigma+ \varepsilon}}+\dfrac {\partial L} {\partial \sigma}\dfrac{2(x_i-\mu)}{N}+\dfrac {\partial L} {\partial \mu}\dfrac {1}{N} \end{align}$

在上面的式子中我写成 $\dfrac {\partial L} {\partial x_{i}}$ 而不是 $\dfrac {\partial L} {\partial x}$ 是为了方便理解，当然在代码中我们会表示成后者以提高计算速度。至此，我们就完成了Batch Normalization的梯度反向传播的全过程，并得到论文给出的结果：

这里写图片描述

下面，我们就根据上面的步骤来完成代码：

def batchnorm_backward(dout, cache):
  """
  Inputs:
  - dout: 上一层的梯度，维度(N, D)，即 dL/dy
  - cache: 所需的中间变量，来自于前向传播

  Returns a tuple of:
  - dx: (N, D)维的 dL/dx
  - dgamma: (D,)维的dL/dgamma
  - dbeta: (D,)维的dL/dbeta
  """
    x, gamma, beta, x_hat, sample_mean, sample_var, eps = cache
  N = x.shape[0]

  dgamma = np.sum(dout * x_hat, axis = 0)
  dbeta = np.sum(dout, axis = 0)

  dx_hat = dout * gamma
  dsigma = -0.5 * np.sum(dx_hat * (x - sample_mean), axis=0) * np.power(sample_var + eps, -1.5)
  dmu = -np.sum(dx_hat / np.sqrt(sample_var + eps), axis=0) - 2 * dsigma*np.sum(x-sample_mean, axis=0)/ N
  dx = dx_hat /np.sqrt(sample_var + eps) + 2.0 * dsigma * (x - sample_mean) / N + dmu / N

  return dx, dgamma, dbeta

附：两个有用的博客这里和这里