一：题目

给定一个数组 nums，有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。

返回滑动窗口中的最大值。

进阶：

你能在线性时间复杂度内解决此题吗？

示例:

输入: nums = [1,3,-1,-3,5,3,6,7], 和 k = 3
输出: [3,3,5,5,6,7] 

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/sliding-window-maximum
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

题目链接： https://leetcode-cn.com/problems/sliding-window-maximum

二：问题描述 

 这道题的暴力解法一眼就可以看出来，就是每三个数比较，最大的放入数组就好了，但这种方法要遍历整个数组并且每后移一个元素内部还要遍历k个元素比较大小。所以整体时间复杂度是O(nk)，不可取。

可以发现，上述解法的时间复杂度为O(nk)的主要原因是，重复计算了n(k-1)个数字。比如第一个窗口 [1,3,-1] 和第二个窗口  [3,-1,-3] ,重复计算了3和-1的大小，所以我们可以在次优化，让每两个数只比较一次。

可以采用双端队列的方式，来看采用双端队列的原因

每一个数入队列，都与队列内的位于队尾的数比较，如果大于队尾的数，则删掉队尾，直到队列为空或者不大于队尾元素，将此数插入队尾。

假设k=3，如图所示：

• 当1将入队列，队列为空，直接加入，此时队列头和队列尾都是1。
• 当3将入队列，发现大于队列尾部的1，则删除1，此时队列为空，3直接加入队列。
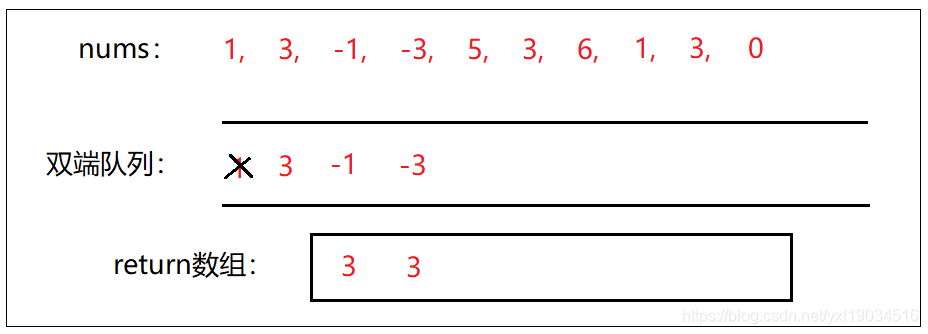
• 当-1将入队列，发现比队列尾部的3小，直接加入队列。此时达到窗口阈值，将队列头部的3入return数组。
• 当-3将入队列，发现比队列尾部的-1小，直接加入队列。此时达到窗口阈值，将队列头部的3入return数组。

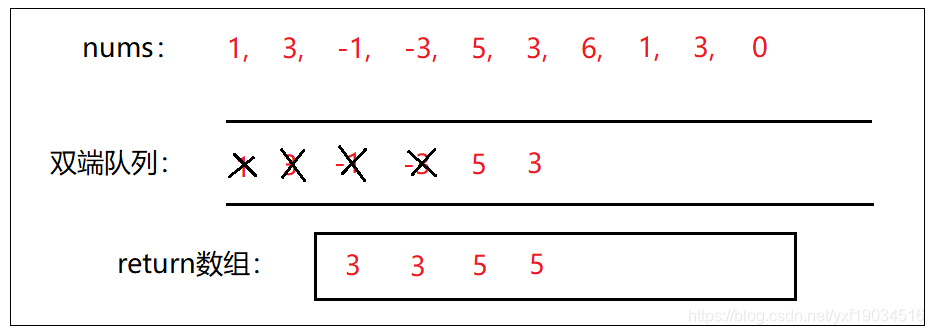
•  当5将入队列，从队列尾部依次比较，所以会删除-3，-1,3。将头部的5加入return数组。
•  当3将入队列，直接加入。依然将头部的5加入return数组。

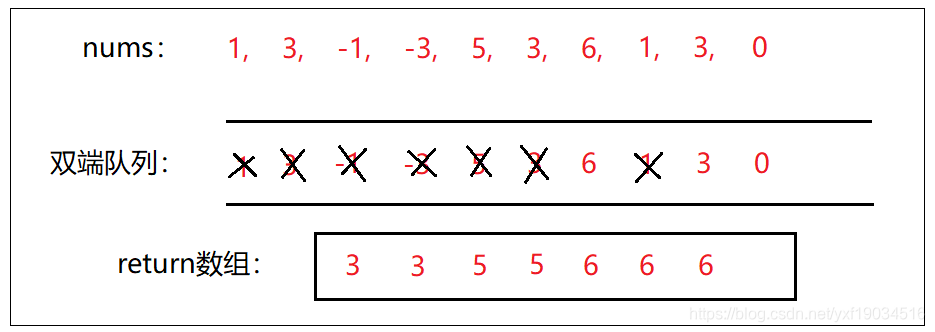
•  到这里问题就来了，当0入队列时，发现队列头部是6，所以将会把6加入到return数组的最后一个元素。但实际情况应该是3。
• 所以要考虑到，如果nums数组中有某一个最大的数，如果不对其处理的话，这个数将一直位于队列头部，那么后面return数组的元素将全部是这个最大数。
• 我们知道窗口大小k=3，所以6这个元素，其实根本跟[1,3,0]没有任何关系，我们可以判断当0元素的下标9，减去队列头部6元素的下标6，正好等于k的时候，就可以把队列头部的元素删掉。

 经过上面的分析，我们的逻辑 基本很清晰了，那么代码就信手拈来。但是有一个最重要的点，以上逻辑容易理解，但是我们用到了元素的下标，如果队列中放入的是元素本身，那么我们就无法取到下标。那么上述的0和6之间，就没有办法比较。

所以，我们队列中加入的应该是元素的下标。

三：代码

public int[] maxSlidingWindow(int[] nums, int k) {
        //先声明return数组
        int[] ret = new int[nums.length-k+1];
        //这里用到了LinkedList，前面的接口Deque就是双端队列，这个不是关键
        Deque<Integer> deque = new LinkedList<>();
        for (int i = 0; i < nums.length; i++) {
            //这里就是主要逻辑，当前元素是否大于队尾元素，如果大于就删除
            while (!deque.isEmpty() && nums[i] > nums[deque.getLast()]){
                deque.removeLast();
            }
            //如果不大于，或者队列为空了，则加入下标
            deque.addLast(i);
            //这里就是判断，两个下标差是否等于k，如果等于就删除头部
            if (i-deque.getFirst() == k){
                deque.removeFirst();
            }
            //这里说明什么时候将队列头加入return数组
            if (i-k+1 >=0){
                ret[i-k+1] = nums[deque.getFirst()];
            }
        }
        return ret;
    }

四：总结 

 总的来说，想到用双端队列解此题比较困难，其实真的想到了，那这个逻辑并不困难。主要一个拐弯的点就是队列里面应该放的是元素的下标。当然这个题的解法并不止这一种，也可以用大根堆来解决，后续用到了会做更新。