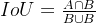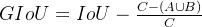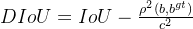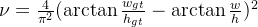YOLOv8完整网络结构详细介绍

一、整体网络预览

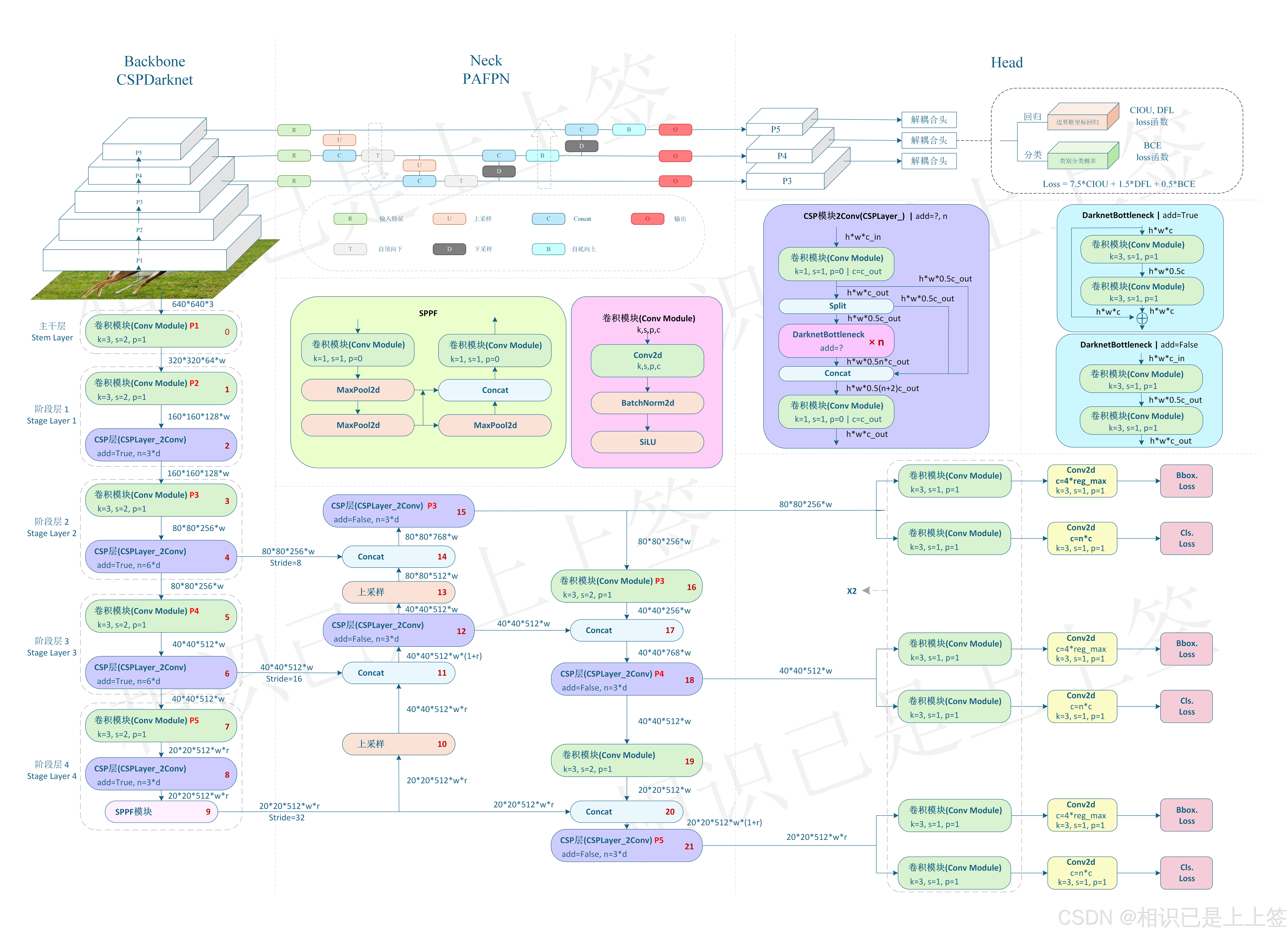
整体网络结构和以往的YOLOv4,v5等版本大致相同，由特征提取骨干Backbone、特征融合Neck以及回归分类Head组成。

和以往对比不同点是三个结构的细节模块，其特有的模块来体现出优越性。

二、特征提取骨干Backbone

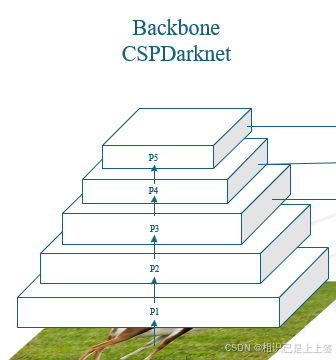
Backbone的作用是提取图像的详细信息特征，可以说是网络后续的根本。一个好的特征提取网络可以大大提升识别的效果和指标。举个例子说，经典的resnet50和近几年出现的Swin transformer网络对比，在目标检测任务中，map指标可以相差5%左右（仅改变Backbone网络，具体数据集具体测试，亲测）。

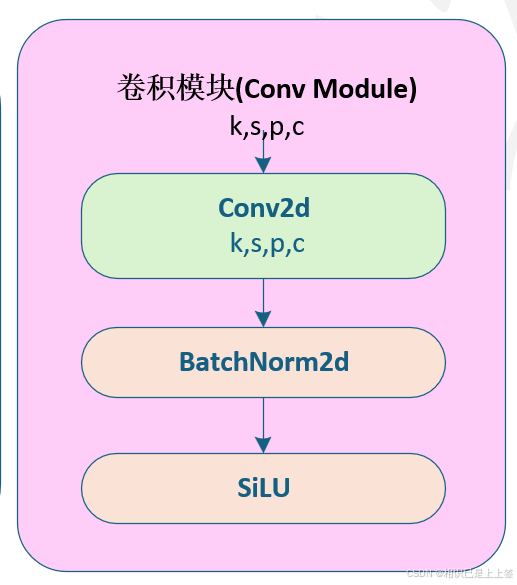
2.1 卷积模块（Conv Module）

卷积模块是由卷积-->归一化-->激活函数

卷积：使用 2D 卷积操作（nn.Conv2d），提取局部特征。

归一化：使用 Batch Normalization（nn.BatchNorm2d），加速训练和提高稳定性。

激活：使用非线性激活函数SiLU，引入非线性能力。

"""模块代码"""
import torch
import torch.nn as nn

class Conv(nn.Module):
    def __init__(self, in_channels, out_channels, kernel_size=3, stride=2, padding=1, groups=1):
        super(Conv, self).__init__()
        # 自动计算 padding
        self.padding = kernel_size // 2 if padding is None else padding
        # 定义卷积层
        self.conv = nn.Conv2d(in_channels, out_channels, kernel_size, stride, self.padding, groups=groups, bias=False)
        # 定义归一化层
        self.bn = nn.BatchNorm2d(out_channels)
        # 定义激活函数（SiLU / Swish）
        self.act = nn.SiLU()

    def forward(self, x):
        # 顺序执行：卷积 -> 归一化 -> 激活
        return self.act(self.bn(self.conv(x)))

if __name__ == '__main__':
    x = torch.randn(1, 3, 640, 640)  # Batch size=1, Channels=3, Height=640, Width=640
    conv = Conv(3, 64, kernel_size=3, stride=2)
    output = conv(x)
    print(output.shape)  # 输出形状：torch.Size([1, 64, 320, 320])

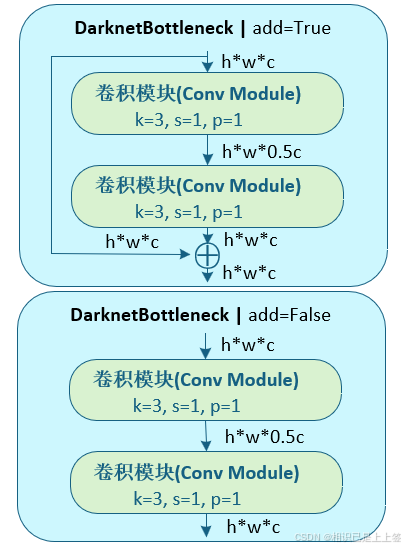
2.2 DarknetBottleneck模块

DarknetBottleneck模块包含两个卷积操作，但是分成了两个不同类型，根据add参数确定，若add为True，则引入残差连接。若为False，则直接进行简单的堆叠计算即可。

引入残差的模块通常用在骨干网络或特征提取模块中，而没有引入残差的模块适用于网络的起始部分（浅层网络）或特定的特征处理模块。

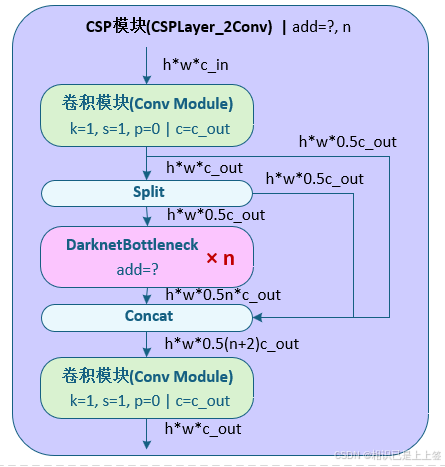
2.3 CSP模块(CSPLayer_2Conv)

CSPLayer_2Conv经过一个卷积模块引入一个残差连接，之后后分割为两部分一部分再进行一个残差连接，另一部分进入n个DarknetBottleneck模块，输出与两个残差进行Conact操作，最后进行一个卷积模块。

这样设计每个模块最多有两个卷积层，效率提高了很多。通过分支结构实现梯度和特征的高效流动，保留特征流动性。最重要的是可以通过调整通道数和卷积层数，适应不同网络深度需求。

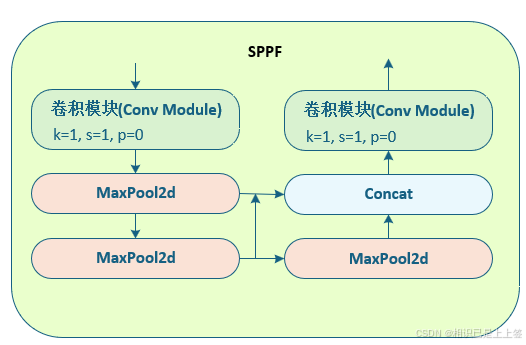
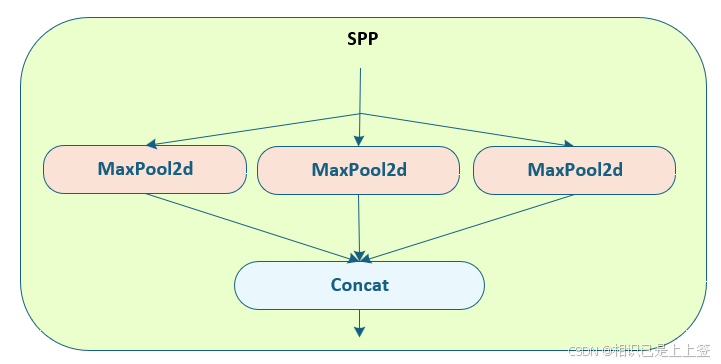
2.4 SPPF模块

SPPF模块是基于YOLOv5（yolov5 6.0之前）的SPP模块进行的改进。SPP是将三个并行的MaxPool和输入concat到一起，第一个MaxPool的kernel为5*5，第二个为9*9，第三个为13*13。SPPF，是将三个kernel为5*5的MaxPool做串行计算再进行残差链接最后进行Concat操作，减少了特征图的冗余计算，提高了推理速度。

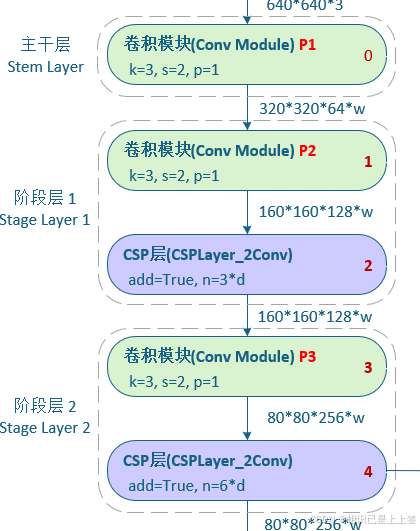
2.5 整个特征提取网络

YOLOv8的backbone网络是改进的CSPDarknet，从YOLOv4的CSPDarknet53，再到YOLOv5的CSPNet+Focus结构，最后到YOLOv8对CSPDarknet的改进。

可以看出YOLO各个版本都是基于CSPNet去做的，CSPNet跨阶段局部网络的优势在于解决大型卷积网络结构中的重复梯度问题，去减少模型参数和flops，这刚好与YOLO设计的初心适配，轻量快速。

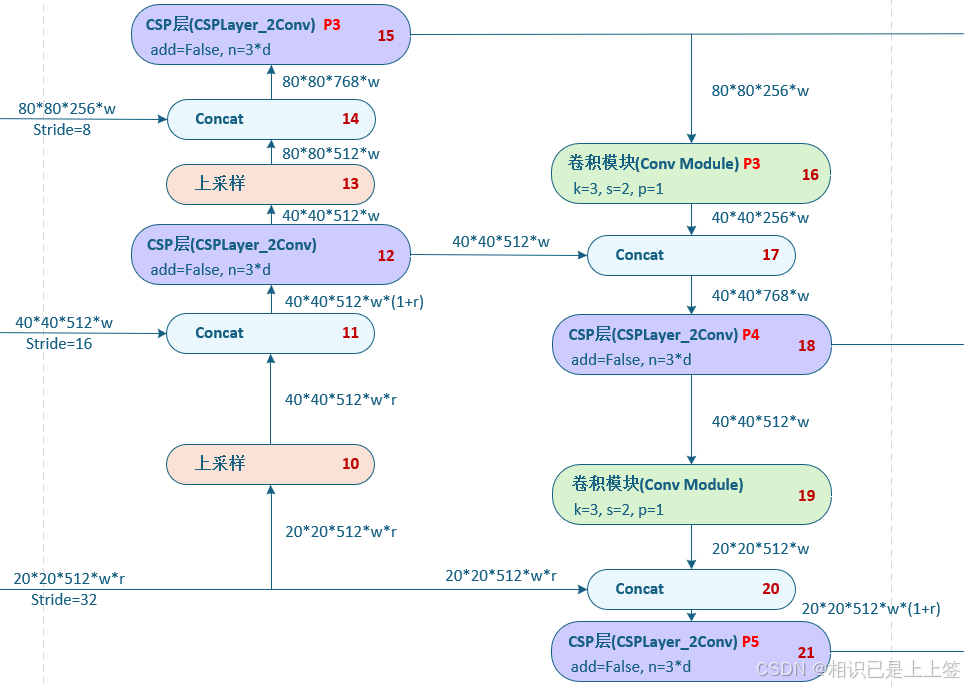
三、特征融合网络PAFPN

PAFPN是对经典特征金字塔FPN的优化和改进。

PAFPN网络里的CSP层参数add是等于False的，未引入残差连接，只进行简单的模块叠加，不需要更深层次的计算。

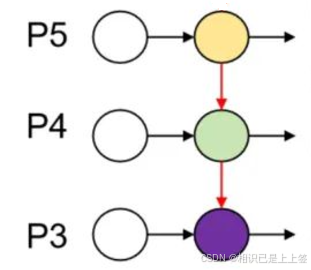
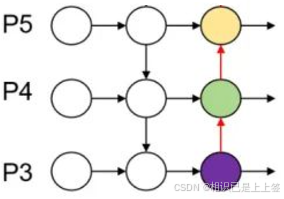
FPN通过建立从多尺度高级语义特征自顶向下的融合和侧向连接构建更高级的特征金字塔。目的是解决高层特征图分辨率低、细节信息少的问题。

PAFPN相对FPN又增加了一层自底向上的融合架构，以进一步提取全局语义信息，帮助网络更好地理解整个图像的语义结构。这样会更全面、准确地捕获不同尺度的物体，从而提升在视觉任务中性能。

四、Head

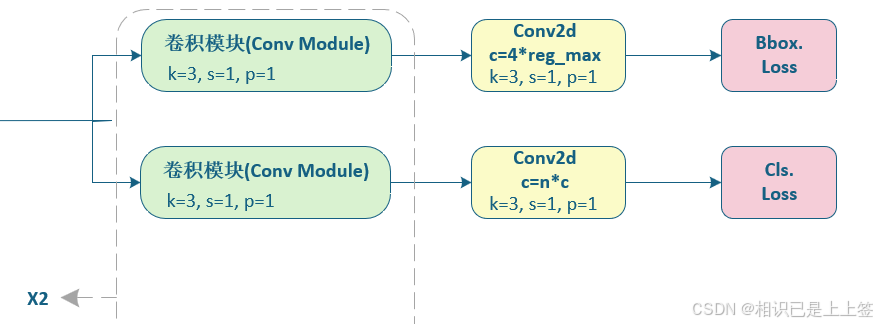
4.1 解耦合头

在目标检测任务中，传统的检测头通常会在同一个网络输出层共享一些特征进行分类和回归（如边界框回归）。然而，由于分类和回归是两个性质不同的任务，它们的目标和优化目标通常是不完全一致的。如果在同一头部进行预测，可能会导致梯度传递时出现干扰，从而影响任务的学习效果。为了避免这种问题，解耦合头提出了将不同任务的预测进行分开处理的策略。

详细的网络结构如下：

解耦合头通过将分类任务和回归任务分别交给不同的网络层来处理。分类任务使用一个独立的头进行类别概率预测，而回归任务则使用另一个独立的头进行边界框的预测。

解耦合头能够使得每个任务在优化过程中能够专注于各自的目标，从而提高各自的精度。对于边界框回归任务而言，解耦合可以使得回归预测更加精确；而分类任务也不再受回归预测的干扰，能够更加准确地进行分类。

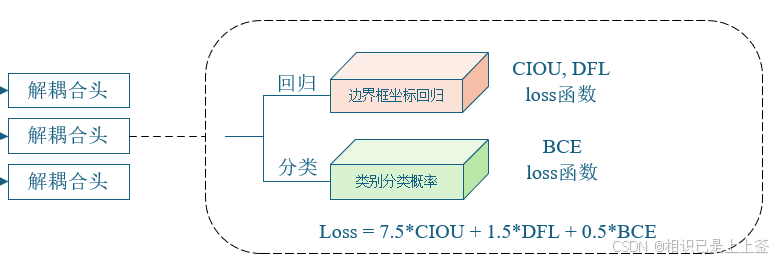
4.2 坐标回归Loss函数

坐标回归Loss函数由两个Loss函数组成，包含CIOU Loss和DFL loss，通过不同的权重相乘得到。

4.2.1 CIOU Loss

CIOU是由IOU、GIOU、 DIOU逐渐演变改进而来。

IOU：

$IoU=\frac{A\cap B}{B\cup B}$

A预测框，B真实框

缺点：若两个目标没有重叠，IoU将会为０, 并且不会反应两个目标之间的距离，在这种无重叠目标的情况下，如果IoU用作于损失函数，梯度为０，无法优化；IoU无法精确的反映两者的重合度大小。

GIOU：

$GIoU=IoU-\frac{C-(A\cup B)}{C}$

C是两个框的最小外接矩形的面积。

缺点：当两个框属于包含关系时，GIoU会退化成IoU，无法区分其相对位置关系；由于GIoU仍然严重依赖IoU，因此在两个垂直方向，误差很大，很难收敛。

DIOU：

$DIoU=IoU-\frac{\rho^{2}(b, b^{gt})}{c^{2}}$

ρ 代表的是计算预测框与真实框中心点间的欧式距离。

c 代表的是能够同时包含预测框和真实框的最小外接矩形的对角线长度。

缺点： DIOU虽然能够直接最小化预测框和真实框的中心点距离加速收敛，但是Bounding box的回归还有一个重要的因素纵横比暂未考虑。

CIOU：

$DIoU=IoU-(\frac{\rho^{2}(b, b^{gt})}{c^{2}}+\alpha \nu)$

α是权重函数。

$\alpha =\frac{\nu }{(1-IoU)+\nu }$

v用来度量宽高比的一致性。

$\nu =\frac{4}{\pi ^{2}}(\arctan \frac{w_{gt}}{h_{gt}}-\arctan \frac{w}{h})^{2}$

缺点：虽然考虑了框的纵横比，可以解决DIoU的问题。但是v反映的是纵横比的差异，而不是宽高分别与其置信度的真实差异，所以有时会阻碍模型有效的优化相似性。

所以后续出现各种改进EIOU，SIOU，WIOU等，详细介绍可以自行查询了解！

4.2.2 DFL Loss

其主要用于处理边界框回归任务，尤其是在分类模型中利用离散分布表示连续边界框回归的问题。该损失由 GFLv2 (Generalized Focal Loss v2) 提出，旨在增强模型的预测能力。

在yolov5中，回归边界框只使用CIOU有一些局限性，CIOU 是基于直接回归边界框的中心点和宽高参数，这种直接优化方式对预测精度有较高要求，可能会导致训练不稳定。CIOU 直接对连续边界框回归，缺乏对边界框预测分布的建模，无法充分挖掘回归任务中的分布特性。

DFL (Distribution Focal Loss) 是一种通过离散分布优化边界框预测的损失函数。

1. 可以将边界框参数（如中心点、宽、高）离散化为多个离散值，并预测其概率分布。通过分布建模，可以更细粒度地学习边界框信息。

2. 通过加权平均的方法，利用离散分布恢复连续值，增强预测的平滑性和稳定性。

3. DFL 将回归任务从单点预测转变为分布预测，使得模型能够更准确地拟合复杂的目标边界。

$DFL(S_{i}, S_{i+1})=-((y_{i+1}-y)log(S_{i})+(y-y_{i})log(S_{i+1}))$

其中

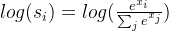
$log(s_{i})=log(\frac{e^{x_{i}}}{\sum _{j}e^{x_{j}}})$ ， $log(s_{i+1})=log(\frac{e^{x_{i+1}}}{\sum _{j}e^{x_{j}}})$

实际上S为softmax， $(y_{i+1}-y)$ 和 $(y-y_{i})$ 是其分别的权重，DFL可以说是交叉熵损失函数的一个连续形式

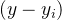
class DFLoss(nn.Module):
    """Criterion class for computing DFL losses during training."""

    def __init__(self, reg_max=16) -> None:
        """Initialize the DFL module."""
        super().__init__()
        self.reg_max = reg_max

    def __call__(self, pred_dist, target):
        """
        Return sum of left and right DFL losses.

        Distribution Focal Loss (DFL) proposed in Generalized Focal Loss
        https://ieeexplore.ieee.org/document/9792391
        """
        target = target.clamp_(0, self.reg_max - 1 - 0.01)
        tl = target.long()  # target left 这里对真实值取整，作为左侧的值
        tr = tl + 1  # target right 这里直接+1作为右侧的值
        wl = tr - target  # weight left 这里是左边的权重值
        wr = 1 - wl  # weight right 这里是右边的权重值
        return (
            F.cross_entropy(pred_dist, tl.view(-1), reduction="none").view(tl.shape) * wl
            + F.cross_entropy(pred_dist, tr.view(-1), reduction="none").view(tl.shape) * wr
        ).mean(-1, keepdim=True)

4.3 分类BCE Loss函数

对于经典的BCE Loss函数，通过单样本和批量样本来介绍。

4.3.1 单样本

在单样本中，假设真是标签为y 为二值变量取值为0和1，p为模型预测的概率。

$BCE(y, p)=-(ylog(p)+(1-y)log(1-p))$

当y=1时，表示真实发生，期望概率p值尽可能趋近于1，那么损失函数就会惩罚p值偏低的情况。

当y=0时，表示真实未发生，期望概率p值尽可能趋近于0，那么损失函数就会惩罚p值偏高的情况。

4.3.2 批量样本

在批量样本中，损失值就是求的平均损失值，即单个样本损失值相加总和除以样本数量。

$BCE=-\frac{1}{n}\sum_{i=1}^{n}(y_{i}log(p_{i})+(1-y_{i})log(1-p_{i}))$

五、结语

仅供学习使用！！！