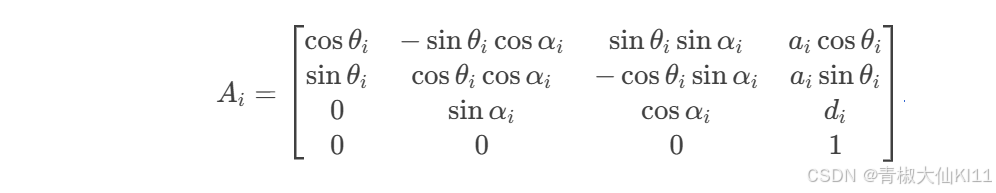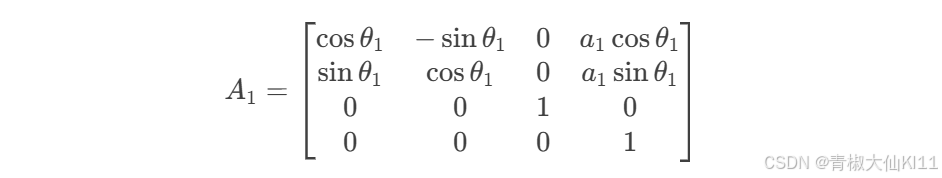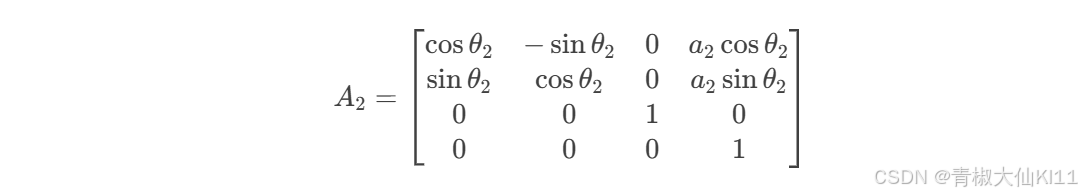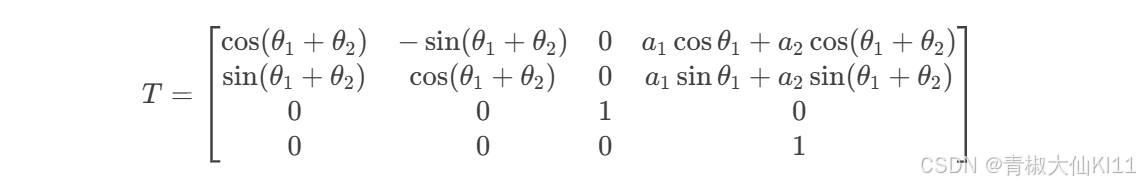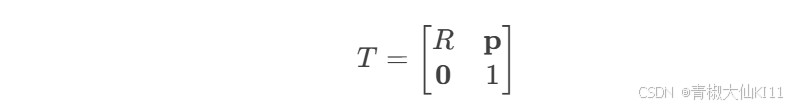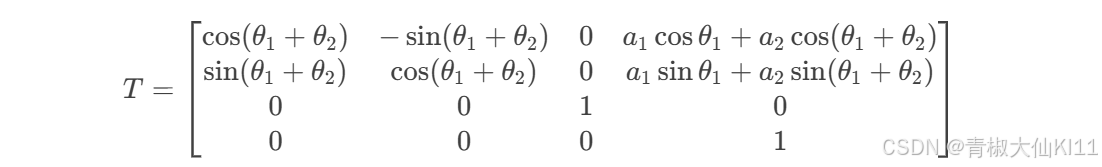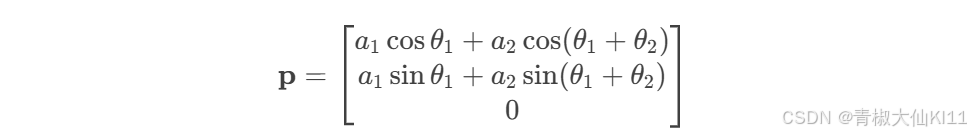变换矩阵
机器人通常包含多个关节和连杆,每个关节和连杆都有自己的局部坐标系。变换矩阵能够将一个点或向量从一个坐标系转换到另一个坐标系,从而实现对机器人各个部件位置和姿态的统一描述
变换矩阵能够将复杂的运动分解为旋转和平移的组合。通过矩阵乘法,可以将多个连续的运动操作合并为一个单一的变换矩阵,从而简化运动学分析。例如,在机器人正运动学中,通过连乘各个关节的变换矩阵,可以得到末端执行器的总变换矩阵。
在机器人学中,各连杆的变换矩阵用于描述相邻连杆坐标系之间的位置和姿态关系。通常使用Denavit-Hartenberg(D-H)参数法来求解变换矩阵。以下是一个简单的例子:
1. D-H 参数
D-H 参数包括四个参数:
-
a:连杆长度(沿 x 轴的距离)
-
α:连杆扭角(绕 x 轴的旋转角)
-
d:连杆偏距(沿 z 轴的距离)
-
θ:关节角度(绕 z 轴的旋转角)
2. 变换矩阵公式
相邻连杆的变换矩阵 Ai 可以表示为:
3. 示例
假设有一个简单的两连杆机械臂,D-H 参数如下
| 连杆 | ai | αi | di | θi |
|---|---|---|---|---|
| 1 | a1 | 0 | 0 | θ1 |
| 2 | a2 | 0 | 0 | θ2 |
连杆1的变换矩阵 A1
连杆2的变换矩阵 A2
总变换矩阵 T
总变换矩阵 T 是各连杆变换矩阵的乘积:
T=A1⋅A2
4. 计算总变换矩阵
将 A1 和 A2 相乘,得到:
总变换矩阵有什么用
总变换矩阵在机器人学、计算机图形学和控制系统中具有重要作用,主要用于描述机器人末端执行器(或任何目标点)相对于基坐标系的位置和姿态。以下是总变换矩阵的主要用途:
1. 描述位置和姿态
总变换矩阵 T 是一个 4x4 矩阵,包含旋转和平移信息:
-
R:3x3 旋转矩阵,描述末端执行器的姿态(方向)。
-
p:3x1 位置向量,描述末端执行器的位置。
-
0:1x3 零向量,用于齐次坐标的规范化。
通过总变换矩阵,可以清晰地知道机器人末端执行器在空间中的位置和方向。
2. 运动学分析
总变换矩阵是机器人正运动学分析的核心工具。通过将各连杆的变换矩阵相乘,可以得到末端执行器相对于基坐标系的位姿。这对于机器人路径规划、轨迹生成和运动控制至关重要。
3. 坐标变换
总变换矩阵可以将一个坐标系中的点或向量转换到另一个坐标系中。例如:
-
将末端执行器的坐标系中的点转换到基坐标系。
-
将传感器数据转换到机器人基坐标系。
4. 路径规划和轨迹生成
在机器人路径规划中,总变换矩阵用于计算机器人末端执行器的目标位置和姿态。通过逆运动学,可以进一步求解关节角度,使机器人达到目标位姿。
5. 碰撞检测
在机器人工作空间中,总变换矩阵可以用于检测机器人是否与环境中的障碍物发生碰撞。通过计算机器人各连杆的位置和姿态,可以判断其是否与障碍物相交。
6. 仿真和可视化
在机器人仿真和可视化中,总变换矩阵用于更新机器人模型的位置和姿态。通过实时计算总变换矩阵,可以在仿真环境中动态显示机器人的运动。
7. 控制系统
在机器人控制系统中,总变换矩阵用于反馈控制。通过传感器获取末端执行器的实际位姿,与目标位姿进行比较,可以生成控制信号,驱动机器人达到目标。
8. 多机器人协作
在多机器人系统中,总变换矩阵可以描述不同机器人之间的相对位置和姿态,从而实现协作任务。
示例
假设一个两连杆机械臂的总变换矩阵为:
-
位置:末端执行器的位置为:
-
姿态:末端执行器的姿态由旋转矩阵 R 描述。