二叉链表的先序建立、求二叉树的高度和叶子结点个数

二叉树（Binary Tree）是一种特殊的树形数据结构，特点是：每个结点至多只有两棵子树（即二叉树中不存在度大于2的结点），并且有左右子树之分，而且二叉树是有序树。

首先我们来熟悉一下二叉树的性质：

在二叉树的第i层上结点个数至多为 $2^{i-1}$ （i>=1）
深度为k的二叉树至多有 $2^k-1$ 个结点（k>=1）
具有n个结点的完全二叉树的深度为 $log_2 n] +1$
如果对一棵有n个结点的完全二叉树（深度为 $log_2 n] +1$ ）的结点按层次（从第一层到第 $log_2 n] +1$ 层，每层从左到右）编号，则对任一结点i(1<=i<=n），有
（1）如果i=1，则i是根，无双亲；如果i>1，则其双亲的编号是结点[i/2];
（2）如果2i>n，则结点i无左孩子，否则，即2i<=n，其左孩子的编号是2i；
（3）如果2i+1>n，则结点i无右孩子，否则，即2i+1<=n，其右孩子的编号是2i+1。
对任一棵二叉树，如果其终端结点数为n₀（即叶结点数为n₀），度为2的结点数为n₂，则n₀=n₂+1。

接下来我们就要进入正题了，用链式存储结构先序建立并且释放一棵二叉树。
首先我们要清楚，不是每个结点都有左右孩子的，因此我们需要在建树时使用虚结点（符号随意）来区分实际结点还是对应于空。其次，先序遍历的顺序是root->left->right。
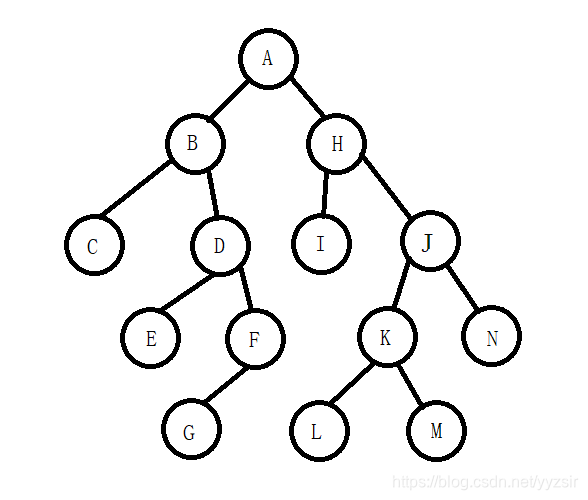
对于下图

扩充后的序列应为ABC##DE##FG###HI##JKL##M##N##，对于n个结点的二叉树，所要添加的虚结点个数为2n₀+n₁=n+1。
先序创建二叉树的二叉链表的构造函数如下：

template<class T>
BiTree<T>::BiTree()     
	{
		cout<<"请输入二叉树的结点数据:";     //使用#代表虚结点 
		this->root=Creat();
	}

递归创建二叉链表

template<class T>
BiNode<T>* BiTree<T>::Creat()     //先序建立二叉树的二叉链表 
{
	BiNode<T> *root;
	T ch;
	cin>>ch;
	if(ch=='#')root=NULL;
	else
	{
		root=new BiNode<T>;
		root->data=ch;
		root->lchild=Creat();   //创建左子树 
		root->rchild=Creat();   //创建右子树 
	}
	return root;
}

释放二叉链表

template <class T>
BiTree<T>::~BiTree()
{
    Release(root);
}
template <class T>
void BiTree<T>::Release(BiNode<T> *root)   //释放结点 
{
	if(root!=NULL)
	{
		Release(root->lchild);     //释放左子树
		Release(root->rchild);     //释放右子树
		delete root;      //释放当前根结点
	}
}

我们来对二叉树的二叉链表来进行一个应用——求二叉树的高度和叶子结点的个数

#include<iostream>
using namespace std;
//结点的数据可能是数字也可能是其他信息，所以使用类模版 
template<class T>
struct BiNode   //二叉树结点 
{
	T data;
	BiNode<T> *lchild,*rchild;   //指向左孩子和右孩子的指针 
};

template<class T>
class BiTree
{
	BiNode<T> *root; 
	BiNode<T> *Creat();
public:
	BiTree()     
	{
		cout<<"请输入二叉树的结点数据:";     //使用#代表虚结点 
		this->root=Creat();
	}
	void Release(BiNode<T> *root)   //释放结点 
	{
		if(root!=NULL)
		{
			Release(root->lchild);
			Release(root->rchild);
			delete root;
		}
	}	
	BiNode<T> *GetRoot()
	{
		return root;
	}
	~BiTree()
	{
		Release(root);
	}
	friend void CountLeaf(BiNode<T> *root,int &count);	
	friend int Height(BiNode<T> *root);
}; 

template<class T>
BiNode<T>* BiTree<T>::Creat()     //先序建立二叉树的二叉链表 
{
	BiNode<T> *root;
	T ch;
	cin>>ch;
	if(ch=='#')root=NULL;
	else
	{
		root=new BiNode<T>;
		root->data=ch;
		root->lchild=Creat();   //创建左子树 
		root->rchild=Creat();   //创建右子树 
	}
	return root;
}
template<class T>
void CountLeaf(BiNode<T> *root,int &count)     //求叶子结点的个数 
{
	if(root!=NULL)
	{
		if(root->lchild==NULL&&root->rchild==NULL)count++;   //当前root指向叶子 
		CountLeaf(root->lchild,count);
		CountLeaf(root->rchild,count);
	} 
}
template<class T>
int Height(BiNode<T> *root)      //求树的高度 
{
	int L,R;
	if(root==NULL)return 0;
	else
	{
		L=Height(root->lchild);
		R=Height(root->rchild);
		return (L>R)?L+1:R+1;
	}
}
int main()
{
	int count=0;
	BiTree<char> bt;  //创建一棵二叉树
	BiNode<char> *r=bt.GetRoot();
	CountLeaf(r,count);
	cout<<"叶节点数："<<count<<endl;
	cout<<"高度："<<Height(r); 
}

二叉链表的先序建立、求二叉树的高度和叶子结点个数

悦读