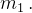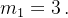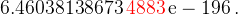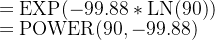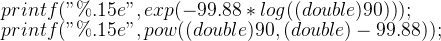摘要 用错数预测 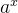
对于 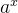

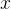
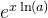
例1. 假设计算机利用 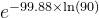
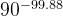
计算机首先计算 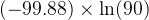
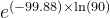
根据计算机的错误计算(二十七)知,前者即自变量的错误数字个数会影响到后者即函数值的结果的错误数字个数。具体有关系: 其中 等号左边的 2个变量依次表示函数值与自变量的错误数字个数,右边 3个变量依次代表导数、自变量以及函数值的扩展整数位数(扩展的意思是可以为任意整数)。
对于函数 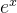
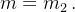
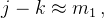
它意味着函数值的结果的错误数字个数约等于自变量的错误数字个数与自变量的整数位数的和。
下面给出计算机计算自变量 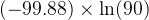
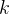
这样,上述蓝色与红色数字的组合为双精度下 16位的结果;而其整数位数为 3位,即
另外,由 ISReal 软件 可得 16位的正确结果是 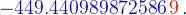

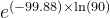
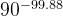
位错误数字。
例2. 在 Windows 10下,利用 Excel 2019MSO 以及 Visual Studio 2010 计算 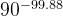
首先, 由 ISReal 软件 知,16位正确的近似值为
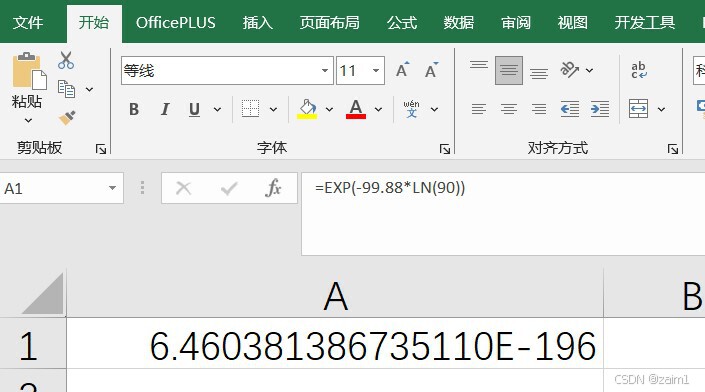
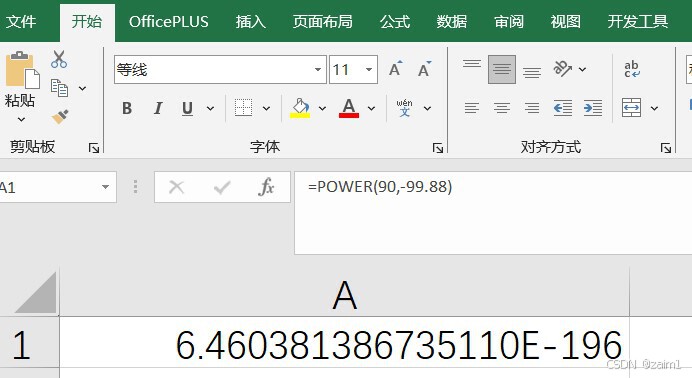
(1)在 Excel 的单元格中分别输入:
则输出的结果完全相同,并均有 4位错误数字。
下面是它们的贴图:
上面是第1张图.
上面是第2张图.
(2)在 Visual Studio 2010中运行下列两条语句
则输出分别为 6.460381386735107e-196 与 6.460381386735015e-196.
于是,两个结果同样均有 4位错误数字。