1 前言
内容为自己的学习总结,其中多有借鉴他人的地方,最后一并给出链接。
2 定义
在机器学习和谱图理论的学习中,总会用到正定矩阵半正定矩阵概念,了解它们的概念是十分必要的。
定义:正定矩阵(positive definite, PD)
给定一个大小为
n
×
n
n×n
n×n的实对称矩阵
A
A
A,若对于任意长度为
n
n
n的非零向量
X
X
X,有
X
T
A
X
>
0
X^TAX>0
XTAX>0恒成立,则矩阵
A
A
A是一个正定矩阵。
定义:半正定矩阵(positive semi-definite, PSD)
给定一个大小为
n
×
n
n×n
n×n的实对称矩阵
A
A
A,若对于任意长度为
n
n
n的非零向量
X
X
X,有
X
T
A
X
≥
0
X^TAX \ge 0
XTAX≥0恒成立,则矩阵
A
A
A是一个正定矩阵。
看个一个例子(来源参考文献【3】):
(1)单位矩阵
I
∈
R
2
×
2
I \in \mathbb{R}^{2 \times 2}
I∈R2×2是不是正定矩阵?
设向量
x
=
[
x
1
x
2
]
∈
R
2
\boldsymbol{x}=\left[\begin{array}{l} x_{1} \\ x_{2} \end{array}\right] \in \mathbb{R}^{2}
x=[x1x2]∈R2为非
0
0
0向量,则
x T I x = x T x = x 1 2 + x 2 2 \boldsymbol{x}^{T} I \boldsymbol{x}=\boldsymbol{x}^{T} \boldsymbol{x}=x_{1}^{2}+x_{2}^{2} xTIx=xTx=x12+x22
由于 x ≠ 0 \boldsymbol{x} \neq \mathbf{0} x=0,故而 x T I x > 0 \boldsymbol{x}^{T} I \boldsymbol{x}>0 xTIx>0恒成立,所以单位矩阵是正定矩阵。
从上面的例子看正定矩阵半正定矩阵和二次函数有些相似。以二次函数
y
=
a
x
2
y=ax^2
y=ax2为例 ,该函数的曲线会经过坐标原点,当参数
a
>
0
a>0
a>0时,曲线的“开口”向上,参数
a
<
0
a<0
a<0时,曲线的“开口”向下。
实际上可以把二次函数和
y
=
a
x
2
y=ax^2
y=ax2和
y
=
x
T
A
x
y=x^TAx
y=xTAx对比看。
- 在
y
=
a
x
2
y=ax^2
y=ax2中,若
a
>
0
a>0
a>0,则对于任意
x
≠
0
x\neq0
x=0,则有
y
>
0
y>0
y>0恒成立。
对应于 y = x T A x y=x^TAx y=xTAx,若 A A A为正定矩阵,则对于任意 x ≠ 0 x\neq0 x=0,则有 y > 0 y>0 y>0恒成立。 - 在
y
=
a
x
2
y=ax^2
y=ax2中,若
a
≥
0
a\geq0
a≥0,则对于任意
x
≠
0
x\neq0
x=0,则有
y
≥
0
y\geq0
y≥0恒成立。
对应于 y = x T A x y=x^TAx y=xTAx,若 A A A为半正定矩阵,则对于任意 x ≠ 0 x\neq0 x=0,则有 y ≥ 0 y\geq0 y≥0恒成立。
3 从几何的角度理解
若给定任意一个正定矩阵
A
∈
R
n
×
n
A\in R^{n\times n}
A∈Rn×n和一个非
0
0
0向量
x
∈
R
n
x\in R^n
x∈Rn,则两者相乘得到的向量
y
=
A
x
∈
R
n
y=Ax\in R^n
y=Ax∈Rn与向量
x
x
x的夹角恒小于
9
0
。
90^。
90。等价于
x
T
A
x
>
0
x^TAx>0
xTAx>0。
从矩阵的本质讲矩阵相乘实际上是向量
x
x
x安装矩阵
A
A
A指定的方式进行变换(矩阵的理解系列(一)(二)(三))。那么对于正定矩阵
x
T
A
x
=
x
T
M
>
0
x^TAx=x^TM>0
xTAx=xTM>0,记
M
=
A
x
M=Ax
M=Ax。有没有想起
C
o
s
Cos
Cos公式
cos
⟨
x
,
y
⟩
=
x
T
y
∥
x
∥
⋅
∥
y
∥
\cos \langle\boldsymbol{x}, \boldsymbol{y}\rangle=\frac{\boldsymbol{x}^{T} \boldsymbol{y}}{\|\boldsymbol{x}\| \cdot\|\boldsymbol{y}\|}
cos⟨x,y⟩=∥x∥⋅∥y∥xTy
到这里我们就可以理解正定矩阵的函数为:一个向量
x
x
x经过正定矩阵
A
A
A变换之后与原向量
x
x
x的夹角小于
9
0
。
90^。
90。。
再看个例子:给定向量
x
=
[
2
1
]
x=\left[\begin{array}{l}2 \\1\end{array}\right]
x=[21],对于单位矩阵
I
=
[
1
0
0
1
]
I=\left[\begin{array}{ll}1 & 0 \\0 & 1\end{array}\right]
I=[1001],则
y
=
I
x
=
x
=
[
2
1
]
\boldsymbol{y}=I \boldsymbol{x}=\boldsymbol{x}=\left[\begin{array}{l} 2 \\1\end{array}\right]
y=Ix=x=[21]则向量
y
和
x
y和x
y和x的夹角为0。
cos ⟨ x , y ⟩ = x T y ∥ x ∥ ⋅ ∥ y ∥ = 2 × 2 + 1 × 1 2 2 + 1 2 ⋅ 2 2 + 1 2 = 1 \begin{array}{l} \cos \langle\boldsymbol{x}, \boldsymbol{y}\rangle=\frac{\boldsymbol{x}^{T} \boldsymbol{y}}{\|\boldsymbol{x}\| \cdot\|\boldsymbol{y}\|} \\[6mm] =\frac{2 \times 2+1 \times 1}{\sqrt{2^{2}+1^{2}} \cdot \sqrt{2^{2}+1^{2}}} \\[6mm] =1 \end{array} cos⟨x,y⟩=∥x∥⋅∥y∥xTy=22+12⋅22+122×2+1×1=1
结合上面的例子和矩阵的运动我们可以理解正定矩阵:
- 对于一个向量 x x x,我们希望 x x x在经过有一个矩阵 A A A的变化后得到的新的向量 M M M和它本身的夹角小于 90 90 90度。
- 而小于 90 90 90度背后的含义是变换后的向量 M M M是沿着原向量 x x x的正方向进行缩放的(即 M M M投影回原向量时方向不变)
那么如何理解要求正定矩阵的特征值大于0?
首先一个矩阵
A
A
A的特征向量
x
x
x就是表示某个向量会沿着特征向量的方向进行变换(缩放),缩放比例由特征值
λ
\lambda
λ决定。(特征值和特征向量的理解)。举个例子【参考文献【1】】:
A
1
=
[
[
0.5
,
0
]
T
,
[
0
,
2
]
T
]
A_1=[[0.5, 0]^T,[0, 2]^T]
A1=[[0.5,0]T,[0,2]T]很简单地可以计算得到A的特征值分别是
0.5
0.5
0.5和
2
2
2,而它们对应的特征向量分别是
[
1
,
0
]
T
[1,0]^T
[1,0]T和
[
0
,
1
]
T
[0,1]^T
[0,1]T 。所以如果一个向量
b
b
b左乘一个矩阵
A
A
A,其本质就是将向量
b
b
b沿着
[
1
,
0
]
T
[1,0]^T
[1,0]T和
[
0
,
1
]
T
[0,1]^T
[0,1]T方向分别放大
0.5
0.5
0.5和
2
2
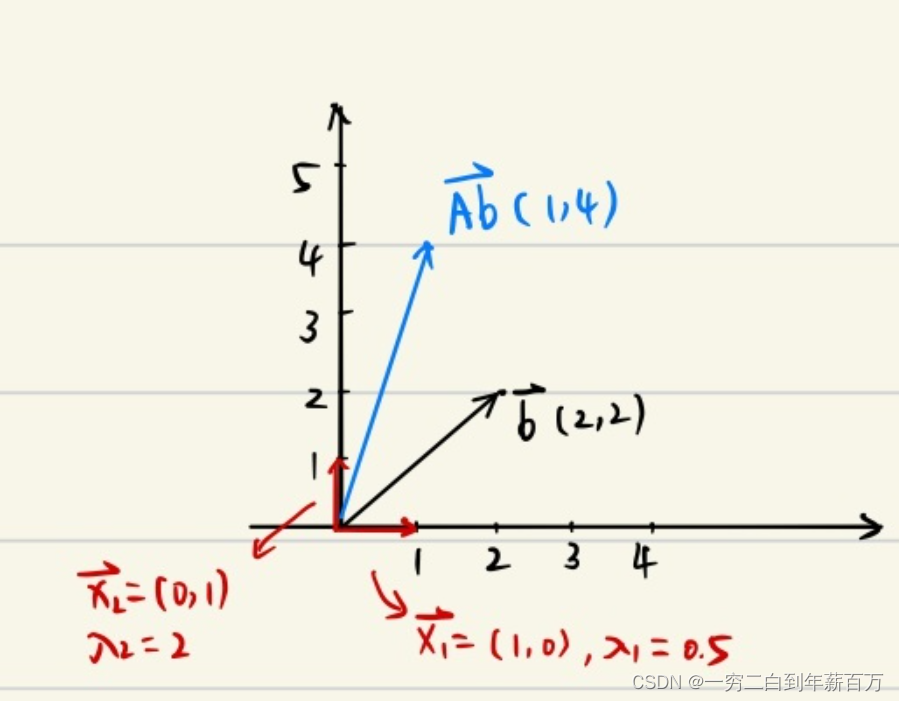
2倍。我们假设
b
=
[
2
,
2
]
T
b=[2,2]^T
b=[2,2]T,那么
A
b
Ab
Ab最终得到的向量为
[
1
,
4
]
T
[1, 4]^T
[1,4]T,结合下图看更加直观:
图片来着参考文献【1】
我们看上图,如果其中一个特征值小于
0
0
0,比如
λ
1
<
0
\lambda_1<0
λ1<0那么最终得到的向量
A
b
Ab
Ab投射到方向的向量与
b
b
b反向。综上,要使得变换后的向量
M
M
M与原向量
x
x
x夹角小于
90
90
90度,即映射回原来的向量时保持方向不变,那么就需要特征值大于
0
0
0,所以这也是为什么正定矩阵的特征值都大于
0
0
0.
A
x
=
λ
x
→
x
T
A
x
=
λ
x
T
x
=
λ
∥
x
∥
2
>
0
\begin{array}{c} A x=\lambda x \\ \rightarrow x^{T} A x=\lambda x^{T} x=\lambda\|x\|^{2}>0 \end{array}
Ax=λx→xTAx=λxTx=λ∥x∥2>0
故λ必须大于0,即特征值必须大于0。
正定矩阵跟优化的关系用到了在补充。
4 参考文献
[1]如何理解正定矩阵和半正定矩阵
[2]MIT线性代数笔记3.3(正定矩阵,最小值)
[3]浅谈「正定矩阵」和「半正定矩阵」
[4]MIT线性代数笔记3.1(对称矩阵,正定矩阵