注意力机制学习

学习于博客https://blog.csdn.net/weixin_44791964/article/details/121371986

1.Channel Attention

1.1 SeNet

对于输入进来的特征层，关注其每一个通道的权重，让网络关注它最需要关注的通道。【channel不变，h,w变】

代表性Senet具体实现方式是：
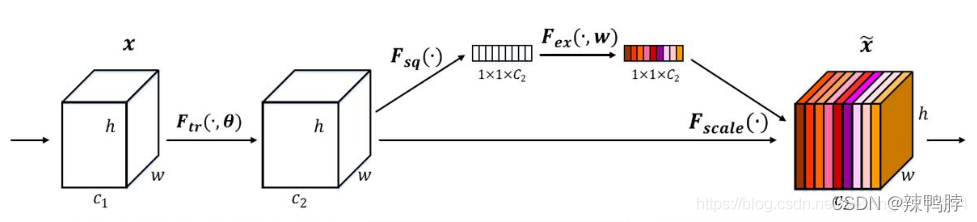
1、第一个操作：Squeeze（ $F_{sq}$ ），对输入进来的特征层进行全局池化（global pooling）,将每个通道的二维特征（h*w）压缩为1个实数，论文是通过平均值池化的方式实现。这属于空间维度的一种特征压缩，因为这个实数是根据二维特征所有值算出来的，所以在某种程度上具有全局的感受野，通道数保持不变，所以通过squeeze操作后变为1x1xC。
$z_c = F_{se}(u_c) = \frac{1}{H \times W} \displaystyle\sum_{i=1}^{H}\displaystyle\sum_{j=1}^{W}u_c(i,j)$
2、第二个操作：excitation( $F_{ex}$ )，通过参数来为每个特征通道生成一个权重值，权重值如何生成非常关键。文章中是通过两个全连接层组成一个Bootleneck结构去建模通道间的相关性，并输出和输入特征同样数目的权重值。具体来说，进行两次全连接，第一次全连接神经元个数较少，第二次全连接神经元个数和输入特征层相同。在完成两次全连接后，我们再取一次Sigmoid将值固定到0-1之间，此时我们获得了输入特征层每一个通道的权值（0-1之间）。
3、第三个操作：Scale（ $F_{scale}$ ）在获得这个权值后，我们将这个权值乘上原输入特征层即可。彩色图片就表示每个通道都有个权重。

论文认为在excitation操作中，用两个全连接层比直接用在一个全连接层的好处在于：1）具有更多的非线性；2）可以更好的拟合通道间复杂的关系。这里我们使用 global average pooling 作为 Squeeze 操作。紧接着两个 Fully Connected 层组成一个 Bottleneck 结构去建模通道间的相关性，并输出和输入特征同样数目的权重。我们首先将特征维度降低到输入的 1/16，然后经过 ReLu 激活后再通过一个 Fully Connected 层升回到原来的维度。这样做比直接用一个 Fully Connected 层的好处在于：1）具有更多的非线性，可以更好地拟合通道间复杂的相关性；2）极大地减少了参数量和计算量。然后通过一个 Sigmoid 的门获得 0~1 之间归一化的权重，最后通过一个 Scale 的操作来将归一化后的权重加权到每个通道的特征上。

启发：使用全连接网络，可以获得输入中每个值之间的关系。文章中未获得通道间的关系，先将每个通道中的特征用一个值表征，再使用全连接网络学习通道与通道间的关系。这个关系最后使用sigmoid输出，就是它们的权重。
来源于博客 Bubbliiiing
实现代码如下：

import torch
from torch import nn

class Senet(nn.Module):
    def __init__(self, channel, ratio=16):
        super(Senet, self).__init__()
        self.avg_pool = nn.AdaptiveAvgPool2d(1)  # 因为是关注channel，这里将h和w压为1
        self.fc = nn.Sequential(
            nn.Linear(channel, channel//ratio, False),
            nn.ReLU(),
            nn.Linear(channel//ratio, channel, False),
            nn.Sigmoid(),
        )

    def forward(self,x):
        b, c, h, w = x.size()
        avg = self.avg_pool(x).view([b,c])  # 将压为1的h,w view
        fc  = self.fc(avg).view([b,c,1,1])  # 这里计算每一个channel 的w后，变回与input一样的size，便于点积
        return x*fc

model = Senet(512)
print(model)
input = torch.ones([2,512,26,26])
print(input)
output = model(input)
print(output)

1.2 ECANet

ECANet是也是通道注意力机制的一种实现形式。ECANet可以看作是SENet的改进版。
ECANet的作者认为SENet对通道注意力机制的预测带来了副作用，捕获所有通道的依赖关系是低效并且是不必要的。
在ECANet的论文中，作者认为卷积具有良好的跨通道信息获取能力。

ECA模块的思想是非常简单的，它去除了原来SE模块中的全连接层，直接在全局平均池化之后的特征上通过一个1D卷积进行学习。

既然使用到了1D卷积，那么1D卷积的卷积核大小的选择就变得非常重要了，了解过卷积原理的同学很快就可以明白，1D卷积的卷积核大小会影响注意力机制每个权重的计算要考虑的通道数量。用更专业的名词就是跨通道交互的覆盖率。

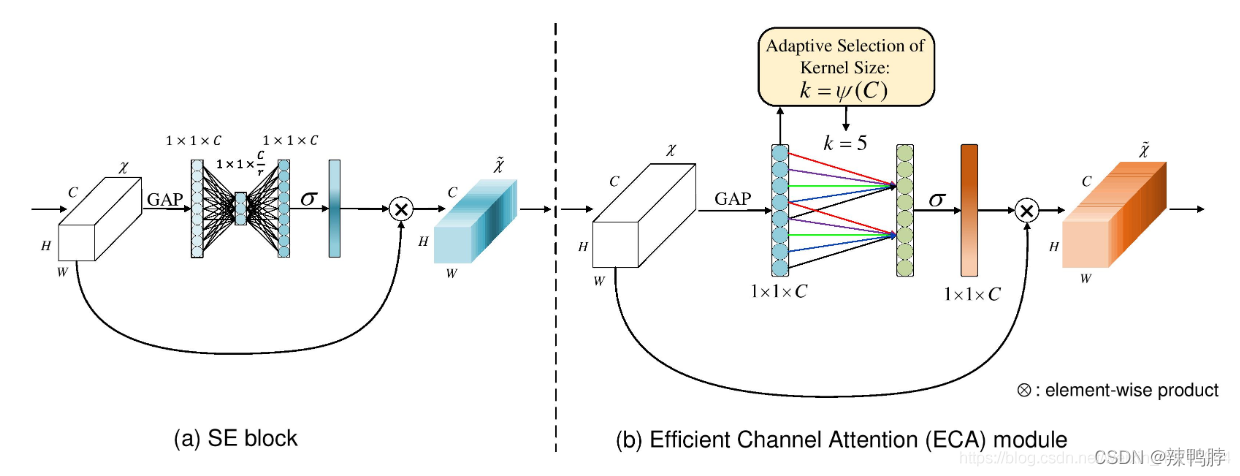
如下图所示，左图是常规的SE模块，右图是ECA模块。ECA模块用1D卷积替换两次全连接。

来源于博客 Bubbliiiing

2.Spatial Attention

空间注意力机制，更关注于每一个像素点的权重。因此会对每一个像素点的所有channel取最大值和平均值。之后将这两个feature map进行一个堆叠，利用一次通道数为1的卷积调整通道数为1，然后取一个sigmoid，此时我们获得了输入特征层每一个特征点的权值（0-1之间）。在获得这个权值后，我们将这个权值乘上原输入特征层即可。【h,w不变，chaneel变】

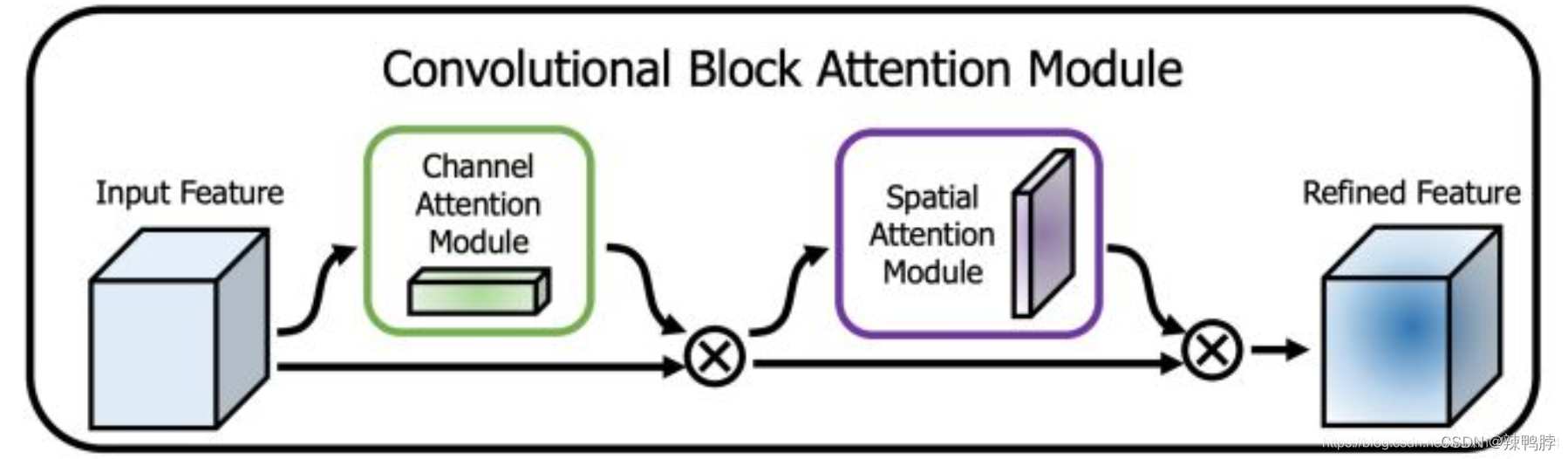
代表性CBAM实现方式，将通道注意力机制和空间注意力机制进行结合，实现示意图如下所示，CBAM会对输入进来的特征层，分别进行通道注意力机制的处理和空间注意力机制的处理。
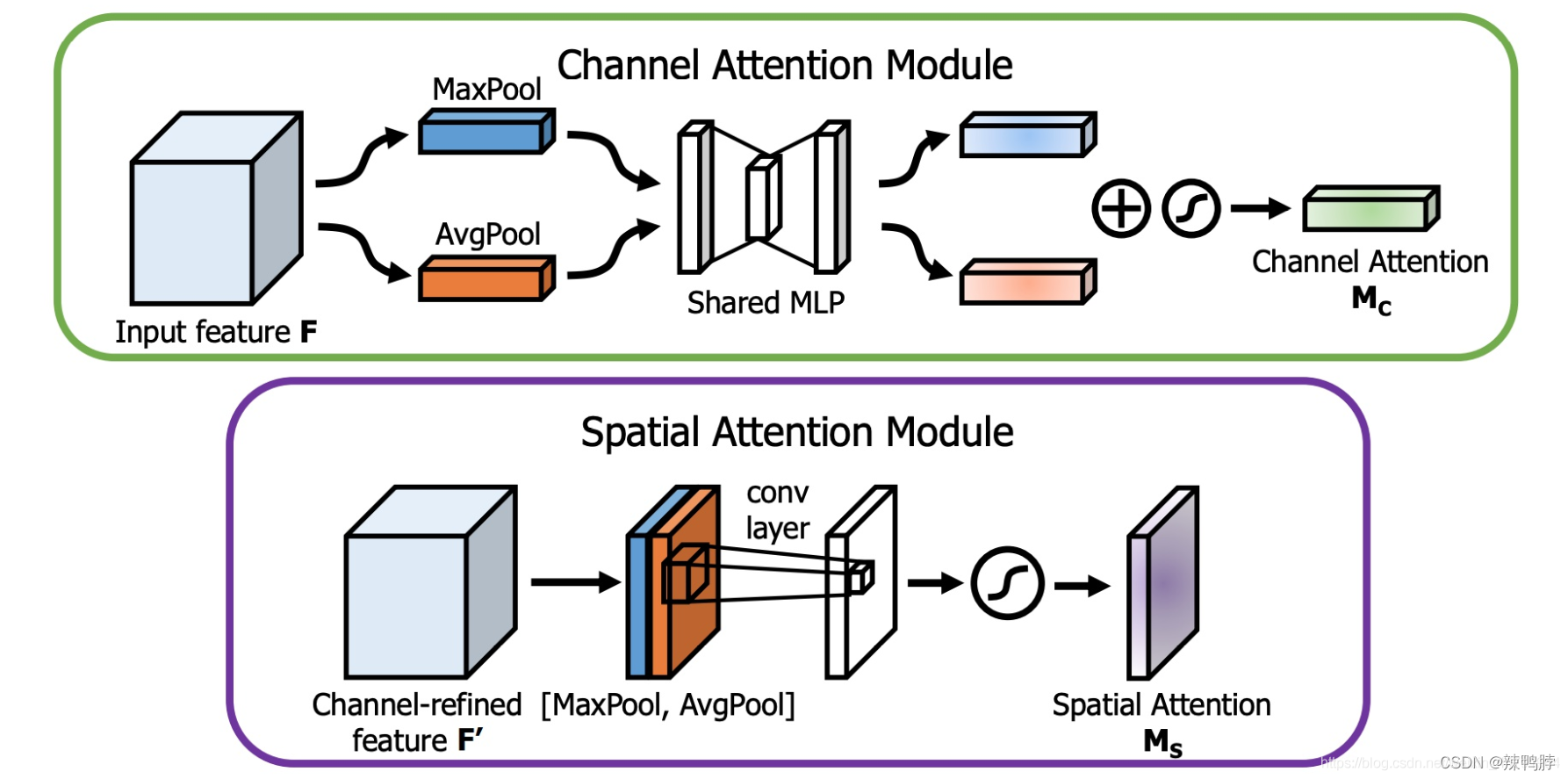
来源于博客 Bubbliiiing
下图是通道注意力机制和空间注意力机制的具体实现方式：
图像的上半部分为通道注意力机制，通道注意力机制的实现可以分为两个部分，我们会对输入进来的单个特征层，分别进行全局平均池化和全局最大池化。之后对平均池化和最大池化的结果，利用共享的全连接层进行处理，我们会对处理后的两个结果进行相加，然后取一个sigmoid，此时我们获得了输入特征层每一个通道的权值（0-1之间）。在获得这个权值后，我们将这个权值乘上原输入特征层即可。

图像的下半部分为空间注意力机制，我们会对输入进来的特征层，在每一个特征点的通道上取最大值和平均值。之后将这两个结果进行一个堆叠，利用一次通道数为1的卷积调整通道数，然后取一个sigmoid，此时我们获得了输入特征层每一个特征点的权值（0-1之间）。在获得这个权值后，我们将这个权值乘上原输入特征层即可。

来源于博客 Bubbliiiing

from turtle import forward
import torch
from torch import nn
# channel注意力机制
class ChannelAttention(nn.Module):
    def __init__(self,channel,ratio=16):
        super(ChannelAttention,self).__init__()
        self.max_pool = nn.AdaptiveMaxPool2d(1)  # 全局最大池化
        self.avg_pool = nn.AdaptiveAvgPool2d(1)

        self.fc = nn.Sequential(
            nn.Linear(channel, channel//ratio,False),
            nn.ReLU(),
            nn.Linear(channel//ratio,channel,False),
        )

        self.sigmoid = nn.Sigmoid()
        # 以上为网络的定义部分

    def forward(self,x):    #前向传播，把网络串起来
        b,c,h,w =  x.size()
        out_max_pool =  self.max_pool(x).view([b,c])
        out_avg_pool =  self.avg_pool(x).view([b,c])
        out_fc_max =self.fc(out_max_pool)
        out_fc_avg =self.fc(out_avg_pool)
        out = out_fc_avg + out_fc_max
        out = self.sigmoid(out).view([b,c,1,1])
        return out*x
        
# spatial注意力机制      
class SpatialAttention(nn.Module):
    def __init__(self,kernel_size = 7):
        super(SpatialAttention,self).__init__()
        padding = 7//2
        self.conv1 = nn.Conv2d(2,1,kernel_size,1, padding, bias=False)
        self.sigmoid = nn.Sigmoid()

    def forward(self,x):
        out_avg = torch.mean(x, dim=1, keepdim=True)
        out_max,_ = torch.max(x, dim=1, keepdim=True)
        out_pool = torch.cat([out_max,out_avg],dim=1)
        out = self.conv1(out_pool)
        out = self.sigmoid(out)

        return out*x

class CBAM(nn.Module):
    def __init__(self, channel, ratio=16, kernel_size=7):
        super(CBAM,self).__init__()
        # 定义部分
        self.channel_attention = ChannelAttention(channel,ratio)
        self.spatial_attention = SpatialAttention(kernel_size)
    def forward(self, x):
        out_channel_attention = self.channel_attention(x)
        out_spatial_attention = self.spatial_attention(out_channel_attention)
        return out_spatial_attention

model = CBAM(512)
print(model)
input = torch.ones([2,512,26,26])
# print(input)
output = model(input)
print(output)

3 应用

注意力机制是一个即插即用的模块，建议不要在主干网络插入。注意力机制的使用，输入时只需要关注channel数。
注意力机制是一个即插即用的模块，理论上可以放在任何一个特征层后面，可以放在主干网络，也可以放在加强特征提取网络。

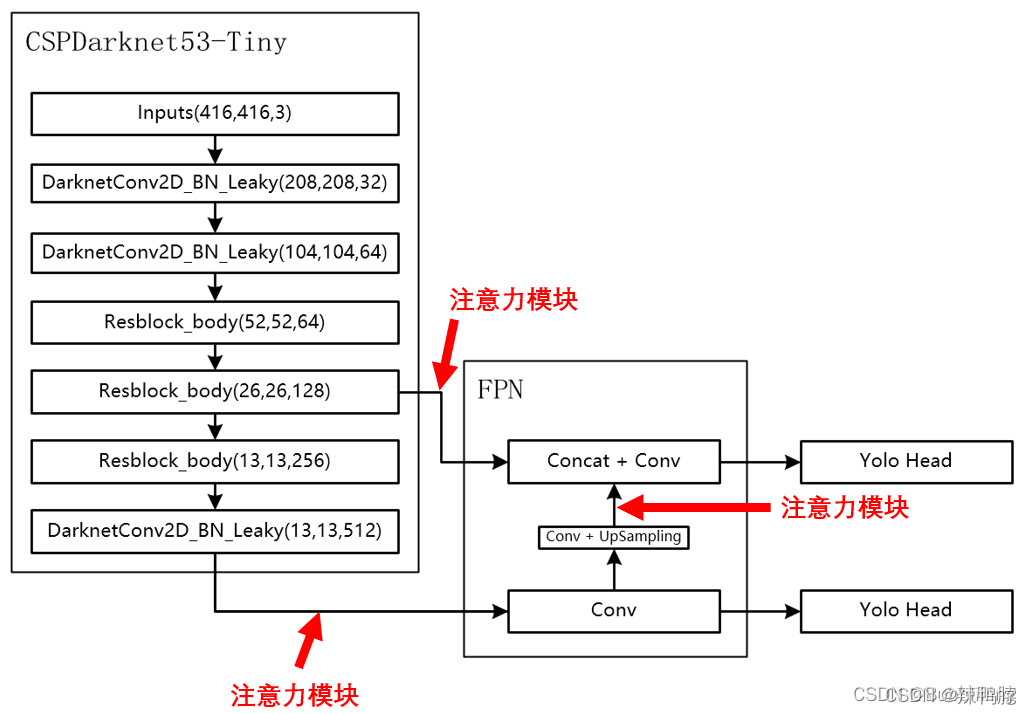
由于放置在主干会导致网络的预训练权重无法使用，本文以YoloV4-tiny为例，将注意力机制应用加强特征提取网络上。

如下图所示，我们在主干网络提取出来的两个有效特征层上增加了注意力机制，同时对上采样后的结果增加了注意力机制。
来源于博客 Bubbliiiing

attention_block = [se_block, cbam_block, eca_block]

#---------------------------------------------------#
#   特征层->最后的输出
#---------------------------------------------------#
class YoloBody(nn.Module):
    def __init__(self, anchors_mask, num_classes, phi=0):
        super(YoloBody, self).__init__()
        self.phi            = phi
        self.backbone       = darknet53_tiny(None)

        self.conv_for_P5    = BasicConv(512,256,1)
        self.yolo_headP5    = yolo_head([512, len(anchors_mask[0]) * (5 + num_classes)],256)

        self.upsample       = Upsample(256,128)
        self.yolo_headP4    = yolo_head([256, len(anchors_mask[1]) * (5 + num_classes)],384)

        if 1 <= self.phi and self.phi <= 3:
            self.feat1_att      = attention_block[self.phi - 1](256)
            self.feat2_att      = attention_block[self.phi - 1](512)
            self.upsample_att   = attention_block[self.phi - 1](128)

    def forward(self, x):
        #---------------------------------------------------#
        #   生成CSPdarknet53_tiny的主干模型
        #   feat1的shape为26,26,256
        #   feat2的shape为13,13,512
        #---------------------------------------------------#
        feat1, feat2 = self.backbone(x)
        if 1 <= self.phi and self.phi <= 3:
            feat1 = self.feat1_att(feat1)
            feat2 = self.feat2_att(feat2)

        # 13,13,512 -> 13,13,256
        P5 = self.conv_for_P5(feat2)
        # 13,13,256 -> 13,13,512 -> 13,13,255
        out0 = self.yolo_headP5(P5) 

        # 13,13,256 -> 13,13,128 -> 26,26,128
        P5_Upsample = self.upsample(P5)
        # 26,26,256 + 26,26,128 -> 26,26,384
        if 1 <= self.phi and self.phi <= 3:
            P5_Upsample = self.upsample_att(P5_Upsample)
        P4 = torch.cat([P5_Upsample,feat1],axis=1)

        # 26,26,384 -> 26,26,256 -> 26,26,255
        out1 = self.yolo_headP4(P4)
        
        return out0, out1

Attention模块

import torch
import torch.nn as nn
import math

class se_block(nn.Module):
    def __init__(self, channel, ratio=16):
        super(se_block, self).__init__()
        self.avg_pool = nn.AdaptiveAvgPool2d(1)
        self.fc = nn.Sequential(
                nn.Linear(channel, channel // ratio, bias=False),
                nn.ReLU(inplace=True),
                nn.Linear(channel // ratio, channel, bias=False),
                nn.Sigmoid()
        )

    def forward(self, x):
        b, c, _, _ = x.size()
        y = self.avg_pool(x).view(b, c)
        y = self.fc(y).view(b, c, 1, 1)
        return x * y

class ChannelAttention(nn.Module):
    def __init__(self, in_planes, ratio=8):
        super(ChannelAttention, self).__init__()
        self.avg_pool = nn.AdaptiveAvgPool2d(1)
        self.max_pool = nn.AdaptiveMaxPool2d(1)

        # 利用1x1卷积代替全连接
        self.fc1   = nn.Conv2d(in_planes, in_planes // ratio, 1, bias=False)
        self.relu1 = nn.ReLU()
        self.fc2   = nn.Conv2d(in_planes // ratio, in_planes, 1, bias=False)

        self.sigmoid = nn.Sigmoid()

    def forward(self, x):
        avg_out = self.fc2(self.relu1(self.fc1(self.avg_pool(x))))
        max_out = self.fc2(self.relu1(self.fc1(self.max_pool(x))))
        out = avg_out + max_out
        return self.sigmoid(out)

class SpatialAttention(nn.Module):
    def __init__(self, kernel_size=7):
        super(SpatialAttention, self).__init__()

        assert kernel_size in (3, 7), 'kernel size must be 3 or 7'
        padding = 3 if kernel_size == 7 else 1
        self.conv1 = nn.Conv2d(2, 1, kernel_size, padding=padding, bias=False)
        self.sigmoid = nn.Sigmoid()

    def forward(self, x):
        avg_out = torch.mean(x, dim=1, keepdim=True)
        max_out, _ = torch.max(x, dim=1, keepdim=True)
        x = torch.cat([avg_out, max_out], dim=1)
        x = self.conv1(x)
        return self.sigmoid(x)

class cbam_block(nn.Module):
    def __init__(self, channel, ratio=8, kernel_size=7):
        super(cbam_block, self).__init__()
        self.channelattention = ChannelAttention(channel, ratio=ratio)
        self.spatialattention = SpatialAttention(kernel_size=kernel_size)

    def forward(self, x):
        x = x * self.channelattention(x)
        x = x * self.spatialattention(x)
        return x

class eca_block(nn.Module):
    def __init__(self, channel, b=1, gamma=2):
        super(eca_block, self).__init__()
        kernel_size = int(abs((math.log(channel, 2) + b) / gamma))
        kernel_size = kernel_size if kernel_size % 2 else kernel_size + 1
        
        self.avg_pool = nn.AdaptiveAvgPool2d(1)
        self.conv = nn.Conv1d(1, 1, kernel_size=kernel_size, padding=(kernel_size - 1) // 2, bias=False) 
        self.sigmoid = nn.Sigmoid()

    def forward(self, x):
        y = self.avg_pool(x)
        y = self.conv(y.squeeze(-1).transpose(-1, -2)).transpose(-1, -2).unsqueeze(-1)
        y = self.sigmoid(y)
        return x * y.expand_as(x)

4.Self-Attention

Self-attention是Transformer最核心的思想，关键就是Q、K、V三个矩阵以及背后的核心意义。

1. 基础知识：

向量的内积是什么，几何意义
答：向量的内积表征两个向量的夹角，表征一个向量在另一个向量上的投影，投影值越高，两个向量相关度越高。
矩阵与自身的转置相乘，得到的结果的意义
答：矩阵可以看作由一些向量组成，一个矩阵乘以它自己转置的运算，其实可以看成这些向量分别与其他向量计算内积。（此时脑海里想起矩阵乘法的口诀，第一行乘以第一列、第一行乘以第二列…嗯哼，矩阵转置以后第一行不就是第一列吗？这是在计算第一个行向量与自己的内积，第一行乘以第二列是计算第一个行向量与第二个行向量的内积第一行乘以第三列是计算第一个行向量与第三个行向量的内积…）
矩阵与自身转置点积，就是计算矩阵中的每一行向量，与自身和其他行向量的相关度。

更多请参考 http://t.csdn.cn/avbja

意义

self-attention可以视为一个特征提取层，给定输入特征 ${a^1,a^2,\cdots,a^n}$ ,经过self-attention layer，融合每个输入特征，得到新的特征 ${b^1,b^2,\cdots,b^n}$ 。

from math import sqrt
 
import torch
import torch.nn as nn
 
class SelfAttention(nn.Module):
    def __init__(self, dim_q, dim_k, dim_v):
        super(SelfAttention, self).__init__()
        self.dim_q = dim_q
        self.dim_k = dim_k
        self.dim_v = dim_v
 
        #定义线性变换函数
        self.linear_q = nn.Linear(dim_q, dim_k, bias=False)
        self.linear_k = nn.Linear(dim_q, dim_k, bias=False)
        self.linear_v = nn.Linear(dim_q, dim_v, bias=False)
        self._norm_fact = 1 / sqrt(dim_k)
 
    def forward(self, x):
        # x: batch, n, dim_q
        #根据文本获得相应的维度
 
        batch, n, dim_q = x.shape
        assert dim_q == self.dim_q
 
        q = self.linear_q(x)  # batch, n, dim_k
        k = self.linear_k(x)  # batch, n, dim_k
        v = self.linear_v(x)  # batch, n, dim_v
        #q*k的转置 并*开根号后的dk
        dist = torch.bmm(q, k.transpose(1, 2)) * self._norm_fact  # batch, n, n
        #归一化获得attention的相关系数
        dist = torch.softmax(dist, dim=-1)  # batch, n, n
        #attention系数和v相乘，获得最终的得分
        att = torch.bmm(dist, v)
        return att