回溯

9. 分割回文串

131. 分割回文串

思路：
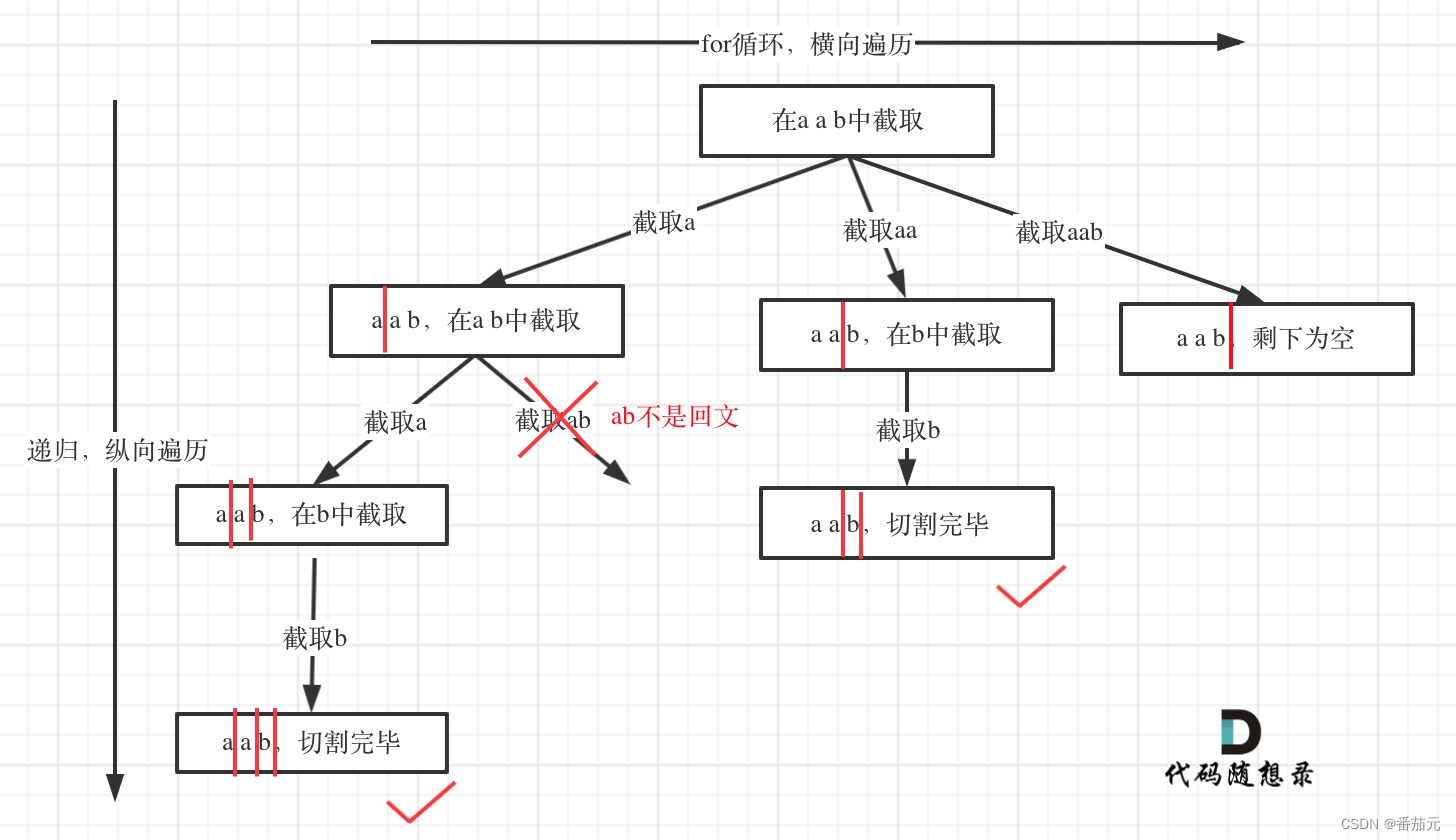
回溯法，分割思路如下：
选出长度逐渐增加的第一个回文子串，剩下的子串递归分割。

class Solution {
public:
    vector<vector<string>> partition(string s) {
        result.clear();
        path.clear();
        backtracking(s, 0);
        return result;
    }

private:
    vector<vector<string>> result;
    vector<string> path;
    void backtracking(const string &s, int startIndex) {
        // 如果 startIndex > s.size() 说明找到了一组答案
        if (startIndex >= s.size()) {
            result.push_back(path);
            return ;
        }

        for (int i = startIndex; i < s.size(); i++) {
            if (isPalindrome(s, startIndex, i)) {
                string str = s.substr(startIndex, i - startIndex + 1);
                path.push_back(str);
            } else {
                continue;
            }
            backtracking(s, i + 1);
            path.pop_back();
        }
    }

    bool isPalindrome(const string &s, int start, int end) {
        for (int i = start, j = end; i < j; i++, j--) {
            if (s[i] != s[j]) return false;
        }
        return true;
    }
};

优化：
上面的方法，会有很多的重复的回文串判断，并且所有的子串都至少被判断一次。因此，可以选择直接将所有的子串提前处理出来存储在数组中，然后直接查表判断某个子串是否是回文串，更省时间。

class Solution {
public:
    vector<vector<string>> partition(string s) {
        result.clear();
        path.clear();
        computePalindrome(s);
        backtracking(s, 0);
        return result;
    }

private:
    vector<vector<string>> result;
    vector<string> path;
    vector<vector<bool>> isPalindrome;
    void backtracking(const string &s, int startIndex) {
        // 如果 startIndex > s.size() 说明找到了一组答案
        if (startIndex >= s.size()) {
            result.push_back(path);
            return ;
        }

        for (int i = startIndex; i < s.size(); i++) {
            if (isPalindrome[startIndex][i]) {
                string str = s.substr(startIndex, i - startIndex + 1);
                path.push_back(str);
            } else {
                continue;
            }
            backtracking(s, i + 1);
            path.pop_back();
        }
    }

    // bool isPalindrome(const string &s, int start, int end) {
    //     for (int i = start, j = end; i < j; i++, j--) {
    //         if (s[i] != s[j]) return false;
    //     }
    //     return true;
    // }

    void computePalindrome(const string &s) {
        isPalindrome.resize(s.size(), vector<bool>(s.size(), false));
        for (int i = s.size() - 1; i >= 0; i--) {
            for (int j = i; j < s.size(); j++) {
                if (j == i) isPalindrome[i][j] = true;
                else if (j - i == 1) isPalindrome[i][j] = (s[i] == s[j]);
                else isPalindrome[i][j] = (s[i] == s[j] && isPalindrome[i+1][j-1]);
            }
        }
    }
};