数值分析第九章节用Python实现常微分方程初值问题的数值解法(Matlab补充版)

参考书籍：数值分析第五版李庆杨王能超易大义编第9章常微分方程初值问题的数值解法
文章声明：如有发现错误，欢迎批评指正

文章目录

欧拉法
后退的欧拉方法
梯形方法
改进欧拉公式
补充

9.1引言
科学技术中的很多问题可以使用常微分方程的定解描述，包括初值问题以及边值问题两个大类。考虑一阶常微分方程的初值问题，

\in[x_0,b],y(x_0)=y_0.

如果存在实数

L > 0

,使得

|f(x,y_1)-f(x,y2)|\leq L|y_1-y_2|,\forall y_1,y_2\in R,

则称f关于y满足利普西茨条件，

L

为

f

的利普西茨常数。 定理1(唯一性)： 设

f

在区域

D=\{(x,y)|a\leq x\leq b,y \in R\}

上连续，关于y则满足利普西茨条件，则对任意

x_0\in[a,b],y_0\in R

，常微分的初值问题在

x\in[a,b]

上存在唯一的连续可微解

y (x)

。 定理2(敏感性的分析)： 设

f

在区域

D

上连续，且关于y满足利普西茨条件，设初值问题

y'(x)=f(x,y),y(x_0)=s

的解为

y (x, s)

，则

|y(x,s1_1)-y(x,s_2)|\leq e^{L|x-x_0|}|s_1-s_2|

。显然，当

L

较大时认为坏条件，当

L

较小时认为好条件。实际问题之中遇到的常微分方程大部分没有解析解，所以主要依靠数值解法。
9.2简单的数值解法
9.2.1欧拉法与后退欧拉法

欧拉法

欧拉方法：使用公式 $y_{n+1}=y_n+hf(x_n,y_n)$ 逐次地推导算出最终结果。
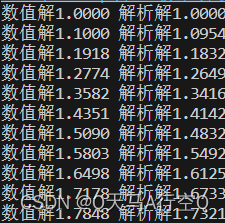
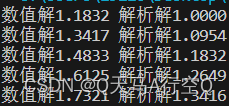
例1：求解初值问题
$\left\{\begin{matrix}y'=y-\frac{2x}{y},0<x<1,\\y(0)=1.\end{matrix}\right.$
得到：
$y_{n+1}=y_n+h(y_n-\frac{2x_n}{y_n})$

def func(x,y):
    if x==None:
        return 1
    return y+0.1*(y-2*x/y)
x_initial,y_initial=None,None
for i in range(11):
    y_initial=func(x_initial,y_initial);x_initial=i/10
    print("数值解{:.4f} 解析解{:.4f}".format(y_initial,pow(1+2*i/10,0.5)))

在这里插入图片描述

%func1
function y_initial=func1(x, y)
    if isempty(x)
        y_initial=1;
    else
        y_initial=y+0.1*(y-2*x/y);
    end
end

%oulafa
x_initial=[];
y_initial=[];
for i=0:10
    y_initial=func1(x_initial,y_initial);
    x_initial=i/10;
    fprintf("数值解%.4f 解析解%.4f\n",y_initial,power(1+2*i/10,0.5));
end

分析欧拉方法误差：通过对 $y_{n+1}$ 进行泰勒二阶展开。 $y(x_{n+1})=y(x_n)+y'(x_n)h+\frac{y''(\xi_n)}{2!}h^2$ 。称 $y(x_{n+1})-y(x_n)=y'(x_n)h+\frac{y''(\xi_n)}{2!}h^2$ 此方法为局部截断误差。另外一种分析方法：我们对 $\in[x_0,b]$ 进行微分。 $y(x_{n+1})+y(x_n)=\int^{x_{n+1}}_{x_n}f(t,y(t))dt$ 。如果使用左矩形公式则可以得到上述公式，如果使用右矩形公式则可以得到另外一公式 $y_{n+1}=y_n+hf(x_{n+1},y_{n+1})$ 。称为后退的欧拉法。后退的欧拉方法是隐式，欧拉方法则是显式。

后退的欧拉方法

设用欧拉公式 $y_{n+1}^{(0)}=y_n+hf(x_n,y_n)$ 给出迭代初值 $y_{n+1}^{(0)}$ 不断迭代则得到 $y_{n+1}^{(k+1)}=y_n+hf(x_n,y_n^{(k)})，k=0,1,\dots,n$ 。只要 $h L$ <1就可以收敛到解 $y_{n+1}$ 了。误差分析同欧拉方法是差不多的。我们这里使用例4进行演示同时探讨两个方法绝对稳定性以及绝对稳定域。
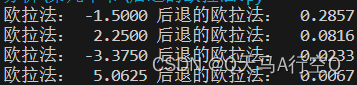
例4：求解初值问题
$\left\{\begin{matrix}y'=-100y,\\y(0)=1.\end{matrix}\right.$
可以解得：
$y(x)=e^{-100x}$

lt1=[]
x_initial=0;y_initial=1
for i in range(4):
    y_initial=y_initial+1/40*(-100*y_initial);x_initial=i/40
    lt1.append(y_initial)
lt2=[]
x_initial=0;y_initial=1
for i in range(4):
    y_initial=y_initial/(1+100*0.025)
    lt2.append(y_initial)
for i in range(4):
    print("欧拉法：{:>8.4f} 后退的欧拉法：{:>8.4f}".format(lt1[i],lt2[i]))

在这里插入图片描述

lt1=[];
x_initial=0;
y_initial=1;
for i=0:3
    y_initial=y_initial+1/40*(-100*y_initial);
    x_initial=i/40;
    lt1=[lt1,y_initial];
end
lt2=[];
x_initial=0;
y_initial=1;
for i=0:3
    y_initial=y_initial/(1+100*0.025);
    lt2=[lt2,y_initial];
end
for i=1:4
    fprintf("欧拉法：%8.4f 后退的欧拉法：%8.4f\n",lt1(i),lt2(i));
end

可以看到 $h$ 为0.025时，欧拉法不稳定但是后退的欧拉法稳定。 $h$ 为0.005时，欧拉法变稳定(这个部分我没有做)。所以得出结论稳定性不仅与方法还与步长有关。现在我们来具体地探讨欧拉方法的稳定性。模型方程 $y'=\lambda y$ 的欧拉公式为 $y_{n+1}=(1+h\lambda)y_n$ 。设在节点 $y_n$ 有一扰动值 $\epsilon_n$ ，在 $y_{n+1}$ 产生大小为 $\epsilon_{n+1}$ 扰动值。所以有 $\epsilon_{n+1}=(1+h\lambda)\epsilon_n$ 。假设差分方程解是不增长的，根据稳定性的定义有 $|1+h\lambda|\leq1$ 。对于后退的欧拉法有 $y_{n+1}=\frac{1}{1-h\lambda}y_n$ 则 $|\frac{1}{1-h\lambda}|<1$ 则稳定域为 $|1-h\lambda|>1$ 。

梯形方法

使用 $y_{n+1}=y_n+\frac{h}{2}[f(x_n,y_n)+f(x_{n+1},y_{n+1})]$ 为公式作为单步推导的方法叫梯形方法。求解方法等同后退的欧拉法。
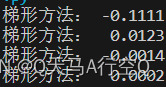
使用例4作为演示(就是上面的那一个)

lt=[]
x_initial=0;y_initial=1
for i in range(4):
    y_initial=(1-50*0.025)*y_initial/(1+50*0.025)
    lt.append(y_initial)
for i in range(4):
    print("梯形方法：{:>8.4f}".format(lt[i]))

在这里插入图片描述

lt=[];
x_initial=0;
y_initial=1;
for i=0:3
    y_initial=(1-50*0.025)*y_initial/(1+50*0.025);
    lt=[lt,y_initial];
end
for i=1:4
    fprintf("Trapezoidal method: %8.4f\n",lt(i));
end

同样我们这里讨论梯形方法的稳定性： $y_{n+1}=\frac{1-\frac{h}{2}\lambda}{1+\frac{h}{2}\lambda}y_{n+1}$ 则 $|\frac{1-\frac{h}{2}\lambda}{1+\frac{h}{2}\lambda}|\leq1$ ，同时这里，我们给出一个定义： 如果一个数值方法的稳定域包含了 $\{h\lambda|Re(h\lambda)<0|$ ，那么称此方法是A-稳定的。后退的欧拉法以及梯形方法都是A-稳定的不需要考虑步长 $h$ 。

改进欧拉公式

先用一次欧拉公式得到 $y_n$ 值，因为效果可能很差所以使用梯形公式进行校准。公式如下，十分简单：
$\left\{\begin{matrix}预测\;\bar{y}_{n+1}=y_n+hf(x_n,y_n),\\\\校正\;y_{n+1}=y_n+\frac{h}{2}[f(x_n,y_n)+f(x_{n+1},\bar{y}_{n+1})].\end{matrix}\right.$
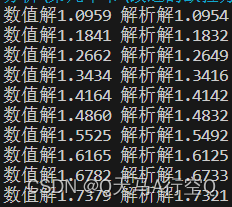
我们使用例2演示：emmm，这个例2就是让你使用改进欧拉方法做遍例1，题目欧拉法那已经写了我就不再写了。

def func(x,y):
    y1=y+0.1*(y-2*x/y)
    y2=y+0.1/2*(y-2*x/y+y1-2*(x+0.1)/y1)
    return y2
x_initial,y_initial=0,1
for i in range(1,11):
    y_initial=func(x_initial,y_initial);x_initial=i/10
    print("数值解{:.4f} 解析解{:.4f}".format(y_initial,pow(1+2*i/10,0.5)))

在这里插入图片描述

%func2
function y2=func2(x,y)
    y1=y+0.1*(y-2*x/y);
    y2=y+0.1/2*(y-2*x/y+y1-2*(x+0.1)/y1);
end

%gaijindeoulagongshi
x_initial=0;
y_initial=1;
for i=1:10
    y_initial=func2(x_initial,y_initial);
    x_initial=i/10;
    fprintf("数值解%.4f 解析解%.4f\n",y_initial,power(1+2*i/10,0.5));
end

这个的稳定域还得看 $f (x, y)$ (这句话可能有问题，我不是特别地确定)。

现在我们讨论一下单步法局部稳定性和阶。显式单步法的局部截断误差： $T_{n+1}=y(x_{n+1})-y(x_n)-h\varphi(x_n,y(x_n),h)$ 。欧拉法的局部截断误差为 $T_{n+1}=y(x_{n+1})-y(x_n)-hf(x_n,y(x_n))=\frac{h^2}{2}y''(x_n)+O(h^3)$ (泰勒展开，简单得很)。然后两个一般概念，P阶精度以及局部误差主项。这两个定义我感觉还是挺重要的，鉴于篇幅原因还是请回到书本吧。

现在我们讨论一下单步法收敛性与相容性。数值解法基本思想：将微分方程化为差分方程吧。好了这里好像一大堆的公式，鉴于篇幅原因还是请回到书本吧。其实感觉可以不用去看推导。知道有就好了。数值方法收敛性的定义；关于收敛性的定理；相容定义；判断相容与否定理。

补充

补充内容感觉不考但是工程中都挺重要的，所以还是来做做吧。这个部分知识点还是自己研究吧。我用Py做一下例题。

龙格—库塔方法

例3：使用4阶龙格库塔方法求解例1

def K1(x,y):
    return y-2*x/y
def K2(x,y):
    return y+0.2/2*K1(x,y)-(2*x+0.2)/(y+0.2/2*K1(x,y))
def K3(x,y):
    return y+0.2/2*K2(x,y)-(2*x+0.2)/(y+0.2/2*K2(x,y))
def K4(x,y):
    return y+0.2*K3(x,y)-(2*(x+0.2))/(y+0.2*K3(x,y))
x,y=0,1
for i in range(5):
    y=y+0.2/6*(K1(x,y)+2*K2(x,y)+2*K3(x,y)+K4(x,y));x+=0.2
    print("数值解{:.4f} 解析解{:.4f}".format(y,pow(1+2*i/10,0.5)))

在这里插入图片描述

%K4
function k4=K4(x,y)
    k3=K3(x,y);
    k4=y+0.2*k3-(2*(x+0.2))/(y+0.2*k3);
end

%K3
function k3=K3(x,y)
    k2=K2(x,y);
    k3=y+0.2/2*k2-(2*x+0.2)/(y+0.2/2*k2);
end

%K2
function k2=K2(x, y)
    k1=K1(x,y);
    k2=y+0.2/2*k1-(2*x+0.2)/(y+0.2/2*k1);
end

%K1
function k1=K1(x, y)
    k1=y-2*x/y;
end

%longgekuta
x=0;
y=1;
for i=1:5
    k1=K1(x,y);
    k2=K2(x,y);
    k3=K3(x,y);
    k4=K4(x,y);
    y=y+0.2/6*(k1+2*k2+2*k3+k4);
    x=x+0.2;
    fprintf("数值解%.4f 解析解%.4f\n",y,power(1+2*(i-1)/10,0.5));
end

PS1：我这样写效率不高因为重复算了很多东西，可以自己试着修改。
PS2：可以自己试着求解四阶龙格库塔方法的稳定域(直接让你浪费生命的10分钟)。

线性多步法

在逐步推进求解过程中，计算 $y_{n+1}$ 之前事实上已经求出了一系列近似值 $y_0,y_1,\dots,y_n$ ，如果充分利用前面多步信息预测 $y_{n+1}$ 则可以获得较高精度。一般的线性多步法公式表示为 $y_{n+k}=\sum\limits_{i=0}^{k-1}\alpha_iy_{n+i}+h\sum\limits_{i=0}^k\beta f_{n+i}$ 。还是有必要看一下线性多步法的构造途径但是这里我们不再过多赘述。感觉原书这一部分排版不是很好。

阿当姆斯显示与隐式公式

考虑形 $y_{n+k}=y_{n+k-1}+h\sum\limits_{i=0}^k\beta_if_{n+i}$ $的 k$ 步法，称为阿当姆斯方法。当 $\beta_k$ 为0时，显示方法；不为0时，隐式方法。
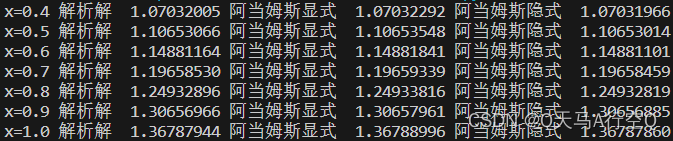
例6：使用四阶阿当姆斯显示以及隐式方法求初值问题 $y = - y + x + 1, y (0) = 1$ ，取步长 $h = 0.1$ 。

import math
lt1=[]
def func1():
    for i in range(11):
        lt1.append(pow(math.e,-i/10)+i/10)
func1()
def f(x,y):
    return -y+x+1
lt2=lt1[:4]
def func2():
    for i in range(4,11):
        lt2.append(lt2[-1]+0.1/24*(55*f(i/10-0.1,lt2[-1])-59*f(i/10-0.2,lt2[-2])+37*f(i/10-0.3,lt2[-3])-9*f(i/10-0.4,lt2[-4])))
func2()
lt3=lt1[:3]
def func3():
    for i in range(3,11):
        lt3.append(1/24.9*(22.1*lt3[-1]+0.5*lt3[-2]-0.1*lt3[-3]+0.24*(i-3)+3))
func3()
for i in range(4,11):
    print("x={:.1f}".format(i/10),end=" ")
    print("解析解{:>12.8f} 阿当姆斯显式{:>12.8f} 阿当姆斯隐式{:>12.8f}".format(lt1[i],lt2[i],lt3[i]))

在这里插入图片描述

%f
function result=f(x,y)
    result=-y+x+1;
end

%f1
function lt=f1()
    lt=zeros(1,11);
    for i=0:10
        lt(i+1)=exp(-i/10)+i/10;
    end
end

%f2
function lt2=func2(lt1)
    lt2=lt1(1:4);
    for i=4:10
        lt2(i+1)=lt2(i)+0.1/24*(55*f(i/10-0.1,lt2(i))-59*f(i/10-0.2,lt2(i-1))+37*f(i/10-0.3,lt2(i-2))-9*f(i/10-0.4,lt2(i-3)));
    end
end

%f3
function lt3=func3(lt1)
    lt3=lt1(1:3);
    for i=3:10
        lt3(i+1)=1/24.9*(22.1*lt3(i)+0.5*lt3(i-1)-0.1*lt3(i-2)+0.24*(i-3)+3);
    end
end

%xianxingduobufa
lt1=f1();
lt2=f2(lt1);
lt3=f3(lt1);
for i=4:10
    fprintf("x=%.1f ",i/10);
    fprintf("解析解%12.8f 阿当姆斯显式%12.8f 阿当姆斯隐式%12.8f\n",lt1(i+1),lt2(i+1),lt3(i+1));
end

搞定。