Bootstrap

动态规划：0-1背包问题

0-1背包问题

给定n个容量为 W 1 W_1 W1​， W 2 W_2 W2​， W 3 W_3 W3​, 。。。 W n W_n Wn​，价值为 V 1 V_1 V1​, V 2 V_2 V2​， V 3 V_3 V3​, … V n V_n Vn​的物品和容量为C的背包，求这个物品中一个最有价值的子集，使得在满足背包的容量的前提下，包内的总价值最大。

为什么要叫做0-1背包： 因为对每个物品而言，只有两种选择，盘它或者不盘，盘它记为1，不盘记为0，我们不能将物品进行分割，比如只拿半个是不允许的。这就是这个问题被称为0/1背包问题的原因。

int maxValue(const std::vector<int>& w,  const std::vector<int>& v, int bag){

}

解决这个问题没有什么巧妙的算法，只能穷举所有的可能。因此解决这类问题，直接根据套路走流程即可。

暴力递归

先从左往右依次尝试。举个例子，比如有物品[0, 1, 2]，那么对每一个物品都去拿或者不拿

class Solution {
public:
    // 前提：w，v都是正数 或者 零
    // bag为背包容量，不能超过这个载重
    // 返回：不超重的情况下，能够得到的最大价值
    int maxValue(const std::vector<int>& w,  const std::vector<int>& v, int bag){
        // 去掉不合法的参数
        if(w.empty() || v.empty() || w.size() != v.size() || bag < 0){
            return 0;
        }

        // 写一个尝试函数
        return process(w, v, 0, bag);
    }

private:
    // 当前考虑到了index号货物，从index....所有的货物可以自由选择（index就当做没有了）
    // 但是做的选择不能超过背包容量
    // 返回：最大价值
    int process(const std::vector<int>& w, const std::vector<int>& v, int index, int rest){
        // base case:
        // 背包容量已经小于0，那么从当前index开始之后的货物都不能选择了，因为背包一定超重
        if(rest < 0){ // 为什么不需要等于0. 因为根据题意，允许货物重量0
            return 0;
        }
        // 当没有货物了，价值是0
        if(index == w.size()){
            return 0;
        }

        // 当前有货物，而且背包有容量
        // 尝试1：不要当前的货物
        int p1 = process(w, v, index + 1, rest);
        // 尝试2：要当前的货物
        int p2 = 0;
        if(rest >= w[index]){ // 只有在背包容量大于当前货物容量时，才可以去要当前的货物
            p2 = v[index] + process(w, v, index + 1, rest- w[index]) ;
        }

        // 上面两种决策中选择一个好的
        return std::max(p1, p2);
    }



};

int main(){
    Solution a;
    std::vector<int> w {3, 2, 4, 7};
    std::vector<int> v {5, 6, 3, 19};
    std::cout << a.maxValue(w, v, 11);  // 25
}

暴力递归改动态规划

（1）先举个例子，看暴力递归有没有重复调用，有，所以可以改成递归

（2）准备一个表。重点关注可变参数的范围

int process(const std::vector<int>& w, const std::vector<int>& v, int index, int rest)
  • index：是物品的范围------ index == w.size()------0~N
  • rest：是背包剩余容量------ bag < 0------负数~bag（负数可以过滤）

所以，准备一个二维数组：

std::vector<std::vector<int>> dp(N + 1, std::vector<int>(bag + 1));

（3）返回值，关注主函数是怎么调用的：

return process(w, v, 0, bag);

所以，应该返回dp[0][bag]

（4）接下来就该填表了

怎么填写呢？举个例子，然后根据上面的暴力递归

  • 先填表base case，并标记target
  • 然后看依赖
    • process(w, v, index + 1, bag - w[index]) ;
    • 从下到上，（从左到右和从右到左都可以）
class Solution {
public:
    // 前提：w，v都是正数 或者 零
    // bag为背包容量，不能超过这个载重
    // 返回：不超重的情况下，能够得到的最大价值
    int maxValue(const std::vector<int>& w,  const std::vector<int>& v, int bag){
        // 去掉不合法的参数
        if(w.empty() || v.empty() || w.size() != v.size() || bag < 0){
            return 0;
        }

        int  N = w.size();
        std::vector<std::vector<int>> dp(N + 1, std::vector<int>(bag + 1, 0));
        for (int index = N - 1; index >= 0; index--) { // 从最后一个物品开始看
            for (int rest = 0; rest <= bag; rest++){ // 背包容量
                int p1 = dp[index + 1][rest];
                int p2 = 0;
                if(rest >= w[index]){
                    p2 = v[index] + dp[index + 1][rest - w[index]];
                }
                dp[index][rest] = std::max(p1, p2);
            }
        }
        return dp[0][bag];
    }

};

动态规划

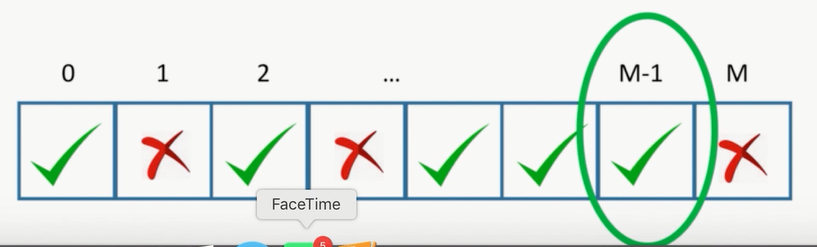
  • 因为物品的重量都是整数，每个装物品的方案的总重量都是0-N
  • 如果对于每个总重量，我们能知道有没有方案能做到，就可以解决
    在这里插入图片描述

（1）确定状态

  • 需要知道N个物品是否能拼出重量W（W=0…M）
  • 最后一步：最后一个物品(重量 A N − 1 A_{N-1} AN−1​)是否进入背包
    • 情况一：如果前N-1个物品能拼出W，那么前N个物品也能拼出W
    • 情况二：如果前N-1个物品能拼出 W − A N − 1 W-A_{N-1} W−AN−1​，那么最后加上物品 A N − 1 A_{N-1} AN−1​，拼出W
  • 子问题：
    • 要求前N个物品能不能拼出重量0…M
    • 就需要知道前N-1个物品能不能拼出重量0…M
  • 状态：
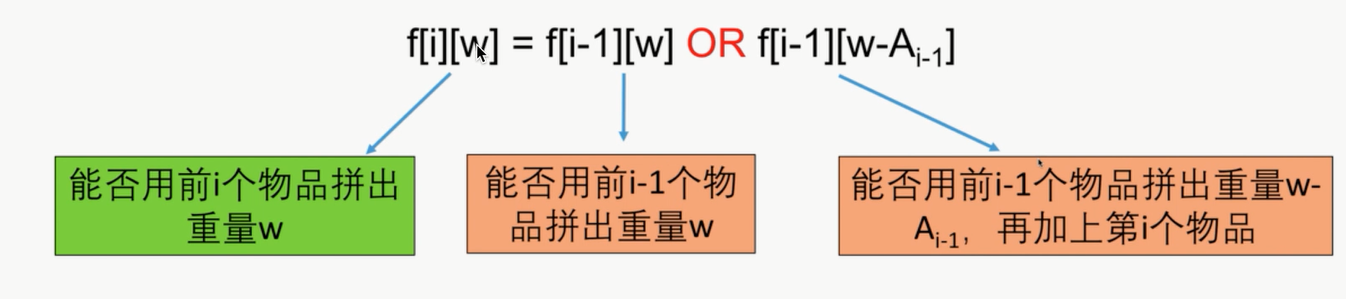
    • 设f[i][w]=能否用前i个物品拼出重量W(true/false)

（2）转移方程
在这里插入图片描述

（3）初始状态和边界情况

在这里插入图片描述

（4）计算顺序

  • 从左到右，从小到大

在这里插入图片描述

小结：

  • 要求不超过target时能拼出的最大重量
  • 需要记录前i个物品能拼出哪些重量
  • 前i个物品能拼出的重量
    • 前i-1个物品能拼出的重量
    • 前i-1个物品能拼出的重量 + 第i个物品重量

动态规划

问题建模

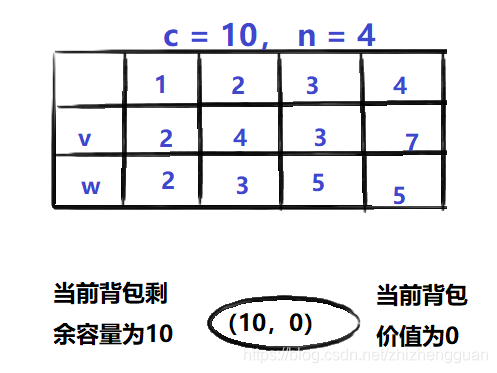
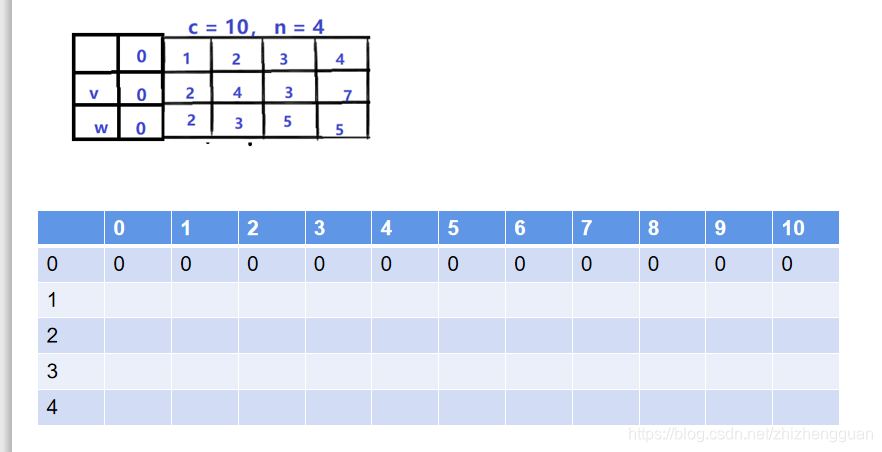
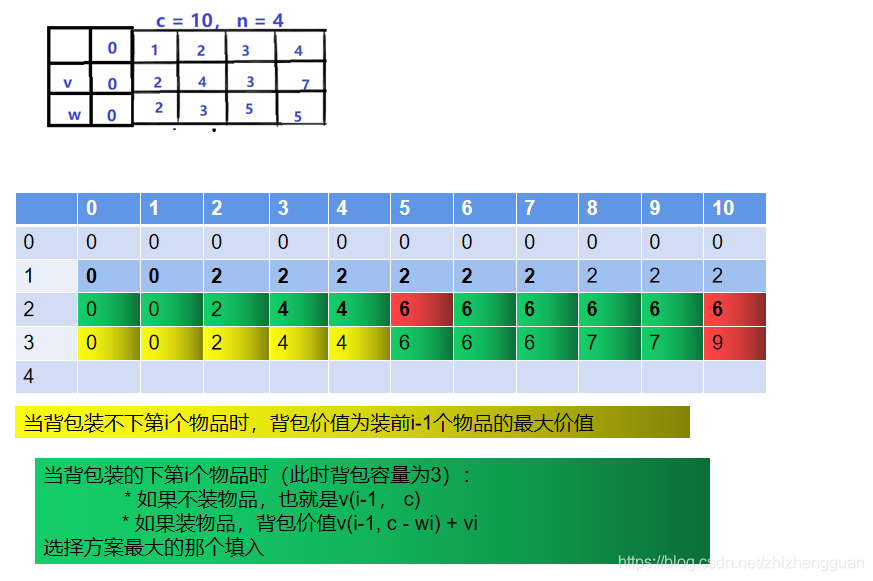
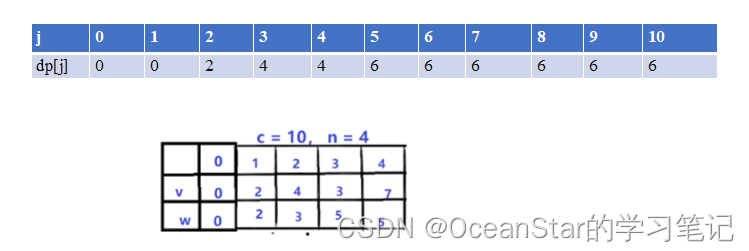
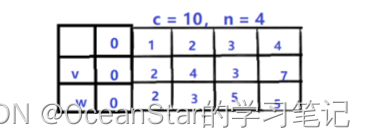
假设有四个物品，它们的价值和体积如下图所示：
在这里插入图片描述

（0）分析：当前有三个变化维度：第N个物品，背包的容量W、总的背包的价值V。

  • 其中，目标是要使得背包价值达到最大。
  • 所以，一共有两个变化维度，因此需要定义一个二维向量V(n, w)

（1）这个问题的最优子结构

  • 假设我们只剩下最后一个也就是第4个物品要考虑了，这时候会出现几种情况呢？
  • 因此，问题的最优子结构如下：
    • 没有足够的空间了，此时一定不能装。
      • 不装：此时答案是：前3个物品，10容量的最大价值
    • 有足够的空间，此时可以选择装或者不装
      • 装：此时答案是： 第4个物品的价值 + 前3个物品，10-5容量的最大价值
    • 总结：问题的最优子结构有两个
      • 当所剩容量不足以装载当前物品时，只有一种最优子结构
        • 不选：前3个物品，10容量的最大价值
      • 当所剩容器足以装载当前物品时，有两种最优子结构
        • 不选：前3个物品，10容量的最大价值
        • 选： 前3个物品，10-5容量的最大价值

（2）推导状态转移方程。。要推导状态转移方程，就是要推导最优子结构和最终问题有什么关系呢？也就是说，3个金矿的最优选择和4个金矿的最优选择之间，是什么样的关系？

  • 关系：
    • 当容量不够装载第4个物品时，答案肯定是：（前3个物品10容量的最大价值）
    • 当容器足够装载第4个物品时，这时候有两种子结构，需要考虑这两种子结构和最终价值的关系。
      • 有两种子结构，相当于有两种方案，这两种方案的区别在于装或者不装最后一个物品（装不装物品会影响最大价值以及容量），我们需要从中选出一个价值最大的方案
      • 5物品的最优选择 ，就是（前3个物品，10容量的最大价值） 和（ 第4个物品的价值 + 前3个物品，10-5容量的最大价值）之间的最大值
  • 从而可以推导出状态方程
    • 当前有三个变化维度：第N个物品，还剩下的容量W、背包的最大价值V。最大价值是目标，所以它应该是返回值，所以我们需要考虑两个变化维度。用数学语言来模式，就是要求一个二维函数，假设为F(n， w)，n为第几个物品，w为剩下的容量
    • 从而第4物品和第3物品之间的最优选择之间存在这样的关系： F(4， 10) = MAX(F(3， 10)， F(3, 10 - weight(4) + value(4)));

（3）问题的边界

  • 当物品树为0或者工人数为0时，F(n， w) = 0

（4）总结。当前问题的状态转移方程

  • 设F(n，w)为挑选第n个物品、背包容量为w时的最大价值。那么状态转移方程
    • 边界：当物品数量为0或者背包容量为0时，F(n, w) = 0(n = 0或者w = 0)
    • 当所剩容量不足以装载当前物品时，只有一种最优子结构：F(n,w)=F(n-1,w),(n>=1,w<weight[n-1])
    • 常规情况下有两种最优子结构（装和不装）：F(n,w)=max(F(n-1,w),F(n-1,w-p[n-1]+g[n-1])),(n>=1,w>=weight[n-1])

实现分析

题目中一般会给定两个数组以及一个背包容量bagweight

vector<int> weight = {1, 3, 4};
vector<int> value = {15, 20, 30};

每次我们都往weight以及value中前插一个数字

vector<int> weight = {0, 1, 3, 4};
vector<int> value = {0, 15, 20, 30};

以补足边界条件没有物品时，或者没有背包容量时的情况

（1）确定dp数组以及下标的含义

  • dp[i][j]：从下标为[0-i]的物品里任意取（每选择一个会减去一些重量），放进容量为j的背包，价值总和最大是多少。
  • i的长度为weight.size()，j的长度为bagweight + 1
  • 返回值：dp[weight.size(） - 1][ bagweight]：

（2）确定递归公式。面对第i个物品

  • 当j < weight[i]时，dp[i][j] =dp[i - 1][j]
  • 否则，dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);

（3）dp数组如何初始化

for (int i = 0 ; i < dp.size(); j++) {  
    dp[i][0] = 0;
}

for (int j = 0 ; i < dp[0].size(); j++) {  
    dp[0][j] = 0;
}

（4）确定遍历顺序

  • 我们知道dp[i][j]，有两个变化维度，i表示物品，j表示背包重量。那么怎么变量呢？一般来讲，我们都是遍历物品的（虽然两个都可以）
  • 由递推公式dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i])，我们知道dp[i][j]要靠左上来推导，所以要从左到右，从上到下遍历

（5）举例推导dp数组

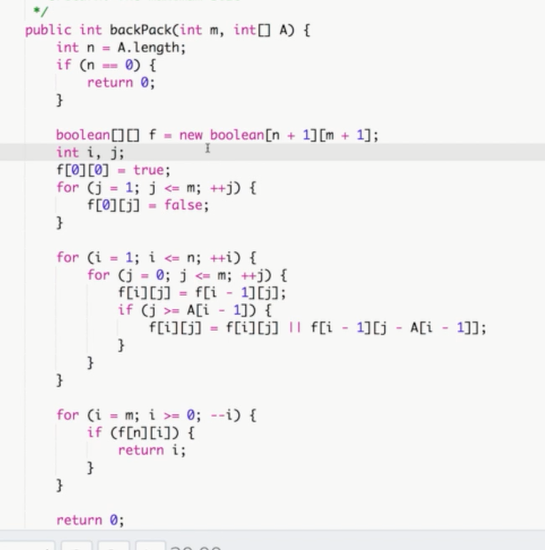
代码：

class Solution {
public:
    void bag_problem(vector<int> weight, vector<int> value, int bagweight) {
        if(weight.empty() || bagweight == 0){
            return;
        }
        weight.insert(weight.begin(), 0);
        value.insert(value.begin(), 0);
        vector<vector<int>> dp(weight.size(), vector<int>(bagweight + 1, 0));


        int m = dp.size(), n = dp[0].size();
        for(int i = 1; i < m; i++) { // 遍历物品
            for(int j = 1; j < n; j++) { // 遍历背包容量
                if (j < weight[i]) {
                    dp[i][j] = dp[i - 1][j];
                }else {
                    dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
                }
            }
        }

        cout << dp[m - 1][n - 1] << endl;
    }
};

空间优化

前提

在使用二维数组的时候，递推公式：dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);

可以看出，如果把dp[i - 1]那一层直接拷贝到dp[i]上，表示完全可以是dp[i][j] = max(dp[i][j], dp[i][j - weight[i]] + value[i]);

与其把dp[i - 1] 这一层拷贝到dp[i]上，不如直接只用一个一维数组了，只用dp[j]（一维数组，也可以理解是一个滚动数组）。

这就是滚动数组的由来。需要满足的条件是上一层可以重复利用，直接拷贝到当前层。

实现

  1. 确定dp数组的含义
  • dp[i][j]表示从下标为[0-i]的物品里任意选取，放进容量为j的背包，价值总和最大为多少
  • dp[j]表示，容量为j的背包，所背的物品价值可以最大为dp[j]
  1. 确定一维dp数组的递推公式
  • dp[j]为容量为j的背包所背的最大价值，那么如何推导dp[j]呢？
  • 对于dp[j]和物品i，有两种选择：
    • 不放物品i，此时价值不变，仍然为dp[j]
    • 装载物品j，此时dp[i] = dp[j - weight[i]] + value[i]， 表示容量为j-物品i重量的背包加锁物品的价值
  • 此时我们应该从这两个方案中选择一个最大的：dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
  1. dp数组如何初始化
  • dp[j]表示容量为j的背包，所背的物品价值最大为dp[j]。
  • 因此dp[0]应该为0，因为容量为0时，不能背东西，所以价值为0
  • 那么dp数组除了下标0的位置，初始为0，其他下标应该初始化多少呢？
    • 根据递归公式：dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
    • dp数组在推导的时候一定是取价值最大的数，如果题目给的价值都是正整数那么非0下标都初始化为0就可以了。这样才能让dp数组在递归公式的过程中取的最大的价值，而不是被初始值覆盖了。
    • 这里假设物品价值都是大于0的，所以dp数组初始化的时候，都初始为0就可以了
  1. 一维dp数组遍历顺序

  • 这里还是有两个变化维度，物品、背包容量，所以需要一个双重for循环以枚举所有的可能

  • 二维数组遍历时：

        for(int i = 1; i < m; i++) { // 遍历物品
            for(int j = 1; j < n; j++) { // 遍历背包容量
                if (j < weight[i]) {
                    dp[i][j] = dp[i - 1][j];
                }else {
                    dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
                }
            }
        }
  • 从上面可以看出，二维数组遍历时，遍历背包的顺序是不一样的：二维数组背包容量是从小到大，一维数组遍历时背包容量是从大到小
    • 为什么呢？从后往前循环，每次取得状态不会和之前取得状态重合，这样可以保证物品i只能被放入一次。如果正序遍历的话，物品会被重复放入多次。
    • 为什么二维dp数组历的时候不用倒序呢？dp[i][j]都是通过上一层即dp[i - 1][j]计算而来，本层的dp[i][j]并不会被覆盖！
  • 两个嵌套for循环的顺序，可以先遍历物品在遍历背包容量，那可不可以先遍历背包容量嵌套遍历物品呢？不可以，因为一维dp的写法，背包容量一定是要倒序遍历（原因上面已经讲了），如果遍历背包容量放在上一层，那么每个dp[j]就只会放入一个物品，即：背包里只放入了一个物品。
class Solution {
public:
    void bag_problem(vector<int> weight, vector<int> value, int bagweight) {
        if(weight.empty() || bagweight == 0){
            return;
        }
        weight.insert(weight.begin(), 0);
        value.insert(value.begin(), 0);


        vector<int> dp(bagweight + 1, 0);


        int m = dp.size();
        for(int i = 1; i < m; i++) { // 遍历物品
            for (int j = bagweight; j >= weight[i]; --j) {  // 遍历背包容量
                dp[j] = std::max(dp[j], dp[j - weight[i]] + value[i] );
            }
        }

        cout << dp[bagweight] << endl;
    }
};

数学分析

在解决问题之前，为了描述方便，我们先定义一些变量，把背包问题抽象化：

  1. 使用变量 X i ，取值为 0 或者 1 ，表示第 i 个物品选择或者不选择 使用变量X_i， 取值为0或者1，表示第i个物品选择或者不选择 使用变量Xi​，取值为0或者1，表示第i个物品选择或者不选择
  2. V n 表示第 n 个物品的价值， W n 表示第 n 个物品的体积，一个有 N 个物品 V_n表示第n个物品的价值， Wn表示第n个物品的体积，一个有N个物品 Vn​表示第n个物品的价值，Wn表示第n个物品的体积，一个有N个物品

明确要解决的问题，也就是说我们要操作N个物品，选出能够达到最大价值的最佳组合：

  1. 需要求解 m a x ( V 1 X 1 + V 2 X 2 + . . . + V n X n ) max(V_1X_1+V_2X_2+...+V_nX_n) max(V1​X1​+V2​X2​+...+Vn​Xn​)

明确约束条件

  1. W 1 X 1 + W 2 X 2 + . . . . . . + W n X n < C W_1X_1+W2_X2+......+W_nX_n < C W1​X1​+W2X​2+......+Wn​Xn​<C
  • 定义函数 V ( i , j ) V(i,j) V(i,j)：代表当前背包剩余容量为j时，前i个物品最佳组合所对应的价值

对于第i个物品，有两种可能

  • 背包剩余容量不足以容纳该物品，此时背包的价值和前i-1个物品的价值是一样的：
    V ( i , j ) = V ( i − 1 , j ) V(i, j) = V(i-1, j) V(i,j)=V(i−1,j)
  • 包剩余容量可以装下该商品，此时需要进行判断，因为装了该商品不一定能使最终组合达到最大价值，所以在装和不装之间选择最优的一个，也就是 V ( i , j ) = m a x ( V ( i − 1 , j ) , V i + V ( i − 1 , C − W i ) ) V(i, j) = max(V(i-1, j), V_i + V(i-1, C- W_i)) V(i,j)=max(V(i−1,j),Vi​+V(i−1,C−Wi​))

总结：
V ( i , j ) = { V ( i − 1 , j ) ,    W i > j m a x ( V ( i − 1 , j ) , V i + V ( i − 1 , C − W i ) ) ,    W i < = j V(i, j) = \begin{cases} V(i-1, j) ,\,\, W_i >j\\ max(V(i-1, j), V_i + V(i-1, C- W_i)),\,\,W_i <=j\\ \end{cases} V(i,j)={V(i−1,j),Wi​>jmax(V(i−1,j),Vi​+V(i−1,C−Wi​)),Wi​<=j​

golang填表

package main

import "fmt"

func max(x, y int)int  {
	if x > y {
		return x
	}
	return y
}

var v [5]int = [5]int {0,2,4,3,7};			
var w [5]int  = [5]int {0,2,3,5,5 };			

const N  int = 4 // 物品个数
const C  = 10  // 背包大小

var dp_table [N + 1][C + 1 ]int ; // N + 1 和 C + 1是为了补充当背包装入物品 / 背包容量为0 时的状态


func show_table()  {
	for j := 0; j <= C ; j++  {
		fmt.Printf("%5d",j)
	}
	fmt.Println("\t | \n-------------------------------------------------------------------------")

	for i := 0; i <= N ; i++  {
		for j := 0; j <= C ; j++  {
			fmt.Printf("%5d",dp_table[i][j])
		}
		fmt.Println("\t | ", i)
	}
}

func findMax()  {
	for i := 1; i <= N ; i++  { // 当面对第i号物品时
		for j := 1; j <= C  ; j++ { // 背包容量  1，2，3。。。。。
			//dp_table[i][j]表示当背包容量为j时，前j个物品组合起来的最大价值 
			if  j < w[i] { // 装不下时
				dp_table[i][j] = dp_table[i-1][j];  // 背包容量为j时，前i个物品的最大价值就是前i-1个物品的最佳价值。 因为i从1开始，所以不用担心越界
			}else{ // 装的下
				dp_table[i][j] = max(dp_table[i-1][j], v[i] + dp_table[i - 1][j - w[i]]) // 装和不装之间的方案选择一个
				// j - w[i] 表示装了i之后，容量减少的量。因为装得下，所以j - w[i]的最小值为0[也就是刚好装得下]，所以不用担心数组越界
			}
		}
	}
}
func main() {
	findMax()
	show_table()
}

动态规划求解如下：

package main

import "fmt"

const N=4
const W=10

var weight[]int=[]int {0, 2 , 4 , 3 , 7}
var val[] int =  []int{0,  2, 3, 5, 5}
var record[N + 1][W+1]int   //保存中间结果


func show(){  //初始化背包结果
	fmt.Print("  |")
	for j:=0;j<=W;j++{
		fmt.Printf("%5d",j)
	}
	fmt.Println("\n---------------------------------------------------------------")

	for i:=0;i<=N;i++{
		fmt.Printf("%d |", i)
		for j:=0;j<=W;j++{
			fmt.Printf("%5d", record[i][j])
		}
		fmt.Println()
	}

	fmt.Println("**************************************************************")
}
//两个数之间最大值
func max(a int ,b int)int{
	if a>b{
		return a
	}else{
		return b
	}
}
func findMax()int{
	for i:=1;i<=N;i++{
		for j:=weight[i];j<=W;j++{
			record[i][j]=max(record[i-1][j],record[i-1][j-weight[i]]+val[i])
		}
	}

	return record[N][W]
}


func main() {
	show();
	fmt.Println(findMax()) // 10

	show();
}

分治递归[通过具有记忆功能的迭代自顶而下求解]

在解决问题之前，为了描述方便，我们先定义一些变量，

  1. 使用变量 X i ，取值为 0 或者 1 ，表示第 i 个物品选择或者不选择 使用变量X_i， 取值为0或者1，表示第i个物品选择或者不选择 使用变量Xi​，取值为0或者1，表示第i个物品选择或者不选择
  2. V n 表示第 n 个物品的价值， W n 表示第 n 个物品的体积，一个有 N 个物品 V_n表示第n个物品的价值， Wn表示第n个物品的体积，一个有N个物品 Vn​表示第n个物品的价值，Wn表示第n个物品的体积，一个有N个物品

我们先来明确一些问题：

  1. 我们要求解的问题是让背包中的物品总价值达到最大，也就是： m a x ( X 1 V 1 + X 2 V 2 + X 2 V 3 + . . . + X n V n ) max(X_1V_1 + X_2V_2 + X_2V_3 + ... + X_nV_n) max(X1​V1​+X2​V2​+X2​V3​+...+Xn​Vn​)
  2. 约束条件是： X 1 W 1 + X 2 W 2 + X 3 W 3 + . . . + X n W n = < C X_1W_1 + X_2W_2 + X_3W_3 + ... + X_nW_n =< C X1​W1​+X2​W2​+X3​W3​+...+Xn​Wn​=<C
  3. 定义函数 . 用 F ( i , j ) ：代表当前背包剩余容量为 j 时，前 i 个物品最佳组合对应的价值 用F(i , j)：代表当前背包剩余容量为j时，前i个物品最佳组合对应的价值 用F(i,j)：代表当前背包剩余容量为j时，前i个物品最佳组合对应的价值
  • F ( 0 , C ) = 0 F(0, C)=0 F(0,C)=0的意思是：当没有物品放入背包时，不管背包容量多少，其最大价值为0
  • F ( n , 0 ) = 0 F(n, 0)=0 F(n,0)=0的意思时：当背包容量为0时，最大价值一定是0【因为没地方放】

那这里的递推关系式是怎样的呢？对于第i个物品，有两种可能【放得下、放不下】：

  1. 包的容量比该商品体积小，装不下，因此，此时背包的价值与放入i-1个物品的价值是一样的，也就是 F ( i , j ) = F ( i − 1 , j ) F(i, j) = F(i - 1, j) F(i,j)=F(i−1,j)

举个例子：对于F(2, 5)，如果下标2的物品容量为6，大于背包容量，那就不能装了，它的价值一定和F(1, 5)时一样的

也就是说，当第n件物品放不下时，最大价值就是
F ( i , j ) = F ( i − 1 , j ) F(i, j) = F(i - 1, j) F(i,j)=F(i−1,j)

  1. 容量足够，可以放置第n个物品，但是装了也不一定能够达到最优价值，所以在装和不装之间选择最优的一个，也就是 F ( i , j ) = m a x ( F ( i − 1 , j ) , V i + F ( i − 1 , C − W i ) ) F(i, j) = max(F(i-1, j), V_i + F(i-1, C- W_i)) F(i,j)=max(F(i−1,j),Vi​+F(i−1,C−Wi​))

在背包容量足够的前提下， 对于当前物品，有两种选择：【放、不放】

  • 如果选择不放， 问题就转化为将n-1件物品放入容量为j的背包中， 可以得到的最大价值为 F ( i − 1 , j ) F(i-1, j) F(i−1,j)
  • 如果选择放， 那么问题就转换为将i-1个物品放入剩余容量为 C − W i C-W_i C−Wi​的背包中的问题， 此时获取的最大价值为： V i + F ( i − 1 , C − W i ) V_i + F(i-1, C- W_i) Vi​+F(i−1,C−Wi​)
    • 为什么 C − W i C- W_i C−Wi​？因为我们确定了要装i，所以必须至少留出 W i W_i Wi​个空间

也就是说，当物品能够装得下时，我们应该在装和不装之间这两种方案中选择最优的一个，也就是
F ( i , j ) = m a x ( F ( i − 1 , j ) , V i + F ( i − 1 , C − W i ) ) F(i, j) = max(F(i-1, j), V_i + F(i-1, C- W_i)) F(i,j)=max(F(i−1,j),Vi​+F(i−1,C−Wi​))

原问题：将n件物品放入容量为c的背包，得到的最大价值。
子问题是：将i件物品让如容量为j的背包的，得到的最大价值。

package main

import "fmt"

func max(x, y int)int  {
	if x > y {
		return x
	}
	return y
}

var w []int = []int {0, 2 , 4 , 3 , 7 };  // 体积
var v []int  = []int {0, 2 , 3 , 5 , 5 };		 // 价值


// findMax( i, c int)  c表示剩下的背包容量，i表示还剩下的物品数量，也是物体的下标
func findMax(i,  c int) int  {
	result := 0;
	if (i == 0 || c == 0){ // 背包容量为0，或者没有物体了
		return result
	}

	if(w[i] > c){ // 装不下
		result = findMax(i-1, c)  // 当前物品已经排除，需要寻找把i-1个物品放入c的最优选择
	} else { 	// 可以装下
		tmp1 := findMax(i-1, c);  // 选择要
		tmp2 := findMax(i-1, c-w[i]) + v[i];  // 还是不要
		result = max(tmp1, tmp2); // 的最优选择
	}
	return result;
}
func main() {
	c := findMax(4,  10)  // 10
	fmt.Print(c)
}

分治改进

package main

import "fmt"

const N=4
const W=10

var weight[]int=[]int {0, 2 , 4 , 3 , 7}
var val[] int =  []int{0,  2, 3, 5, 5}
var record[N + 1][W+1]int   //保存中间结果

func init(){  //初始化
	for i:=0;i<=N;i++{
		for j:=0;j<=W;j++{
			record[i][j]=-1
		}
	}
}

func show(a, b int){  //初始化背包结果
	fmt.Print("  |")
	for j:=0;j<=W;j++{
		fmt.Printf("%5d",j)
	}
	fmt.Println("\n---------------------------------------------------------------")

	for i:=0;i<=N;i++{
		fmt.Printf("%d |", i)
		for j:=0;j<=W;j++{
			if i == a && b == j {
				fmt.Printf("%c[1;40;32m%5d%c[0m", 0x1B, record[i][j], 0x1B)
			}else{
				fmt.Printf("%5d", record[i][j])
			}

		}
		fmt.Println()
	}

	fmt.Println("**************************************************************")
}
//两个数之间最大值
func max(a int ,b int)int{
	if a>b{
		return a
	}else{
		return b
	}
}
//i是已经有的重量，total总量
func  findMax(i int ,total int )int {
	result:=0//结果
	if i> N{
		return result
	}
	if record[i][total]!=-1{ //如果数据已经记录，直接返回
		fmt.Println("\n\n",i, total, ":")
		show(i, total);
		return record[i][total]
	}
	if weight[i]>total{
		record[i][total]=findMax(i+1,total) //当前物品大于总量，跳出，计算下一个
	}else{
		record[i][total]=max(findMax(i+1,total),findMax(i+1,total-weight[i])+val[i])
	}

	fmt.Println("\n\n",i, total, ":")
	show(i, total);
	return record[i][total]
}




func main() {
	show(-1, -1);
	fmt.Println(findMax(0, W)) // 10
}

dp的填表过程

我们知道，我们必须探究每一个物品放入还是不放入背包的可能性。

  • 每一个物品能不能放入背包
  • 当每一个物品放入背包时有可能面临的空间是0、是1、是2。。。

我们用一个表来记录已经算过的价值

假设有四个物品，它们的价值和体积如下图所示：
在这里插入图片描述
接下来，我们来一一探究

  • 对于表格：

    • 横：表示背包容量
    • 纵：表示物品编号
    • 表格的每一个方格的意义： 当背包容量为 i 时，前 i 个物品最佳组合对应的价值 当 背包容量为i时，前i个物品最佳组合对应的价值 当背包容量为i时，前i个物品最佳组合对应的价值

  • 初始时，不管背包容量空间多少，如果不往里面装东西，背包价值都是0
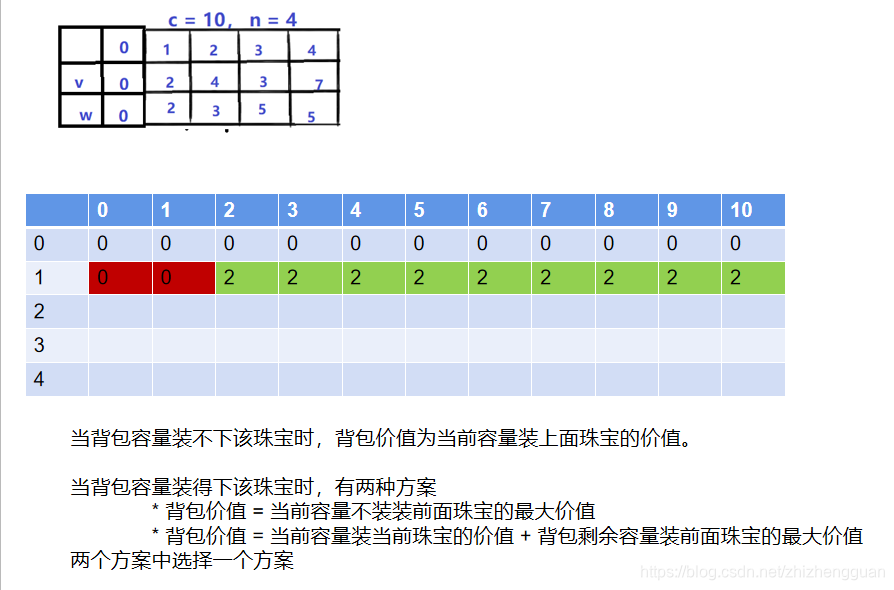
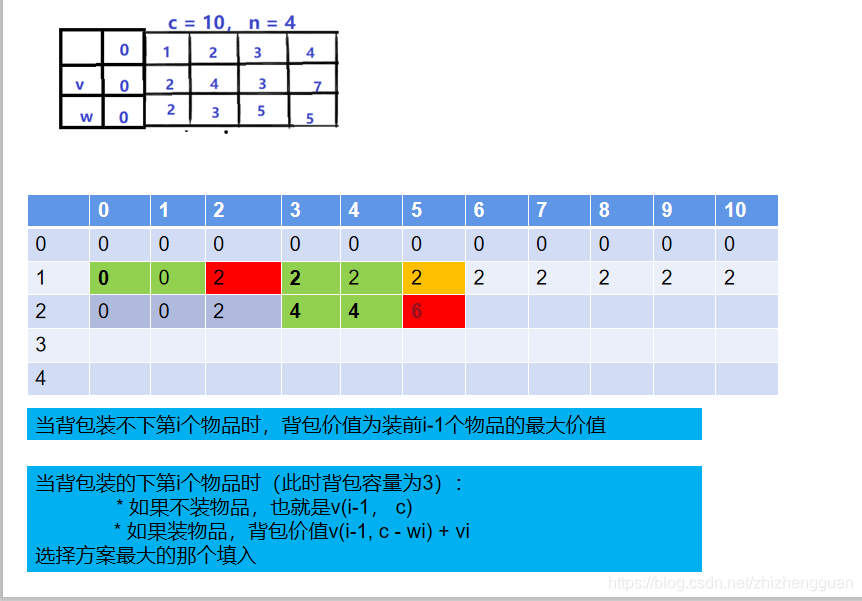
    在这里插入图片描述

  • 当装前1个物品时，背包剩余容量可能是0、1、2、。。。。10，装入之后背包的价值如下
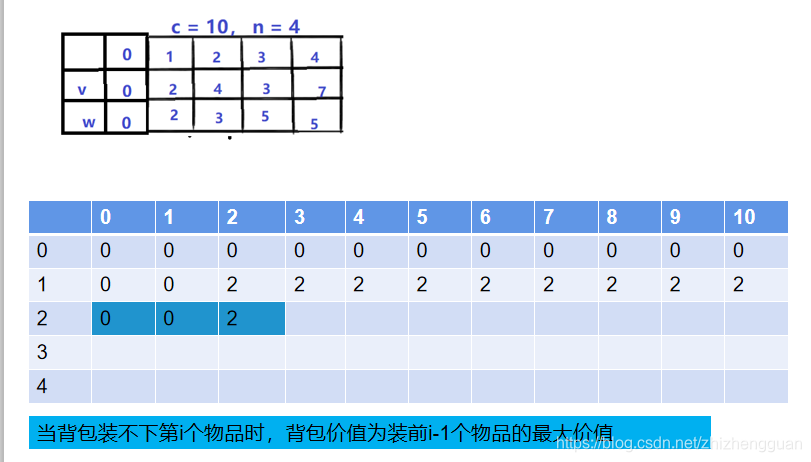
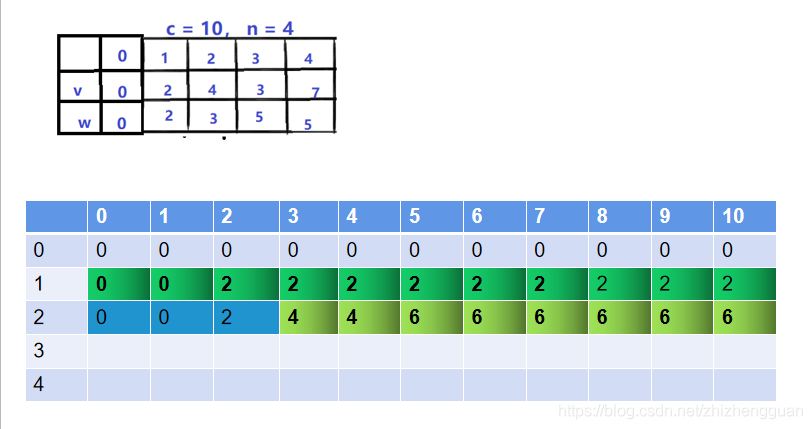
    在这里插入图片描述

  • 当面对前2个物品（也就是1，2号物品）：
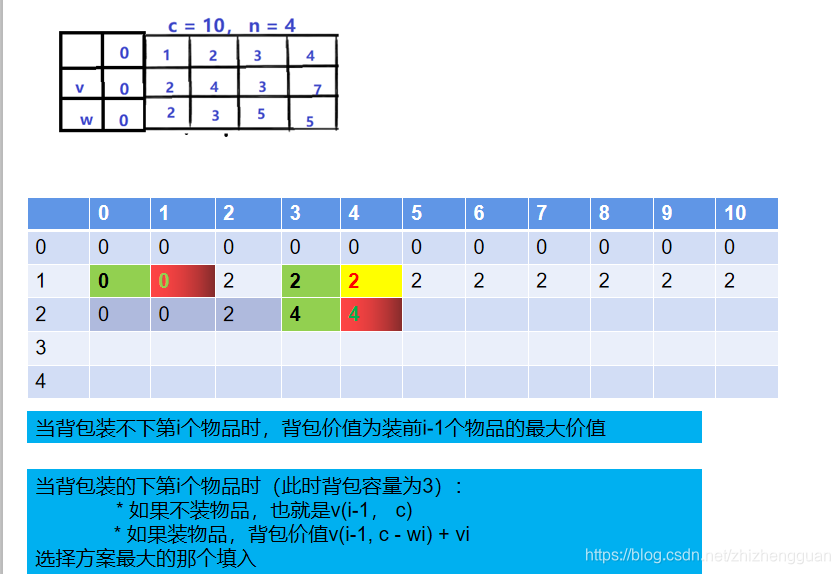
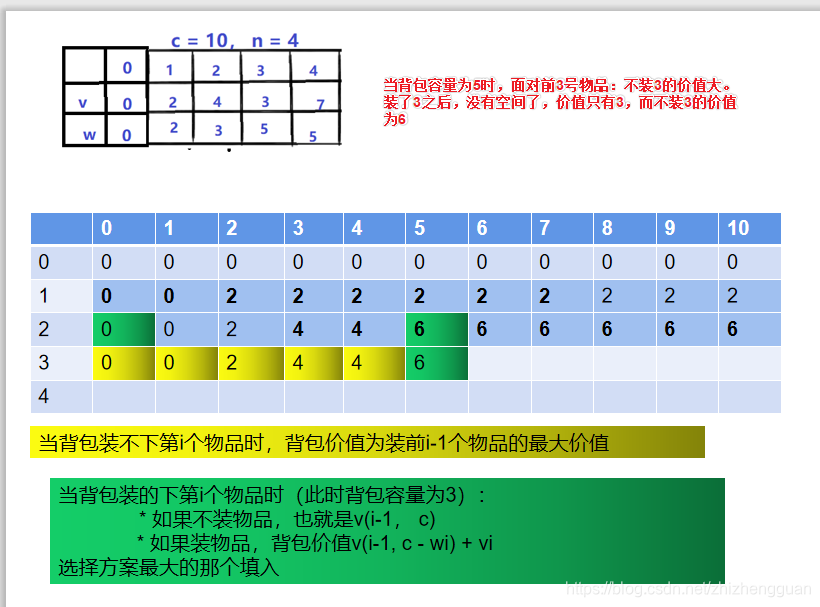
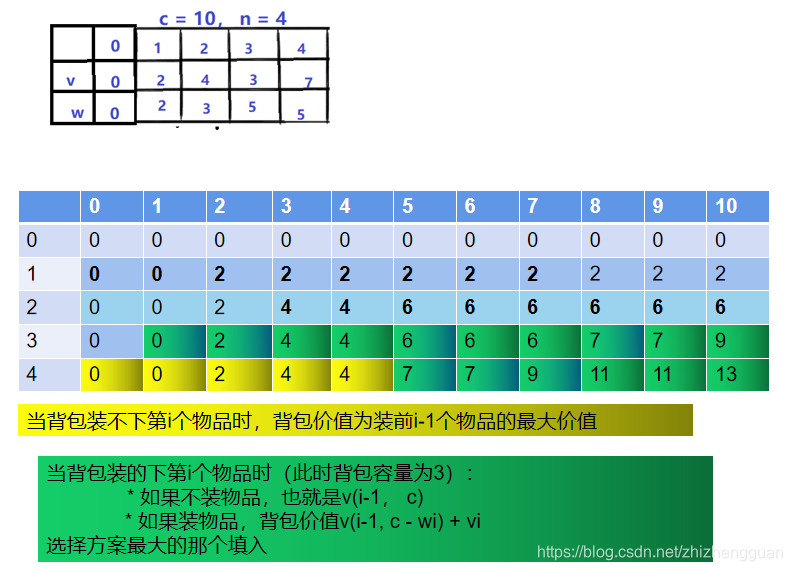
    在这里插入图片描述

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
*----
在这里插入图片描述

  • 当面对第3号物品时，背包剩余容量可能是0、1、2、。。。。10，装入之后背包的价值如下:【此时表格第3行就是装1、2、3得到的最大值】
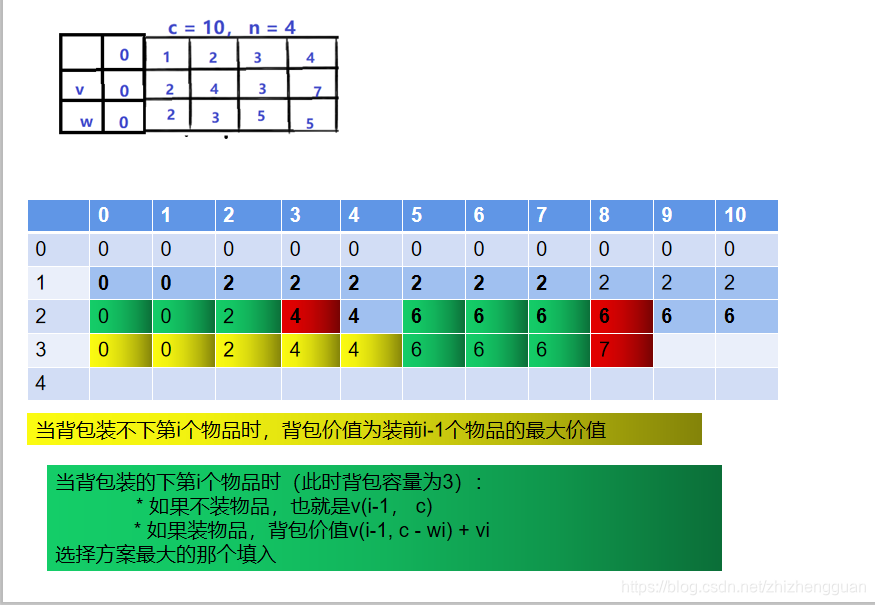
    在这里插入图片描述

在这里插入图片描述
在这里插入图片描述

  • 当面对前4个物品时，表格如下
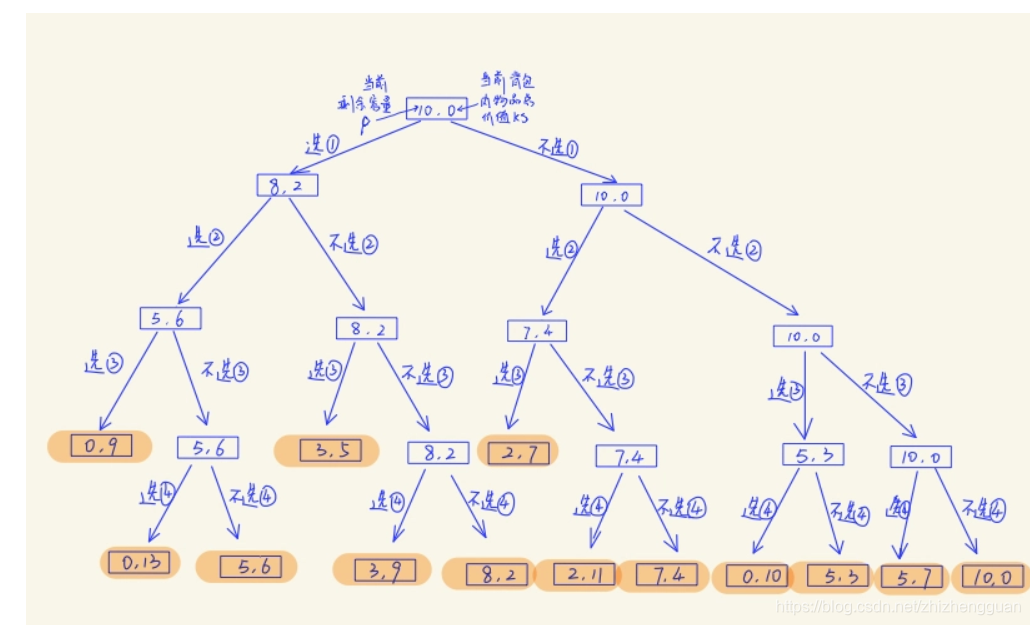
    在这里插入图片描述

0-1背包问题可以看成是二叉树的深度优先搜索

  • 假设有四个物品，它们的价值和体积如下图所示：
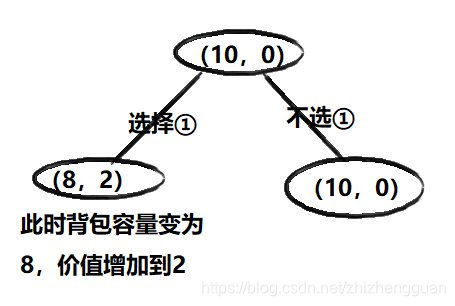
    在这里插入图片描述

初始时， 有F(10, 0)， 表示当前背包容量为10，当前背包里物品价值为0。

  • 那么对于物品1，他有两种决策：要 / 不要
    在这里插入图片描述
  • 对于背包容量2，有两种选择结果
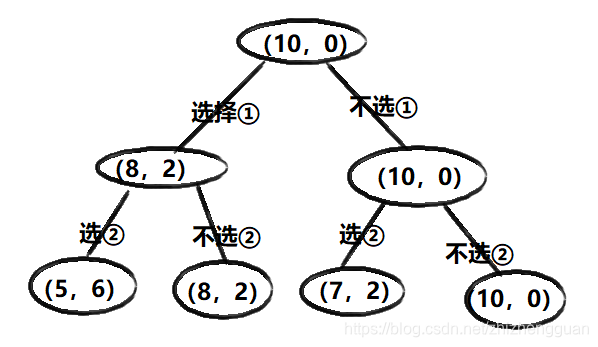
    在这里插入图片描述
    每做出一个选择，就会将上面的每一种可能分裂成两种可能，后续的选择也是如此，最终，我们会得到如下的一张决策图：
    在这里插入图片描述

然后，我们从这些结果中，找出价值最大的那个，也就是13，这就是我们的最优选择，根据这个选择，依次找到它的所有路径，便可以知道该选哪几个珠宝，最终结果是：4，2，1。

这个也可以看成是一颗二叉决策树的深度遍历

滚动数组

假设我们外层遍历物品，内层是背包容量。 假设我们是从左到右，从上到下遍历

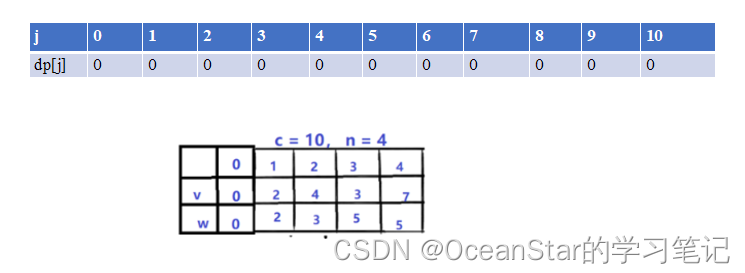
初始时：

在这里插入图片描述

装载第1个物品时，其重量是2，价值是2。

  • 【背包容量为0，可选物品1（重量2，价值2）】—》【物品1装不下，所以dp[0]为0】
  • 【背包容量为1，可选物品1（重量2，价值2）】—》【物品1装不下，此时背包容量为1，价值为0，所以dp[1]为0】
  • 【背包容量为2，可选物品1（重量2，价值2）】—》装得下，此时有两个选择（最优子结构有两个）：
    • 【背包容量为2，价值为0；可选物品1】—》【不装物品1，此时背包容量为2，价值为0】
    • 【背包容量为2，价值为0；可选物品1】—》【装物品1（价值2），此时背包容量变为0，背包的价值就是物品1的价值，为2】
    • 两个中选择一个最好的，因此选择方案2，背包的价值为2
  • 【背包容量为3，可选物品1（重量2，价值2）】—》装得下，此时有两个选择（最优子结构有两个）：
    • 【背包容量为3，价值为0；可选物品1】—》【不装物品1，此时背包容量为3，价值为0】
    • 【背包容量为3，价值为0；可选物品1】—》【装物品1（价值2），此时背包容量变为1，背包的价值就是物品1的价值，为2】–》【因为已经没有物品可以选择了，所以背包价值就是2】
    • 两个中选择一个最好的，因此选择装物品1，此时为2
  • 当背包容量为4时，装得下，价值是2
  • …

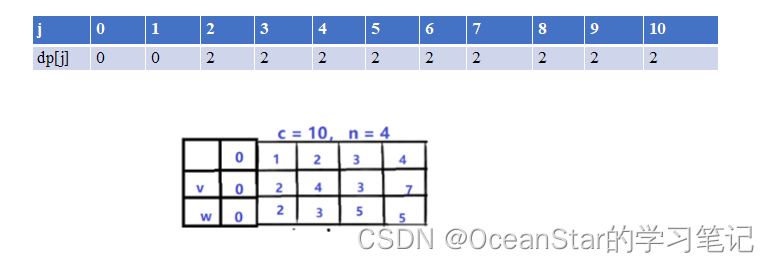
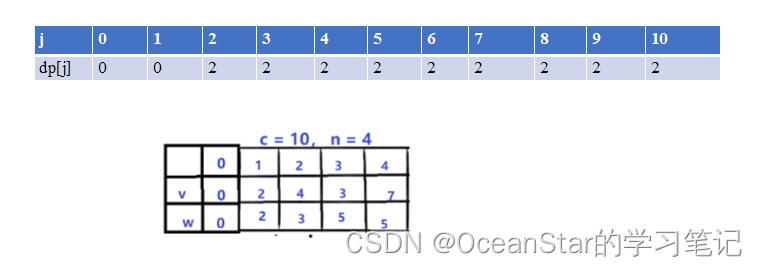
在这里插入图片描述
装载第2个物品时，其重量是3，价值是4。 dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);

  • 【背包容量为0，可选物品1（重量2，价值2），物品2（重量3，价值4）】.当前正在看物品2–》【物品2的重量超过了背包容量，一定不能装2，因此情况变为】–》【背包容量为0，可选物品1（重量2，价值2）；这个情况上面选过，为0】
  • 【背包容量为1，可选物品1（重量2，价值2），物品2（重量3，价值4）】.当前正在看物品2
    • 物品2的重量3超过了背包容量1，一定不能装2，因此情况变为【背包容量为1，可选物品1（重量2，价值2）】
    • ；这个情况上面选过，为0
  • …
  • 【背包容量为6，可选物品1（重量2，价值2），物品2（重量3，价值4）.当前正在看物品2】
    • 背包容量6大于物品2的重量3。因此可以选择装物品2和不装物品2
    • 假设我们选择装物品2，那么【背包容量变为了3】，而此时的dp[3]已经选择了物品2，如果value[2] + dp[3]，那就相当于物品2选择了两次

假设我们外层遍历物品，内层是背包容量。 假设我们是从右到左，从上到下遍历

  • 当给了物品1（重量2，价值2）时：

    • 背包容量为10时，可以装物品1
    • 背包容量为9时，可以装物品1
    • …
    • 背包容量为2时，可以装物品1
    • 背包容量为1时，不可以装物品1了

  • 当给了物品1（重量2，价值2），物品2（重量3，价值4）

    • 背包容量为10时，可以选择装物品2或者不装物品2
      • 不装物品2，此时背包中只装了物品1，因此价值是2
      • 装物品2，装了之后背包容量变为7，价值变为4—》容量为7的背包足够装下物品1，所以背包中【装物品1和物品2】，价值变为【价值2+价值4】 即【价值6】，此时背包还剩【5】
      • 两个方案中选择一个好的方案，最大价值变为6
    • 背包容量为9时，可以选择装物品2或者不装物品2
      • 同上，方案是【装物品1和物品2】最大价值是6
    • 背包容量为8时，可以选择装物品2或者不装物品2
      • 同上，方案是【装物品1和物品2】最大价值是6
    • 背包容量为7时，可以选择装物品2或者不装物品2
      • 同上，方案是【装物品1和物品2】最大价值是6
    • 背包容量为6时，可以选择装物品2或者不装物品2
      • 同上，方案是【装物品1和物品2】最大价值是6
    • 背包容量为5时，可以选择装物品2或者不装物品2
      • 同上，方案是【装物品1和物品2】最大价值是6，此时背包完全装满了
    • 背包容量为4时，不足以全部装载，只能选择装【物品1（重量2，价值2）】或者【物品2（重量3，价值4）】
      • 当不装物品2时，背包容量为4，价值为0，可以装下物品1，此时价值为2，背包容量还剩2
      • 当装物品2时，背包容量变为1，价值为4。容量1的空间不能装下物品1了，因此背包还剩为1
      • 所以我们应该装物品2而不是物品1，得到价值为4
    • 背包容量为3时，不足以全部装载，只能选择装【物品1（重量2，价值2）】或者【物品2（重量3，价值4）】选择一个价值大的装载，也就是装物品2但是不装物品1
    • 当背包容量为2时，只能装载【物品1】，此时背包价值为2
    • 当背包容量为1或者0时，什么也装不下，此时背包价值为0
      在这里插入图片描述
      在这里插入图片描述

  • 当给了物品1（重量2，价值2），物品2（重量3，价值4），物品3（重量3，价值5），面对物品3

    • 对于容量为10的背包，此时的dp[10]是面对【物品1、物品2】的最佳选择方案。此时需要加上物品3，因为容量为10的背包足以装下物品3，因此可以选择装或者不装
      • 不装，那么就相当于dp[10]对于【物品1、物品2】的最佳选择方案，价值为6
      • 装，dp[10] = 物品3的价值 + dp[10 - 物品3的重量] = 5 + dp[10 - 3] = 5 + dp[7]，当dp[7]时，就是面对[物品1、物品2]得到的最大收益为6，因此总的收益为 5 + 6 = 13
      • 两者选择一个最优的方案：13
    • …,…

假设我们外层遍历容量，内层是背包容量。 背包容量一定是倒序遍历。现在我们来选择物品

  • 对于容量为10的背包
    • 面对物品1，能放入，dp[10] = 物品1的价值
    • 面对物品2，能放入，dp[10] = 物品2的价值
    • 面对物品3，能放入，dp[10] = 物品3的价值
    • …
    • 只放了一个物品

所以一定要先遍历物品，在遍历背包，而且背包到倒序遍历
在这里插入图片描述

套路

动态规划无非就是状态+选择。所以，第一步，要明确两点：【状态】和【选择】

  • 先说状态，如何才能描述一个问题局面呢？只要给几个物品和一个背包的容量就形成了一个背包问题，所以状态有两个，就是[背包的容量] 和[可选择的物品]
  • 再说选择。想一想，针对每个物品，你能选择什么？选择无法就是[装]还是[不装]

明确了状态和选择，动态规划问题基本上就解决了一般，只要往下面这个框架里套就行了

for 状态1 in 状态1的所有取值：
	for 状态2 in 状态2的所有取值：
		for ...
			dp[状态1][状态2][...] = 择优(选择1，选择2...)

第二步：明确dp数组以及索引i的定义

  • 刚刚我们找的状态，有两个，因此我们需要一个二维数组dp[i][w]
  • 针对dp[i][w]：
    • 其定义如下：对于物品[0…i]，当前背包的容量为w，这种情况下可以装的最大价值是dp[i][w]
    • 举个例子：比如dp[3][5] = 6，含义为：对于给定的一系列物品中，如果只对物品num[0]、nums[1]、nums[2]、nums[3]进行选择，当背包容量为5时，最多可以装下的价值是6
  • 那么最终应该返回什么呢？dp[N][W]，也就是选择了N个物品，背包容量为W时的最大价值
  • dp数组如何初始化呢？base case 就是 dp[0][..] = dp[..][0] = 0 ，因为没有物品或者背包没有空间的时候，能装的最⼤价值就是 0。

细化上面的框架

int dp[N+1][W+1]
dp[0][..] = 0
dp[..][0] = 0

for i in [1..N]:
	for w in [1..W]:
		dp[i][w] = max(
			把物品 i 装进背包,
			不把物品 i 装进背包
		)

return dp[N][W]

第三步，根据「选择」，思考状态转移的逻辑。

  • 简单来说，就是上面伪代码中[把物品i装进背包]和[不把物品i装进背包]怎么用代码体现出来呢？这就要结合我们对dp数组的定义和我们的算法逻辑来分析了。

  • 先看我们对dp数组的定义：

    • dp[i][j]表示：对于物品[0…i]，当前背包容量为w时，能够装下的最大价值是dp[i][i]

  • 那么，对于第i个物品：

    • 如果没有把这第i个物品装入背包。那么很显然，最大价值dp[i][w] = dp[i - 1][w]。
      • dp[i][w]表示当物品[0…i]，容量为w时的最大价值
      • dp[i-1][w]表示当物品[0…i-1]，容量为w时的最大价值
    • 如果把第i个物品装入背包。那么最大价值 dp[i][w] =dp[i-1][w- wt[i]] + val[i]
      • dp[i][w]表示当物品[0…i]，容量为w时的最大价值
      • val[i]表示物品[i]的价值
      • dp[i-1][w- wt[i]]表示物品[0…i-1]，容量为w-wt[i]时的最大价值。也就是如果你装了第i个物品，就要去寻找剩下物品[0…i-1]，剩余重量w-wt[i]限制下的最大价值

  • 从上面，我们可以得出状态转移方程

for i in [1..N]:
	for w in [1..W]:
		dp[i][w] = max(
			dp[i-1][w],
			dp[i-1][w - wt[i]] + val[i]
		)
return dp[N][W]

最后⼀步，把伪码翻译成代码，处理⼀些边界情况。

class Solution {
public:
    void bag_problem(vector<int> weight, vector<int> value, int bagweight) {
        if(weight.empty() || bagweight == 0){
            return;
        }
        weight.insert(weight.begin(), 0);
        value.insert(value.begin(), 0);
        vector<vector<int>> dp(weight.size(), vector<int>(bagweight + 1, 0));


        int m = dp.size(), n = dp[0].size();
        for(int i = 1; i < m; i++) { // 遍历物品
            for(int j = 1; j < n; j++) { // 遍历背包容量
                if (j < weight[i]) {
                    dp[i][j] = dp[i - 1][j];
                }else {
                    dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
                }
            }
        }

        cout << dp[m - 1][n - 1] << endl;
    }
};

⾄此，背包问题就解决了

彻底理解0-1背包问题
背包问题9讲解
【动态规划】01背包问题（通俗易懂，超基础讲解）
【动态规划】01背包问题—》 推荐

悦读

道可道，非常道；名可名，非常名。 无名，天地之始，有名，万物之母。 故常无欲，以观其妙，常有欲，以观其徼。 此两者，同出而异名，同谓之玄，玄之又玄，众妙之门。

最新收录
java 程序、进程 、线程，cpu，并行、并发、启动线程两种方式
Anaconda+pycharm+pytorch安装教程（GPU版）
构建可扩展的JavaEE应用（一）
vxe-grid实现嵌套table，自实现联动多选
【word】文章里的表格边框是双杠
ES6面试、复习干货知识点汇总（全）
如何让 AI 交流更高效：明确目标与细化需求
【系统架构设计 每日一问】四 如何对关系型数据库及NoSql数据库选型
【全网最全】2024电工杯数学建模A题前两题完整解答matlab+21页初步参考论文+py代码等（后续会更新成品论文）
【动态带宽分配（DBA）通过IPACT在1G-EPON中的应用】IPACT（交错轮询自适应周期时间）是针对以太网无源光网络（EPON）的一种动态协议（Matlab代码实现）
;