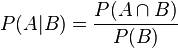朴素贝叶斯分类的优缺点及使用数据类型

一、作用

分类

二、基本原理

这篇文章，写的相当好。

从决策树学习谈到贝叶斯分类算法、EM、HMM：

http://blog.csdn.net/v_july_v/article/details/7577684

介绍算法基本思想前，先聊一下条件概率问题。看定义：http://zh.wikipedia.org/wiki/%E6%9D%A1%E4%BB%B6%E6%A6%82%E7%8E%87

在同一个样本空间Ω中的事件或者子集A与B，如果随机从Ω中选出的一个元素属于B，那么这个随机选择的元素还属于A的概率就定义为在B的前提下A的条件概率。从这个定义中，我们可以得出

P(A|B) = |A∩B|/|B|

分子、分母都除以|Ω|得到

有时候也称为：后验概率

贝叶斯公式：下面是对贝叶斯公式最好的解释：

图解贝叶斯公式:http://barrons.blog.caixin.com/archives/54496

 贝叶斯公式推导

P(A/B) = P(A*B)/P(B), P(A*B) = P(A/B)*P(B)

P(B/A) = P(A*B)/P(A), P(A*B) = P(B/A)*P(A)

P(A/B)*P(B) = P(B/A)*P(A) , P(A/B) = P(B/A)*P(A)/P(B) 

朴素贝叶斯分类器的公式

引自：http://www.ruanyifeng.com/blog/2013/12/naive_bayes_classifier.html

假设某个体有n项特征（Feature），分别为F₁、F₂、...、F_n。现有m个类别（Category），分别为C₁、C₂、...、C_m。贝叶斯分类器就是计算出概率最大的那个分类，也就是求下面这个算式的最大值：

　P(C|F1F2...Fn) 
　　= P(F1F2...Fn|C)P(C) / P(F1F2...Fn)

由于 P(F1F2...Fn) 对于所有的类别都是相同的，可以省略，问题就变成了求

　P(F1F2...Fn|C)P(C)

的最大值。

朴素贝叶斯分类器则是更进一步，假设所有特征都彼此独立，因此

　P(F1F2...Fn|C)P(C) 
　　= P(F1|C)P(F2|C) ... P(Fn|C)P(C)

上式等号右边的每一项，都可以从统计资料中得到，由此就可以计算出每个类别对应的概率，从而找出最大概率的那个类。

虽然"所有特征彼此独立"这个假设，在现实中不太可能成立，但是它可以大大简化计算，而且有研究表明对分类结果的准确性影响不大。

下面再通过两个例子，来看如何使用朴素贝叶斯分类器。

三、应用：

1、使用朴素贝叶斯分类器过滤垃圾邮件

 贝叶斯推断及其互联网应用（二）：过滤垃圾邮件 ：http://blog.chinaunix.net/uid-26548237-id-3853480.html

(1) 建立过滤器

 贝叶斯过滤器是一种统计学过滤器，建立在已有的统计结果之上。所以，我们必须预先提供两组已经识别好的邮件，一组是正常邮件，另一组是垃圾邮件。
    我们用这两组邮件，对过滤器进行“训练”。这两组邮件的规模越大，训练效果就越好。Paul Graham使用的邮件规模，是正常邮件和垃圾邮件各4000封。
    “训练”过程很简单。首先，解析所有的邮件，提取每一个词。然后，计算每个词语在正常邮件和垃圾邮件中出现的频率。比如，我们假定“sex”这个词，在4000封垃圾邮件中，有200封包含这个词，那么它的出现频率就是5%；而在4000封正常邮件中，只有2封包含这个词，那么出现频率就是0.05%。（【注释】如果某个词   只出现   在垃圾邮件中，Paul Graham就假定，它在正常邮件的出现频率是1%（经验值，可以根据新收的邮件不断调整），反之亦然。这样做是为了避免概率为0。随着邮件数量的增多，计算结果会自动调整。）
    有了这个初步的统计结果，过滤器就可以投入使用了。

(2) 分类

1）统计出待检测邮件中词频最高的10来个词（当然也不一定是10来个，视具体情况而定）；

2）分别在样本S（Spam）和H（Health）集中，统计这10来个词的出现概率P（Fi/H），P（Fi/S）。

3）假设出现H和S的概率为50%，则比较下列两个值，取概率大者。

  P(F1|H)P(F2|H) ... P(Fn|H)P(H)

  P(F1|S)P(F2|S) ... P(Fn|S)P(S)

结束！

2使用朴素贝叶斯分类器过滤网站恶意留言