1.递归的定义
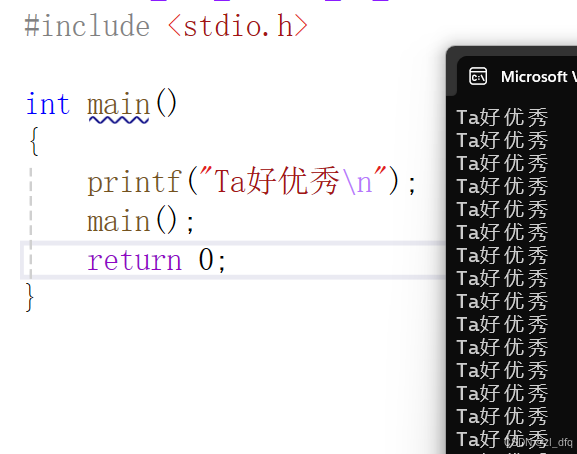
在C语言中,递归就是函数自己调用自己
上面的代码就是 main 函数在函数主体内 自己调用自己
但是,上面的代码存在问题:main 函数反复地 自己调用自己 ,不受限制,停不下来。
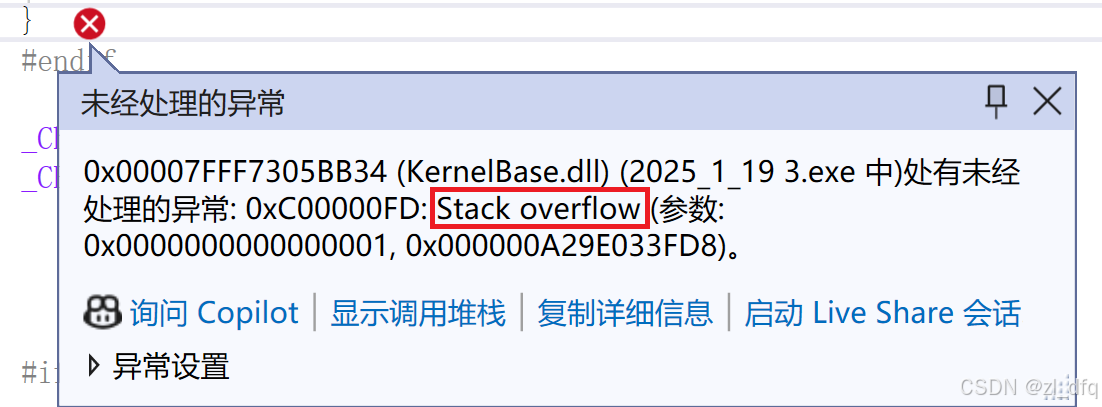
最终形成死递归,导致栈溢出
1.0栈溢出
每一次函数调用,都要从内存上的栈区为这次函数调用分配内存空间
栈区的大小是有限的,如果无限的调用函数就会导致栈区空间被使用完,
从而发生栈溢出的现象,导致程序运行停止
1.1递归的思想
将一个大问题细分为一个个子问题,直到子问题不可拆分为止就是递归的思想。
递归就是将大事化小的过程。
递,就是递推;归,就是回归。
1.2.递归的书写条件
(1)递归存在限制条件,当条件满足时,递归便不再继续
(2)每次递归调用之后,越来越接近这个限制条件
2.举例
2.1阶乘
我们知道,n! = n * (n-1) * (n-2) * (n-3) * ……* 2 * 1
又注意到,2! = 2 * 1! || 3! = 3 * 2! || 4! = 4 * 3!
所以 n! = n * (n -1)!
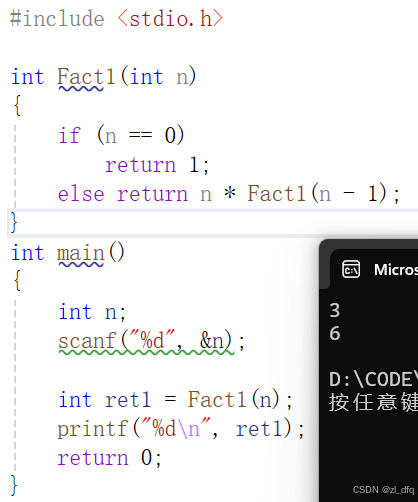
int Fact1(int n)
{
if (n == 0)
return 1;
else return n * Fact1(n - 1);
}当 n = 3 时
Fact1(3) = 3*Fact1(2)
Fact1(2) = 2*Fact1(1)
Fact1(1) = 1*Fact1(0)
Fact1(0) = 1
先是递推,每次函数调用之后,接近 n 等于 0 这个限制条件
然后回归
Fact1(0) = 1
Fact1(1) = 1*Fact1(0) = 1
Fact1(2) = 2*Fact1(1) = 2
Fact1(3) = 3*Fact1(2) = 6
2.2顺序打印整数的每一位
运用递归时,我们要相信我们所创建的函数能够完成相应的任务
例如,顺序打印 123 中的每一位
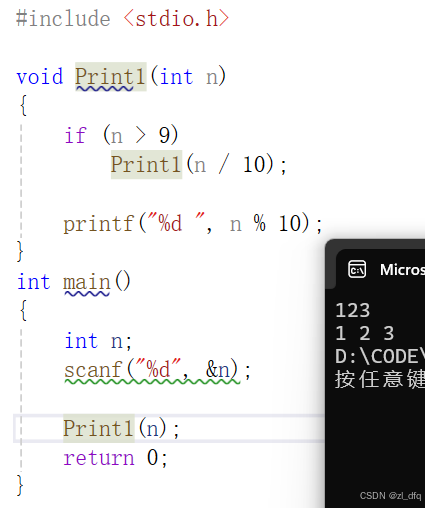
void Print1(int n)
{
if (n > 9)
Print1(n / 10);
printf("%d ", n % 10);
}
在上面的代码实现中:
Print(123)中 123 > 9 所以 先调用函数Print(123/10)打印 12 再打印3
Print(123 / 10)中 12 > 9 所以 先调用函数Print(12/10)打印 1 再打印2,
Print(12 / 10)中 1 < 9 开始 打印 1,函数Print(12 / 10)调用完毕
然后返回函数Print(123 / 10)打印 2, 再返回函数Print(123)打印3
Print(123) -> Print(123 / 10) -> Print(12 / 10)
这是递推, 将 大问题转化位 小问题, 只打印个位数
Print(12 / 10) - > Print(123 / 10) -> Print(123)
这是回归 ,因为只有函数调用任务实现后,才会继续后面的操作
2.3斐波那契数列
1,1,2,3,5,8,13,21,34........
第一二个数为1,其余的数等于前两个数相加,就是斐波那契数列的规律
代码实现:
int Fib(int n)
{
if (n < 3)
return 1;
else return Fib(n - 1) + Fib(n - 2);
}例如 n = 4
Fib(4) = Fib(3) + Fib(2)
Fib(3) = Fib(2) + Fib(1)
Fib(2) = 1
这是递推,然后回归
Fib(3) = 1 +Fib(1)
Fib(1) = 1
所以Fib(3) = 1+ 1 = 2
继续回归
Fib(4) = 2 + Fib(2)
Fib(2) = 1
Fib(4) = 2 +1 = 3
注意:只用当前一个Fib函数调用完毕后才会调用后面的Fib函数
3.递归与迭代
上述例子用递归的思想实现时,代码较为简洁
但不可避免的是,如果递归的层次太深,栈溢出的现象就不可避免
所谓层次太深,就是说许多函数被调用后,未被销毁,依然占据着栈区的部分内存
最终导致栈区空间被使用完,出现栈溢出的现象
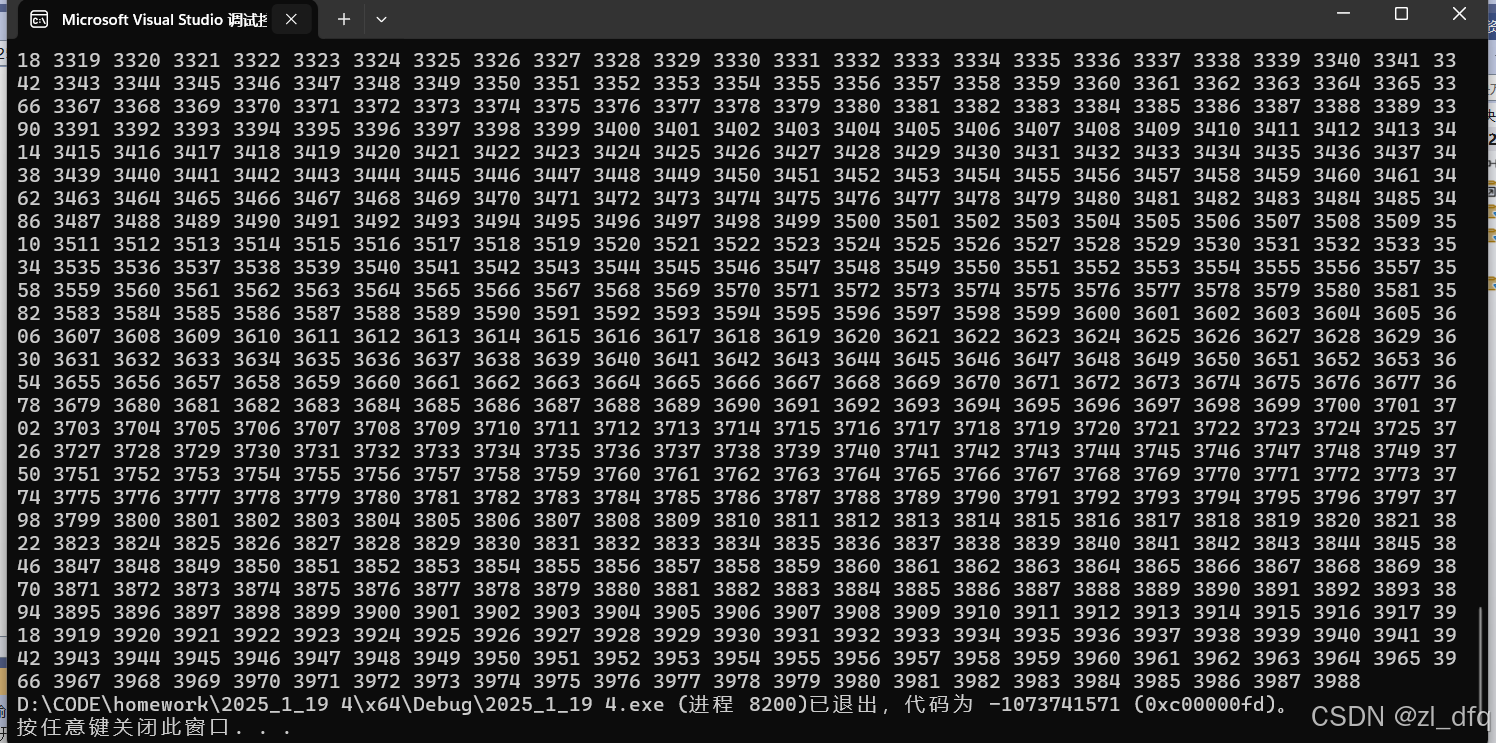
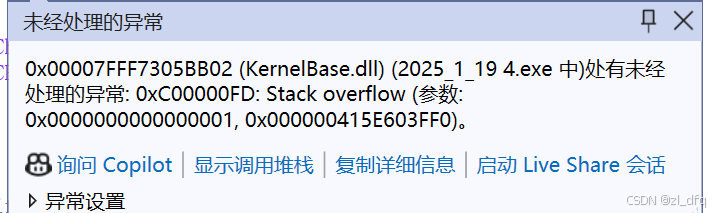
虽然存在限制条件 n > 10000 但是 3988次调用之后,程序就自动停止了 ,
因为递归层次太深,出现了栈溢出的现象
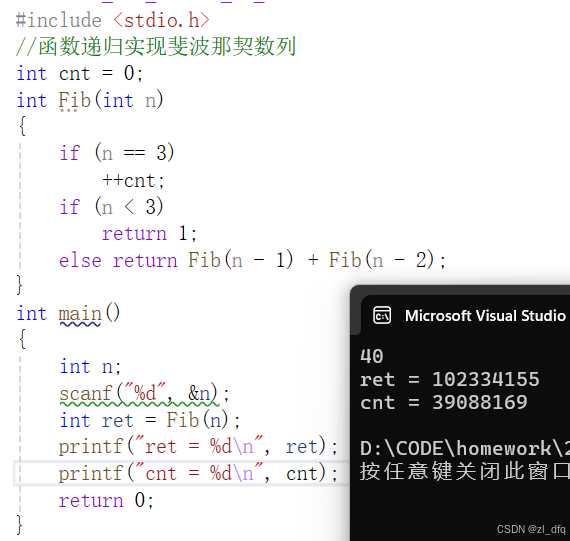
注意到,Fib函数虽然被调用了很多次,但是却没有出现栈溢出的现象
这是因为Fib(40)最深只会调用40次,然后就会被销毁,再继续后面的调用
..........................................................................................................................................
注意到,Fib(40)重复调用的Fib函数太多,运行效率非常低
此时就可以采用迭代的方法实现斐波那契数列。
循环是一种迭代,迭代不仅仅是循环
int Fact2(int n)
{
int a = 1;//前两个数
int b = 1;//前一个数
int c = 1;//当前的数
//当n 小于等于 2时
//直接返回c 为 1
//当n 大于 2时
//1 + 1 = 2 1+ 2 = 3 2+ 3 = 5
//第n个数需要迭代n-2次
for (int i = 0; i < n - 2; ++i)
{
c = a + b;
a = b;
b = c;
}
return c;
}运行一下就知道,迭代实现斐波那契数列比递归更快!
但是解决实际问题时
递归比较好想,如果能保证不会出现栈溢出等问题就可优先考虑使用递归
其次是迭代