系列文章目录及链接

上篇：机器学习（五） -- 无监督学习（1） --聚类1
下篇：

前言

tips：标题前有“***”的内容为补充内容，是给好奇心重的宝宝看的，可自行跳过。文章内容被“文章内容”删除线标记的，也可以自行跳过。“！！！”一般需要特别注意或者容易出错的地方。

本系列文章是作者边学习边总结的，内容有不对的地方还请多多指正，同时本系列文章会不断完善，每篇文章不定时会有修改。

由于作者时间不算富裕，有些内容的《算法实现》部分暂未完善，以后有时间再来补充。见谅！

文中为方便理解，会将接口在用到的时候才导入，实际中应在文件开始统一导入。

 三、**算法实现

四、接口实现

1、K-means

1.1、API

sklearn.cluster.KMeans
 
导入：
from sklearn.cluster import KMeans
 
语法：
KMeans(n_clusters=8,init=‘k-means++’,n_init='warn', max_iter=300, tol=0.0001, verbose=0, random_state=None, copy_x=True, algorithm='lloyd')
参数：
    n_clusters:开始的聚类中心数量，默认=8，
    init:初始化方法，默认为‘k-means ++

属性：
KMeans.cluster_centers_：簇中心的坐标
KMeans.labels_：每个样本的标签

方法：
KMeans.fit(x)
KMeans.predict(x)
KMeans.fit_predict(x)
    计算聚类中心并预测每个样本属于哪个类别,相当于先调用fit(x),然后再调用predict(x)

1.2、流程

1.2.1、获取数据

from sklearn.datasets import load_iris

from sklearn.cluster import KMeans

# 获取数据
iris = load_iris()

1.2.2、数据预处理

# 划分数据集
x=iris.data
y=iris.target

1.2.3、特征工程

1.2.4、模型训练

# 实例化学习器
kmeans = KMeans(n_clusters=3, random_state=1473, n_init='auto')

# 模型训练
kmeans.fit(x)

1.2.5、模型评估

# 用模型计算测试值，得到预测值
y_pre = kmeans.predict(x)

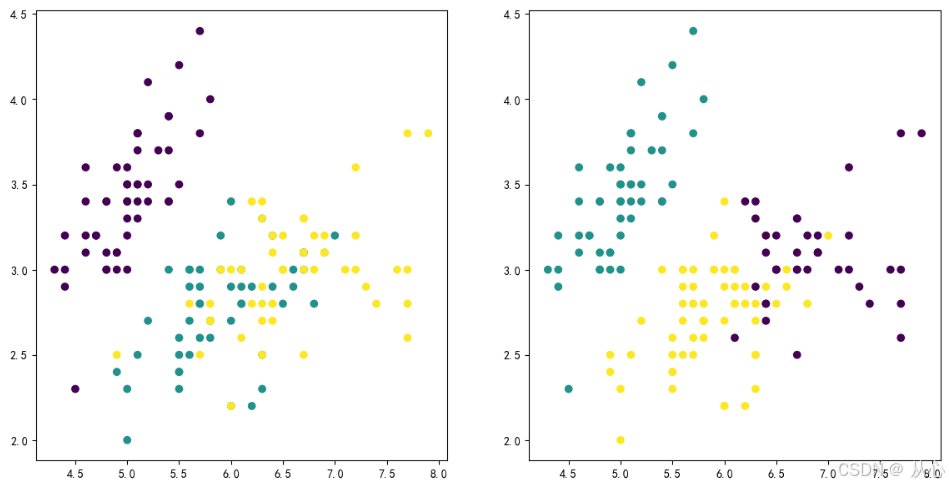
# 可视化
plt.figure(figsize=(14,7))
plt.subplot(121)
# 绘制iris原本的类别
plt.scatter(x[:, 0], x[:, 1], c=y)

plt.subplot(122)
# 绘制kmeans聚类结果
plt.scatter(x[:, 0], x[:, 1], c=y_pre)
plt.show()

from sklearn.metrics import jaccard_score, fowlkes_mallows_score, adjusted_rand_score, davies_bouldin_score
print('K均值聚类模型的Jaccard系数：', jaccard_score(y, y_pre,average='micro'))
print('K均值聚类模型的FM系数：', fowlkes_mallows_score(y, y_pre))
print('K均值聚类模型的调整Rand指数：', adjusted_rand_score(y, y_pre))
print('K均值聚类模型的DB指数：', davies_bouldin_score(x, kmeans.labels_))

1.2.6、结果预测

经过模型评估后通过的模型可以代入真实值进行预测。

2、K-Medoids

make_blobs的API：

        生成聚类数据集

sklearn.datasets.make_blobs

导入：
from sklearn.datasets import make_blobs

方法：
x, y = make_blobs(n_samples=1000, 
                  n_features=2, 
                  centers=[[-1, -1], [0, 0], [1, 1], [2, 2]],
                  cluster_std=[0.4, 0.2, 0.2, 0.2],
                  random_state=1473)
    x为样本特征，y为样本簇类别
    n_samples：样本数，默认=100；
    n_features：样本特征数（样本维度），默认=2；
    centers：族中心个数，可以是数字，也可以是点坐标，默认=3；
    cluster_std：簇标准差，默认=10；

2.1、获取数据

from sklearn.datasets import make_blobs

# 获取数据
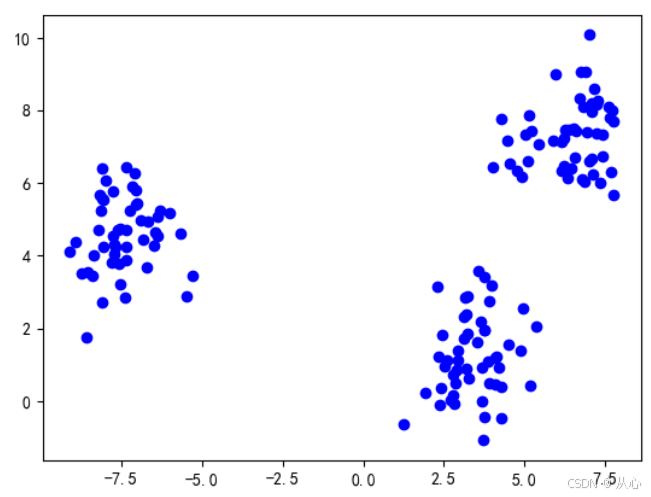
x,y = make_blobs(n_samples=150, centers=3, n_features=2, random_state=1734)

# 可视化
plt.figure()
plt.scatter(x[:, 0], x[:, 1], c='b')
plt.show()

2.2、数据预处理

2.3、特征工程

2.4、模型训练

class KMedoids1:
    def __init__(self,k=3,max_iter=100):
        self.k = k
        self.max_iter = max_iter

    def euclidean_distance(self, x1, x2):
        return np.sqrt(np. sum( (x1 - x2) **2))

    def fit(self, X):
        n_samples,n_features = X.shape

        #初始化聚类中心,从样本点中随机选取k个点作为聚类中心
        centers = np.sort(np.random.choice(n_samples,self.k,replace=False))
        medoids = X[centers]

        for i in range(self.max_iter) :
            #计算每个样本点到每个聚类中心之间的距离
            distances = np.zeros((n_samples,self.k))
            for j in range(self.k):
                distances[:,j] = np.apply_along_axis(self.euclidean_distance,1,X,medoids[j])

            #找到距离每个聚类中心最近的点，作为新的聚类中心
            closest_centroid = np.argmin(distances,axis=1)
            for j in range(self.k):
                medoids[j] = np.median( X[closest_centroid == j],axis=0)

        self.medoids = medoids
        self.labels = closest_centroid
        return self

kmedoids=KMedoids1(3)
kmedoids.fit(x)

2.5、模型评估

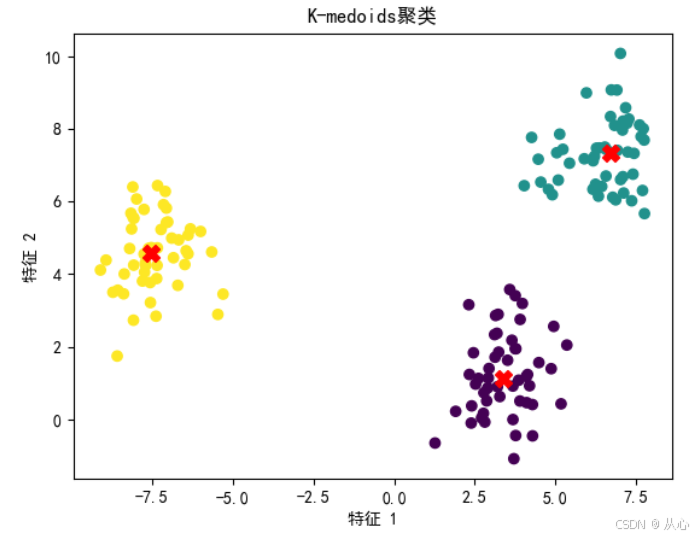
plt.figure()
plt.scatter(x[:, 0], x[:, 1], c=kmedoids.labels, cmap='viridis', marker='o', label='Data points')
plt.scatter(kmedoids.medoids[:,0],kmedoids.medoids[:,1], c='red', marker='X', s=100, label='Medoids')
plt.title('K-medoids聚类')
plt.xlabel('特征 1')
plt.ylabel('特征 2')
plt.show()

2.6、结果预测

经过模型评估后通过的模型可以代入真实值进行预测。

3、层次聚类--AGNES

2.1、API

sklearn.cluster.AgglomerativeClustering
 
导入：
from sklearn.cluster import AgglomerativeClustering
 
语法：
AgglomerativeClustering(n_clusters=2, *, affinity='euclidean', memory=None, connectivity=None, compute_full_tree='auto', linkage='ward', distance_threshold=None)
参数：
    n_clusters：指定聚类的簇数。
    affinity：指定距离度量的方式，可以是预定义的
            （如"euclidean"、"l1"、"l2"、"manhattan"等）或者自定义的距离度量函数。
    linkage：指定连接方式，用于计算两个簇之间的距离，可以是预定义的字符串
            （如" single"、"ward"、"complete"、"average"等）或者自定义的连接函数。
    connectivity：指定连接矩阵，用于限制哪些样本可以连接到一起的布尔数组或可调用对象。
    compute_full_tree：指定是否计算完整的层次聚类树。
    distance_threshold：指定停止合并簇的距离阈值。
    memory：指定内存缓存的路径，以便加速计算。
    compute_distances：指定是否在计算连接矩阵时计算距离矩阵。


属性：


方法：

2.2、流程

2.2.1、获取数据

from scipy.cluster.hierarchy import linkage          #导入linage函数用于层次聚类
from scipy.cluster.hierarchy import dendrogram       #dendrogram函数用于将聚类结果绘制成树状图
from scipy.cluster.hierarchy import fcluster         #fcluster函数用于提取出聚类的结果
from sklearn.datasets import make_blobs              #make_blobs用于生成聚类算法的测试数据
from sklearn.cluster import AgglomerativeClustering  #自底向上层次聚类算法

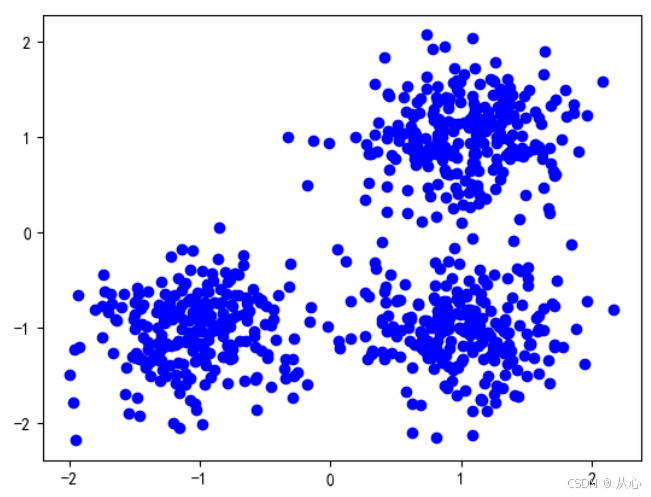
# 获取数据
centers = [[1, 1], [-1, -1], [1, -1]]
X, labels_true = make_blobs(n_samples=750, centers=centers, cluster_std=0.4, random_state=1473)

# 可视化
plt.figure()
plt.scatter(X[:, 0], X[:, 1], c='b')
plt.show()

2.2.2、数据预处理

2.2.3、特征工程

2.2.4、模型训练

#层次聚类实现
Z = linkage(X,  method='ward', metric='euclidean')
print(Z.shape)
print(Z[: 5])

2.2.5、模型评估

# 用模型计算测试值，得到预测值


# 
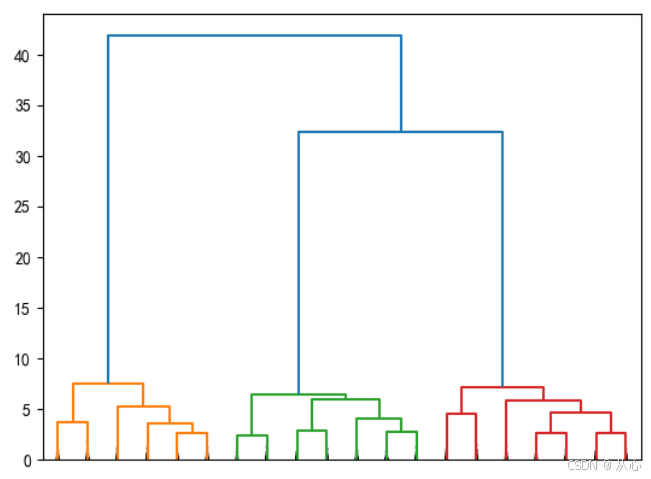
#画出树状图
plt.figure()
dendrogram(Z, truncate_mode='lastp', p=20, show_leaf_counts=False, leaf_rotation=90, leaf_font_size=15,
           show_contracted=True)
plt.show()

#根据临界距离返回聚类结果
d = 15
labels_1 = fcluster(Z, t=d, criterion='distance')
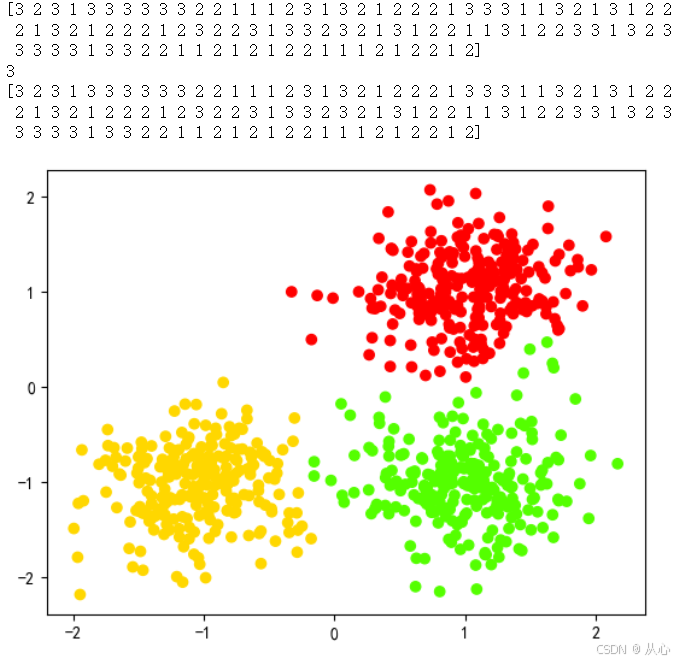
print(labels_1[: 100])  # 打印聚类结果
print(len(set(labels_1)))  # 看看在该临界距离下有几个 cluster

#根据聚类数目返回聚类结果
k = 3
labels_2 = fcluster(Z, t=k, criterion='maxclust')
print(labels_2[: 100])
list(labels_1) == list(labels_2)  # 看看两种不同维度下得到的聚类结果是否一致

#聚类的结果可视化，相同的类的样本点用同一种颜色表示
plt.figure()
plt.scatter(X[:, 0], X[:, 1], c=labels_2, cmap='prism')
plt.show()

2.2.6、结果预测

经过模型评估后通过的模型可以代入真实值进行预测。

2.2.7、对比不同方法聚类效果

from time import time
import numpy as np
from sklearn.datasets import make_blobs
from scipy.cluster.hierarchy import linkage, fcluster
from sklearn.metrics.cluster import adjusted_mutual_info_score
import matplotlib.pyplot as plt

#生成样本点
centers = [[1, 1], [-1, -1], [1, -1]]
X, labels = make_blobs(n_samples=750, centers=centers,
                       cluster_std=0.4, random_state=0)


#可视化聚类结果
def plot_clustering(X, labels, title=None):
    plt.scatter(X[:, 0], X[:, 1], c=labels, cmap='prism')
    if title is not None:
        plt.title(title, size=17)
    plt.axis('off')
    plt.tight_layout()

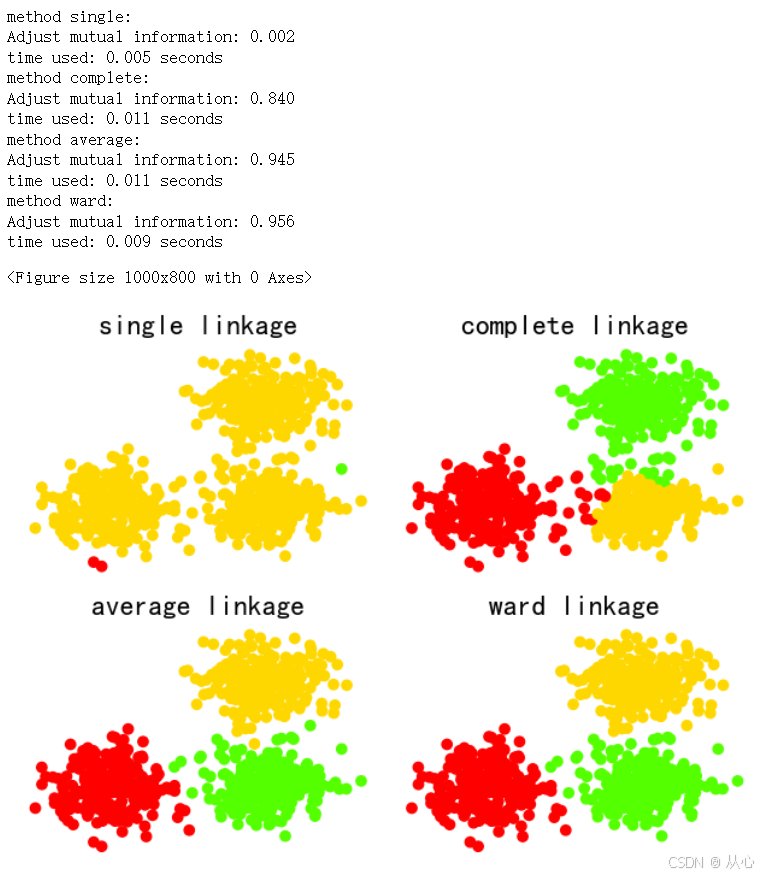
#进行 Agglomerative 层次聚类
linkage_method_list = ['single', 'complete', 'average', 'ward']

plt.figure(figsize=(10, 8))
ncols, nrows = 2, int(np.ceil(len(linkage_method_list) / 2))
plt.subplots(nrows=nrows, ncols=ncols)
for i, linkage_method in enumerate(linkage_method_list):
    print('method %s:' % linkage_method)
    start_time = time()
    Z = linkage(X, method=linkage_method)
    labels_pred = fcluster(Z, t=3, criterion='maxclust')
    print('Adjust mutual information: %.3f' % adjusted_mutual_info_score(labels, labels_pred))
    print('time used: %.3f seconds' % (time() - start_time))
    plt.subplot(nrows, ncols, i + 1)
    plot_clustering(X, labels_pred, '%s linkage' % linkage_method)
plt.show()

4、密度聚类--DBSCAN

4.1、API

sklearn.cluster.DBSCAN
 
导入：
from sklearn.cluster import DBSCAN
 
语法：
DBSCAN(eps=0.5, min_samples=5, metric='euclidean', algorithm='auto', leaf_size=30, p=None, n_jobs=1)
参数：
    eps:两个样本之间的最大距离，即扫描半径
    min_samples ：作为核心点的话邻域(即以其为圆心，eps为半径的圆，含圆上的点)中的最小样本数(包括点本身)。
    metric ：度量方式，默认为欧式距离，还有metric=‘precomputed’（稀疏半径邻域图）
    algorithm：近邻算法求解方式，有四种：‘auto’, ‘ball_tree’, ‘kd_tree’, ‘brute’
    leaf_size：叶的大小，在使用BallTree or cKDTree近邻算法时候会需要这个参数
    n_jobs ：使用CPU格式，-1代表全开


属性：
DBSCAN.core_sample_indices_:核心样本指数。（此参数在代码中有详细的解释）
DBSCAN.labels_:数据集中每个点的集合标签给,噪声点标签为-1。
DBSCAN.components_ ：核心样本的副本

方法：
DBSCAN.fit(x)
DBSCAN.predict(x)
DBSCAN.fit_predict(x)
    计算聚类中心并预测每个样本属于哪个类别,相当于先调用fit(x),然后再调用predict(x)

 make_circles的API：

生成数据集，形成一个二维的大圆，包含一个小圆

sklearn.datasets.make_circles

导入：
from sklearn.datasets import make_circles

方法：
x, y = make_circles(n_samples=5000, factor=.6, noise=.05, random_state=1473)
    x为样本特征，y为样本簇类别
    n_samples：样本数，默认=100；
    factor：0 < double <1 默认值0.8，内外圆之间的比例因子
    noise：设置噪声,小的话比较集中

4.2、流程

4.2.1、获取数据

from sklearn import datasets
from sklearn.cluster import DBSCAN

# 获取数据
# 生成两簇非凸数据
x1, y2 = make_blobs(n_samples=1000, n_features=2,
                             centers=[[1.2, 1.2]], cluster_std=[[.1]],
                             random_state=9)

# 一簇对比数据
x2, y1 = datasets.make_circles(n_samples=5000, factor=.6, noise=.05)
x = np.concatenate((x1, x2))
plt.scatter(x[:, 0], x[:, 1], marker='o')
plt.show()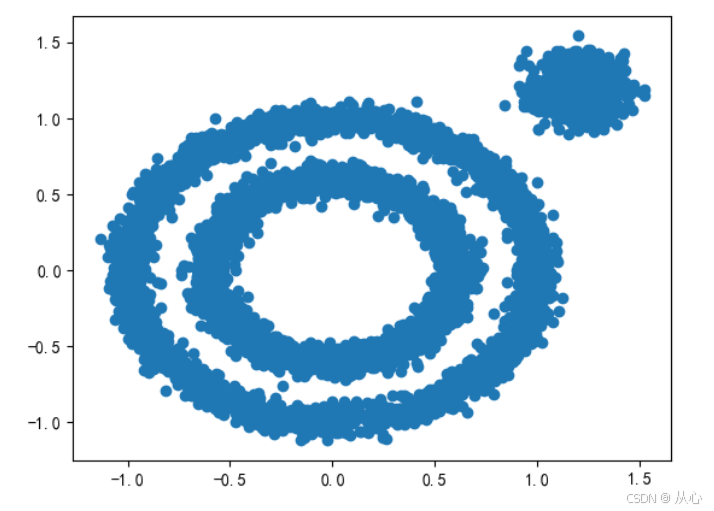

4.2.2、数据预处理

4.2.3、特征工程

4.2.4、模型训练

# 实例化学习器
dbs = DBSCAN(eps=0.1, min_samples=12).fit(x)
print('DBSCAN模型:\n', dbs)

# 模型训练+预测
ds_pre = dbs.fit_predict(x)

4.2.5、模型评估

# 用模型计算测试值，得到预测值


# 
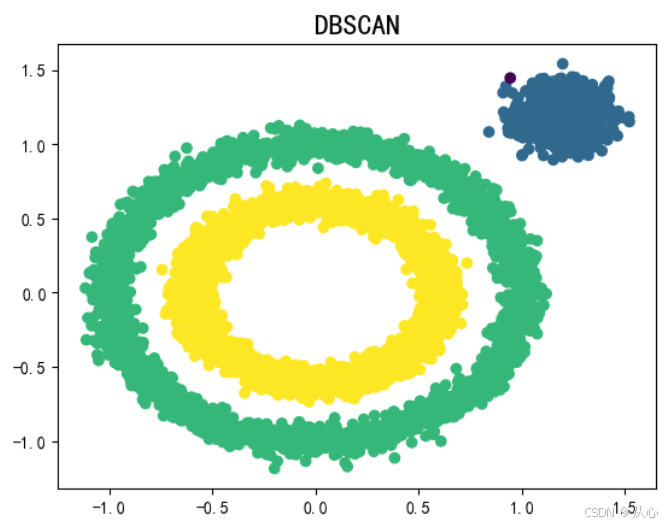
# 绘制DBSCAN模型聚类结果
plt.scatter(x[:, 0], x[:, 1], c=ds_pre)
plt.title('DBSCAN', size=17)
plt.show()

4.2.6、结果预测

经过模型评估后通过的模型可以代入真实值进行预测。

5、高斯混合模型（GMM）

5.1、API

sklearn.cluster.KMeans
 
导入：
from sklearn.cluster import KMeans
 
语法：
KMeans(n_clusters=8,init=‘k-means++’)
    n_clusters:开始的聚类中心数量
    init:初始化方法，默认为'k-means ++’
    labels_:默认标记的类型，可以和真实值比较（不是值比较）

5.2、流程

5.2.1、获取数据

# API导入
from sklearn.mixture import GaussianMixture

# 获取数据
# 生成模拟数据
X, _ = make_blobs(n_samples=300, centers=4, cluster_std=0.60, random_state=0)

5.2.2、数据预处理

5.2.3、特征工程

5.2.4、模型训练

# 实例化学习器
gmm = GaussianMixture(n_components=4)


# 模型训练
gmm.fit(X)

5.2.5、模型评估

# 预测测试集结果
clusters = gmm.predict(X)


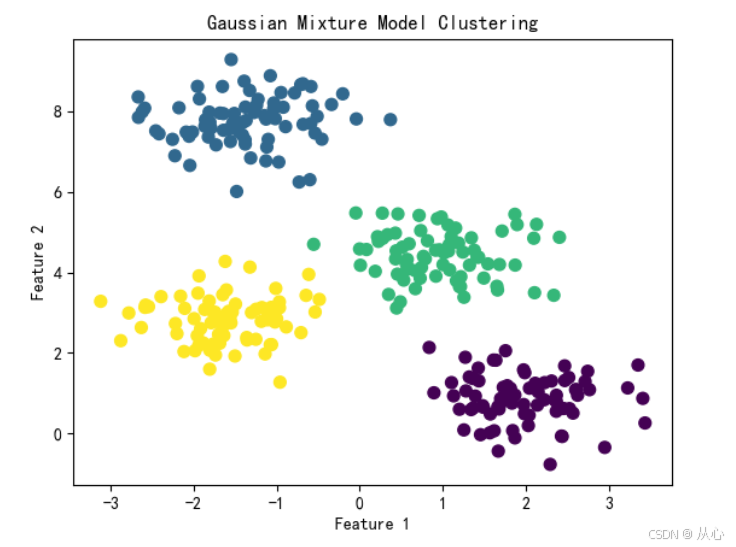
# 可视化
plt.scatter(X[:, 0], X[:, 1], c=clusters, cmap='viridis', marker='o', s=50)
plt.title("Gaussian Mixture Model Clustering")
plt.xlabel("Feature 1")
plt.ylabel("Feature 2")
plt.show()

5.2.6、结果预测

经过模型评估后通过的模型可以代入真实值进行预测。

旧梦可以重温，且看：机器学习（五） -- 无监督学习（1） --聚类1
欲知后事如何，且看：