http://www.yyycode.cn/index.php/2020/05/16/%e7%a7%91%e5%a4%a7%e8%ae%af%e9%a3%9e%e6%9d%af%e7%ac%ac%e5%8d%81%e4%b8%83%e5%b1%8a%e5%90%8c%e6%b5%8e%e5%a4%a7%e5%ad%a6%e7%a8%8b%e5%ba%8f%e8%ae%be%e8%ae%a1%e9%a2%84%e9%80%89%e8%b5%9b/ 

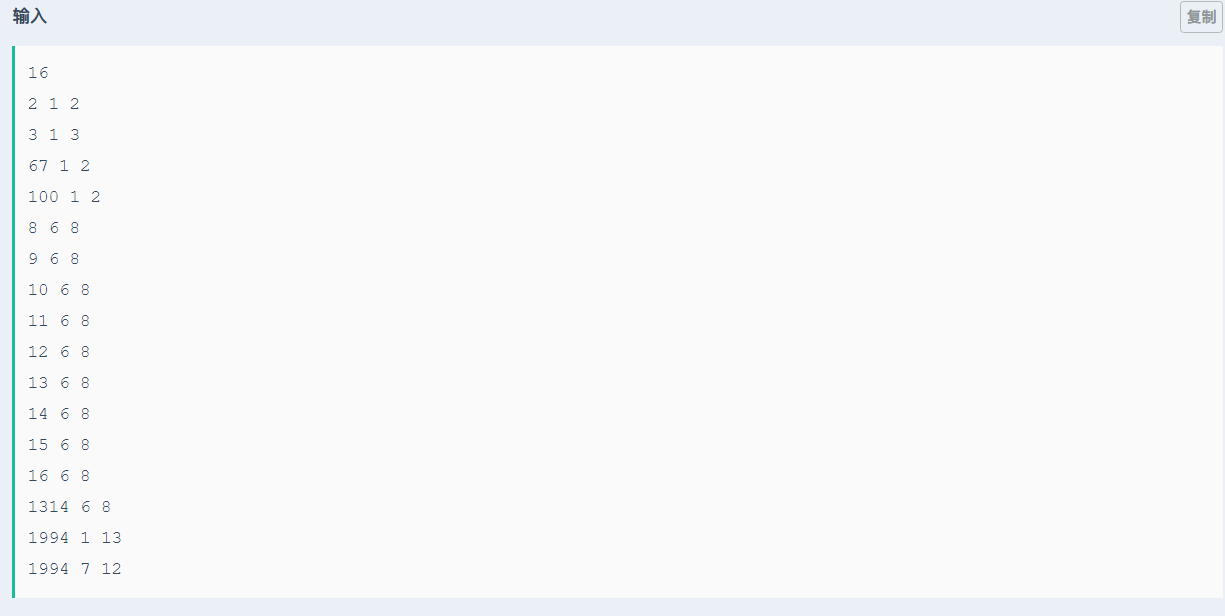
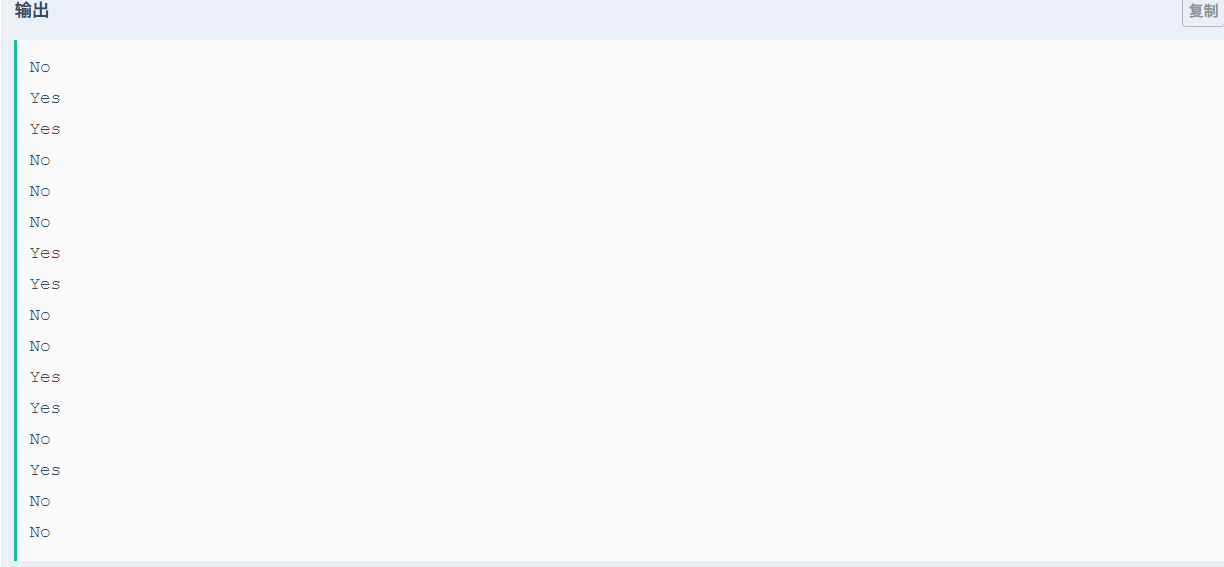
思路：观察到开始的时候在1-n中选p，这个p是有a+b/a-b的性质的。

我们现在先把a+b记为c,a-b记为d；这个c是a*x1+b*y1的一种形式，同理这个d也是a*x2+b*y2的一种形式

那么下一次拿的数字为a+c,a-c,b+c,b-c;将c/d换成上一行提到的形式，可得下一次拿的都是 a*x+b*y的形式，那么我们可以知道p=a*x+b*y,那么p是gcd（a,b)的倍数，于是在1-n中算出有多少个gcd(a,b)的倍数，如果是奇数那么先手赢

反思：如果一个数能表示成p=a*x+b*y，那么p是gcd(a,b）的倍数

简单理解：gcd(a,b)=d;那么p=d*(x+?)+b*(y+?);

#include<iostream>
#include<vector>
#include<queue>
#include<cstring>
#include<algorithm>
using namespace std;
const int maxn=1e5;
typedef long long LL;

LL gcd(LL a,LL b)
{
	return b?gcd(b,a%b):a;
}
int main(void)
{
	LL t;cin>>t;
	while(t--)
	{
		LL n,a,b;cin>>n>>a>>b;
		LL k=n/gcd(a,b);
        k-=2;
		if( k>0 && k%2==1 ) cout<<"Yes"<<endl;
		else cout<<"No"<<endl;
	} 

return 0;
}