一、题目描述

以二叉链表作为二叉树的存储结构，编写下列算法：

1）判别两棵树是否相等

2）交换二叉树每个结点的左孩子和右孩子

3）计算二叉树的最大宽度（二叉树的宽度是指二叉树所有层中结点个数的最大值）

二、解答

1）判别两棵树是否相等

算法思想：

利用递归实现，递归结束的条件有三个：一是两棵树均为空，返回相等；二是只有一棵树为空，返回不等；三是根结点的数据域不等，返回不等。其他情况下则递归判断相应的孩子结点是否相等。

算法描述：

int Compare(BiTree T1,BiTree T2)
{
    if(T1==NULL&&T2==NULL)
    {
        return 1;
    }
    else if(T1==NULL||T2==NULL)
    {
        return 0;
    }
    if(T1->data!=T2->data)
    {
        return 0;
    }
    int left=right=0;
    left=Compare(T1->lchild,T2->lchild);
    right=Compare(T1->rchild,T2->rchild);
    return left&&right;
    
}

具体代码：

#include<stdio.h>
#include<stdlib.h>
/*二叉树结点*/
typedef struct BiTNode
{
	char data;
	struct BiTNode* lchild, * rchild;
}BiTNode,*BiTree;

/*先序遍历，创建二叉树*/
void CreatBiTree(BiTree& T)
{
	char ch;
	scanf("%c", &ch);
	getchar();
	if (ch == '#')
	{
		T = NULL;
	}
	else
	{
		T = (BiTNode*)malloc(sizeof(BiTNode));
		T->data = ch;
		printf("请输入%c的左子树：\n", ch);
		CreatBiTree(T->lchild);
		printf("请输入%c的右子树：\n", ch);
		CreatBiTree(T->rchild);
	}
}
/*先序打印二叉树*/
void InOrderPrint(BiTree T)
{
	if (T == NULL)
	{
		return;
	}
	else
	{
		printf("%c ", T->data);
		InOrderPrint(T->lchild);
		InOrderPrint(T->rchild);
	}
}
/*Compare函数，比较两二叉树是否相等*/
int Compare(BiTree T1, BiTree T2)
{
	if (T1 == NULL && T2 == NULL)//两树均为空
	{
		return 1;
	}
	else if (T1 == NULL || T2 == NULL)//一树为空，另一树不为空
	{
		return 0;
	}
	if (T1->data != T2->data)//两树对应结点的数据域不同
	{
		return 0;
	}
	int left = 0, right = 0;//比较左右子树
	left = Compare(T1->lchild, T2->lchild);
	right = Compare(T1->rchild, T2->rchild);
	return left && right;


}
int main()
{
	BiTree T1, T2;
	printf("创建第一个二叉树：\n");
	CreatBiTree(T1);
	InOrderPrint(T1);
	printf("\n创建第二个二叉树：\n");
	CreatBiTree(T2);
	InOrderPrint(T2);
	if (Compare(T1, T2))
	{
		printf("\n两二叉树相同\n");
	}
	else
	{
		printf("\n两二叉树不同\n");
	}
	return 0;
}

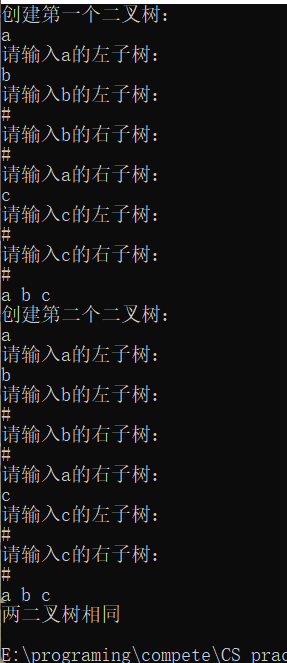
运行结果：

2）交换二叉树每个结点的左孩子和右孩子

算法思想：

如果某结点的左、右子树有一个为空，则返回，否则交换该结点的左右孩子，然后递归交换左右子树。

算法描述：

void ChangeLR(BiTree &T)
{
    BiTree temp;
    if(T->lchild==NULL||T->rchild==NULL)
    {
        return;
    }
    else
    {
        temp=T->lchild;
        T->lchild=T->rchild;
        T->rchild=temp;
    }
    ChangeLR(T->lchild);
    ChangeLR(T-rchild);
}

具体代码：

#include<stdio.h>
#include<stdlib.h>
/*二叉树结点*/
typedef struct BiTNode
{
	char data;
	struct BiTNode* lchild, * rchild;
}BiTNode, * BiTree;

/*先序遍历，创建二叉树*/
void CreatBiTree(BiTree& T)
{
	char ch;
	scanf("%c", &ch);
	getchar();
	if (ch == '#')
	{
		T = NULL;
	}
	else
	{
		T = (BiTNode*)malloc(sizeof(BiTNode));
		T->data = ch;
		printf("请输入%c的左子树：\n", ch);
		CreatBiTree(T->lchild);
		printf("请输入%c的右子树：\n", ch);
		CreatBiTree(T->rchild);
	}
}
/*先序打印二叉树*/
void InOrderPrint(BiTree T)
{
	if (T == NULL)
	{
		return;
	}
	else
	{
		printf("%c ", T->data);
		InOrderPrint(T->lchild);
		InOrderPrint(T->rchild);
	}
}
/*交换二叉树的左右孩子*/
void ChangeLR(BiTree& T)
{
	BiTree temp;
	if (T->lchild == NULL || T->rchild == NULL)
	{
		return;
	}
	else
	{
		temp = T->lchild;
		T->lchild = T->rchild;
		T->rchild = temp;
	}
	ChangeLR(T->lchild);
	ChangeLR(T->rchild);
}
int main()
{
	BiTree T1;
	printf("创建一个二叉树：\n");
	CreatBiTree(T1);
	printf("二叉树为：\n");
	InOrderPrint(T1);
	printf("交换左右孩子之后的二叉树为：\n");
	ChangeLR(T1);
	InOrderPrint(T1);
	return 0;
}

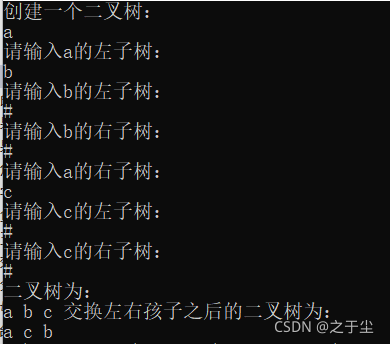
运行结果：

3）计算二叉树的最大宽度

算法思想：

计算二叉树最大的宽度可采用层次遍历的方法，利用队列来实现。首先判断是否为空树，如果为空树，则宽度为0；不为空，则分别记录局部的宽度和当前的最大宽度，逐层遍历结点，如果结点有孩子结点，则将孩子结点加入队尾；每层遍历完毕后，若局部宽度打于当前的最大宽度，则修改最大宽度。

算法描述：

int Width(BiTree T)
{
    if(T==NULL)
    {
        return 0;
    }
    else
    {
        BiTree Q[];//Q是队列，元素为二叉树结点指针，容量足够大
        front=1;//队头指针
        rear=1;//队尾指针
        last=1;//同层最右结点在队列中的位置
        temp=0;//局部宽度
        maxw=0；//最大宽度
        Q[rear]=T;//根结点入队
        while(front<=last)
        {
            p=Q[front++];
            temp++;//同层元素加1
            if(p->lchild!=NULL)
            {
                Q[++rear]=p->lchild;//左孩子入队
            }
            if(p->rchild!=NULL)
            {
                Q[++rear]=p->rchild;//右孩子入队
            }
            if(front>last)//一层结束
            {
                last=rear;//last指向下层最右元素
                if(temp>maxw)
                {
                    maxw=temp;//更新当前最大宽度
                }
                temp=0;
            }
        }
        return maxw;
    }
}

具体代码：

#include<stdio.h>
#include<stdlib.h>
/*二叉树结点*/
typedef struct BiTNode
{
	char data;
	struct BiTNode* lchild, * rchild;
}BiTNode, * BiTree;

/*先序遍历，创建二叉树*/
void CreatBiTree(BiTree& T)
{
	char ch;
	scanf("%c", &ch);
	getchar();
	if (ch == '#')
	{
		T = NULL;
	}
	else
	{
		T = (BiTNode*)malloc(sizeof(BiTNode));
		T->data = ch;
		printf("请输入%c的左子树：\n", ch);
		CreatBiTree(T->lchild);
		printf("请输入%c的右子树：\n", ch);
		CreatBiTree(T->rchild);
	}
}
/*先序打印二叉树*/
void InOrderPrint(BiTree T)
{
	if (T == NULL)
	{
		return;
	}
	else
	{
		printf("%c ", T->data);
		InOrderPrint(T->lchild);
		InOrderPrint(T->rchild);
	}
}
int Width(BiTree T)
{
    if (T == NULL)
    {
        return 0;
    }
    else
    {
        BiTree Q[100], p;//Q是队列，元素为二叉树结点指针，容量足够大
        int front = 1;//队头指针
        int rear = 1;//队尾指针
        int last = 1;//同层最右结点在队列中的位置
        int temp = 0;//局部宽度
        int maxw = 0;//最大宽度
        Q[rear] = T;//根结点入队
        while (front <= last)
        {
            p = Q[front++];
            temp++;//同层元素加1
            if (p->lchild != NULL)
            {
                Q[++rear] = p->lchild;//左孩子入队
            }
            if (p->rchild != NULL)
            {
                Q[++rear] = p->rchild;//右孩子入队
            }
            if (front > last)//一层结束
            {
                last = rear;//last指向下层最右元素
                if (temp > maxw)
                {
                    maxw = temp;//更新当前最大宽度
                }
                temp = 0;
            }
        }
        return maxw;
    }
}
int main()
{
	BiTree T1;
	printf("创建一个二叉树：\n");
	CreatBiTree(T1);
	printf("二叉树为：\n");
	InOrderPrint(T1);
    int x = Width(T1);
    printf("二叉树的最大宽度为：%d", x);
	return 0;
}

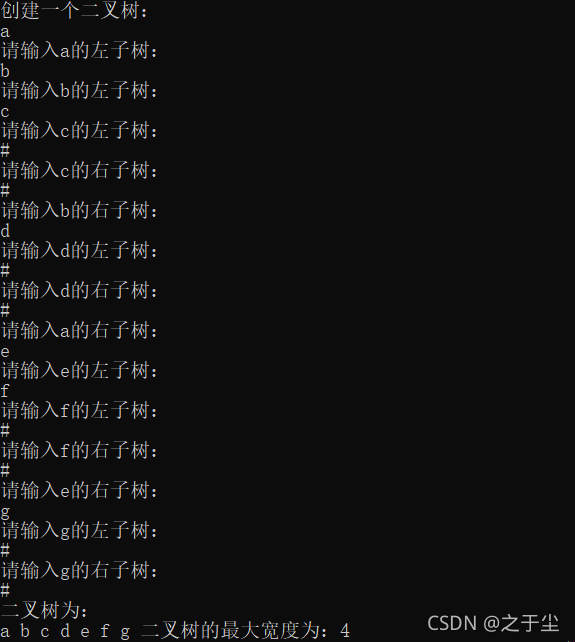
运行结果：