简介
得到矩阵 Q, K, V之后就可以计算出 Self-Attention 的输出了,计算的公式如下:
A
t
t
e
n
t
i
o
n
(
Q
,
K
,
V
)
=
S
o
f
t
m
a
x
(
Q
K
T
d
k
)
V
Attention(Q,K,V)=Softmax(\frac{QK^T}{\sqrt{d_k}})V
Attention(Q,K,V)=Softmax(dkQKT)V
好处
除以维度的开方,可以将数据向0方向集中,使得经过softmax后的梯度更大.
从数学上分析,可以使得QK的分布和Q/K保持一致,
推导
对于两个独立的正态分布而言,两者的加法的期望和方差就是两个独立分布的期望和方差。
qk_T的计算过程为[len_q,dim][dim,len_k]=[len_q,len_k],qk的元素等于dim个乘积的和。对于0-1分布表乘积不会影响期望和方差,但是求和操作会使得方差乘以dim,因此对qk元素除以sqrt(dim)把标准差压回1.
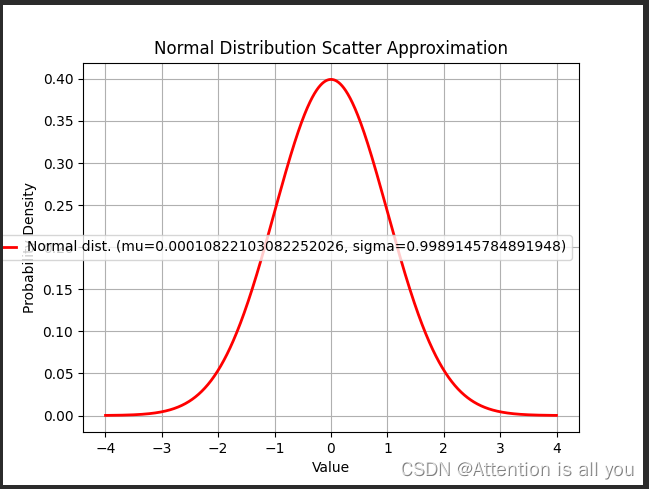
这里展示一个不严谨的采样可视化过程
假设在query在(0,1)分布,key在(0,1)分布,随机采样lengthdim个点,然后统计querykey_T的散点的分布
import math
import numpy as np
import matplotlib.pyplot as plt
def plot_curve(mu=0, sigma =1):
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
# 设置正态分布的参数
# mu, sigma = 0, 1 # 均值和标准差
# 创建一个x值的范围,覆盖正态分布的整个区间
x = np.linspace(mu - 4 * sigma, mu + 4 * sigma, 1000)
# 计算对应的正态分布的概率密度值
y = norm.pdf(x, mu, sigma)
# 我们可以选择y值较高的点来绘制散点图,以模拟概率密度的分布
# 这里我们可以设置一个阈值,只绘制y值大于某个值的点
threshold = 0.01 # 可以根据需要调整这个阈值
selected_points = y > threshold
plt.plot(x, y, 'r-', lw=2, label='Normal dist. (mu={}, sigma={})'.format(mu, sigma))
plt.title('Normal Distribution Scatter Approximation')
plt.xlabel('Value')
plt.ylabel('Probability Density')
plt.legend()
plt.grid(True)
plt.show()
def plot_poins(x):
# 因为这是一个一维的正态分布,我们通常只绘制x轴上的点
# 但为了模拟二维散点图,我们可以简单地将y轴设置为与x轴相同或固定值(例如0)
y = np.zeros_like(x)
# 绘制散点图
plt.figure(figsize=(8, 6))
plt.scatter(x, y, alpha=0.5) # alpha控制点的透明度
plt.title('Normal (0, 1) Distribution Scatter Plot')
plt.xlabel('Value')
plt.ylabel('Value (or Frequency if binned)')
plt.grid(True)
plt.show()
if __name__ == '__main__':
# 设置随机种子以便结果可复现
np.random.seed(0)
len = 10000
dim = 100
query = np.random.normal(0, 1, len*dim).reshape(len,dim)
key = np.random.normal(0, 1, len*dim).reshape(dim,len)
qk = np.matmul(query,key) / math.sqrt(dim)
mean_query = query.mean()
std_query = np.std(query,ddof=1)
mean_key = key.mean()
std_key = np.std(key,ddof=1)
mean_qk = qk.mean()
std_qk = np.std(qk,ddof=1)
plot_poins(query)
plot_curve(mean_query,std_query)