Bootstrap

堆排序及其时间复杂度（C语言）

如何将一个随机数组按照升序或降序的方式排序？方法应该多种多样，今天我们就来介绍一下堆排序这种方式。
这部分内容需要多消化，因为各个函数与概念之间错综复杂，大家需要捋清楚各个函数与操作之间的调用关系。

堆排序

堆的基本操作中的时间复杂度（基础）

在堆的基本操作中，消耗时间最多的函数就是HeapPush（在堆中插入新元素）和HeapPop（删除堆顶），更确切地说，是各自包含的AdjustUp（向上调整）和AdjustDown（向下调整）函数。因此，考虑堆操作的时间复杂度就要从这两部分入手。
我们先来复习一下这两组操作，这里我们先以插入操作以及向上调整为例：

void HeapPush(Heap* hp,HpDataType x)
{
    assert(hp);
    if(hp->size==hp->capacity)
    {
        int newcapacity=hp->capacity==0?4:2*hp->capacity;
        HpDataType* tmp=realloc(hp->a,newcapacity*sizeof(HpDataType));
        if(tmp==NULL)
        {
            printf("error");
            exit(1);
        }
        hp->a=tmp;
        hp->capacity=newcapacity;
    }
    hp->a[hp->size]=x;
    AdjustUp(hp->a,hp->size);
    hp->size++;
}

void AdjustUp(HpDataType*a,int child)
{
    int parent=(child-1)/2;
    while(child>0)
    {
        if(a[child]<a[parent])//如果是大堆，那么这里改成大于号即可
        {
            Swap(&a[child],&a[parent]);
            child=parent;
            parent=(parent-1)/2;
        }
        else
            break;
    }
}
HpDataType Swap(HpDataType* pa,HpDataType* pb)
{
    HpDataType tmp = *pa;
    *pa=*pb;
    *pb=tmp;   
}

具体操作的详细讲解见我的另一篇文章：
（C语言）堆的实现:https://blog.csdn.net/zxy13149285776/article/details/137885563?spm=1001.2014.3001.5501
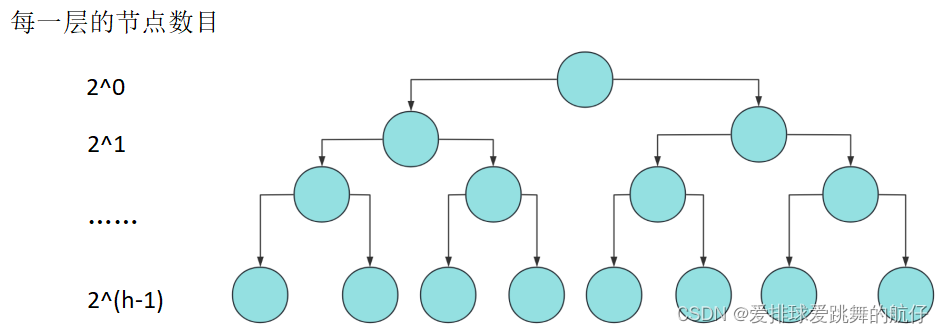
接下来，我们先来讨论满二叉树的节点数目N与高度h之间的关系：

在这里插入图片描述

N=2^0 + 2^1 + 2^2 + … + 2^(h-1) 这样，我们就得到了满二叉树节点总数与高度关系:
N=2^n-1;
h=log (N+1) 注意，我们这里省略了底数2

我们再来以完全二叉树中的极端情况讨论：

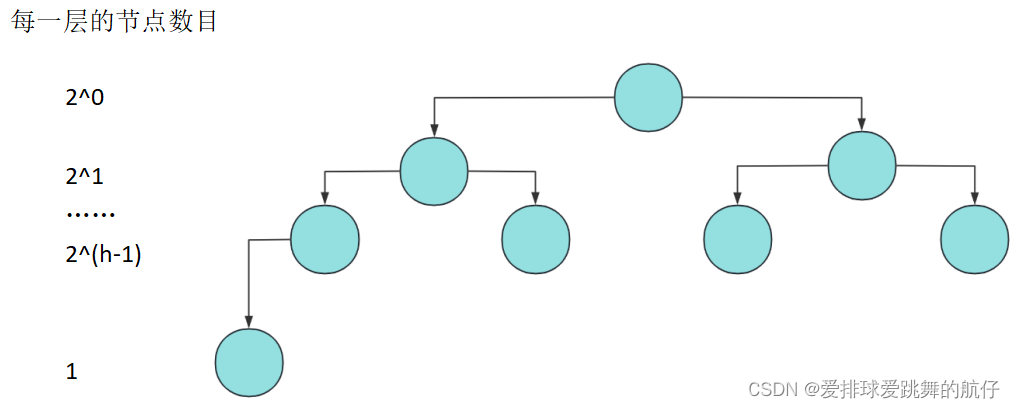
在这里插入图片描述易得到：
N = 2 ^ (h - 1)
h = log (N + 1)

  • 在HeapPushz中，每插入一个就要进行向上调整操作，那么该插入的元素，最多向上调整h次。
    例如，在小堆最后插入一个超级大数，那么AdjustUp中的while语句执行一次，然后break;
    如果是插入一个比所有数都小的数，那么while执行高度h次，然后再跳出循环。那么最多执行h次，
    对于满二叉树，h=log (N+1），对于完全二叉树，h=log N +1，那么两种情况下，一次向上调整的时间复杂度都为O(log N);
  • 同理，在HeapPop操作中，while语句也是最多执行h次，也就是说，每个元素最多向下调整h次，那么时间复杂度同样也是O（log N）；
  • 注意，我们这里所讲的向上和向下调整的时间复杂度，都是指的一次调整，也就是只调整一个元素，不要跟后续内容的时间复杂度搞混哟~
  • 那么堆基本操作的时间复杂度就到这里，后面的内容都要用到我们这里所推导出的基础。

数组建堆

  • 在上一篇文章（见前文链接）的最后，我们提到了一种数组建堆的方式：
int a[6]={50,100,70,65,60,32};
Heap hp;
HeapInit(&hp);
for(int i=0;i<sizeof(a)/sizeof(a[0]);i++)
{
    HeapPush(&hp,a[i]);
}

这种方法是可行的，但是这种方式时间复杂度较高。这段代码实际上是内外两层循环，第一层循环进行sizeof(a)/sizeof(a[0])次，也就是N次，而内层循环HeapPush我们在上一段中已经算出了时间复杂度：O（logN）,那么，总的建堆时间复杂度就为O（N*log N）。
下述方式效率更高：

void HpInitArray(Hp* php,HpDataType* a,int n)
//这里的a是我们要建堆的数组，n是数组元素个数
{
    assert(php);
    php->a=(HpDataType*)malloc(sizeof(HpDataType)*n);
    //从这儿可以看出，不用初始化变量堆
    if(php->a==NULL)
    {
        printf("fail malloc");
        exit(1);
    }
    memcpy(php,a,sizeof(HpDataType)*n);//memcpy的头文件是<string.h>
    php->size=php->capacity=n;
    //接下来就开始建堆了，我们这里先把建堆部分空出来，因为后续要比较向上和向下两种方式，因此这里先空着
    /*


    未完待续……

   */
}
int main()
{
    int a[6]={50,100,70,65,60,32};
    Heap hp;
    HpInitArray(&hp,a,sizeof(a)/sizeof(a[0]);
}

为什么效率更高呢？我们先看下面两种建堆方式，通过比较时间复杂度，就知道了。

两种调整方式（向上调整和向下调整）的比较

在上一段代码中，我们只进行到把待处理的数组放进堆结构中的数组中这一步，但数组中元素还没有满足堆的要求，即元素不满足大堆或小堆结构。那么我们现在来对元素进行调整。
有两种方式，一种是向上调整，一种是向下调整，我们接下来通过分析两者的时间复杂度来进行比较：

向上调整

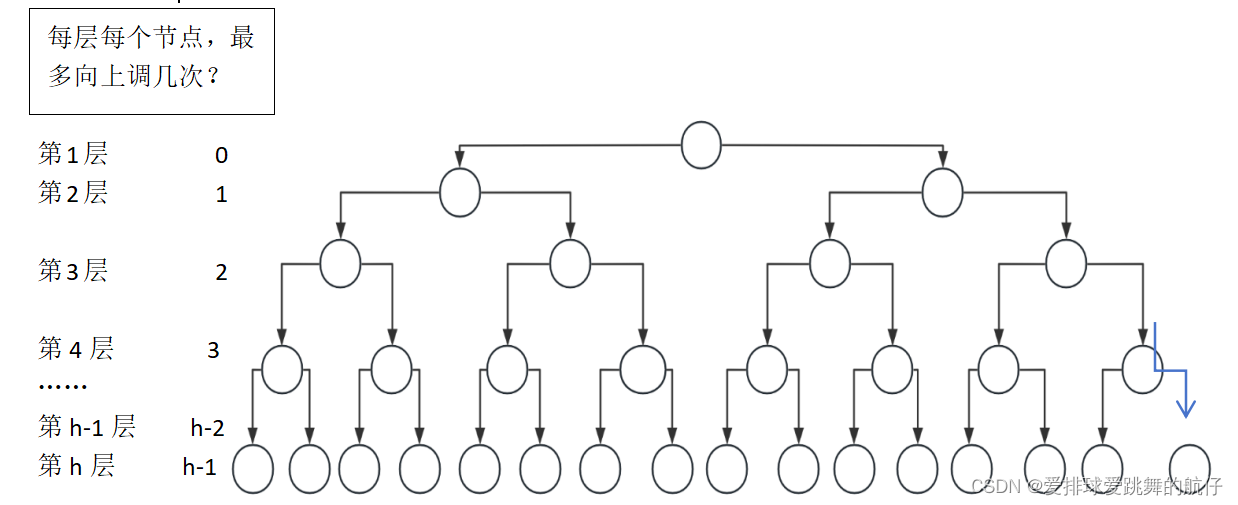
在这里插入图片描述累计向上调整的次数F(h)=每一层的节点个数*它最多向上调整的次数

=2 ^ 1 * 2 + 2 ^ 2 * 2 + 2 ^ 3 * 3 + …… + 2 ^ ( h - 2 ) * ( h - 2) + 2 ^ ( h - 1) * ( h - 1 )

= 2 ^ h *( h - 2 ) + 2

再用我们刚刚第一部分推导出的h与N的关系：h=log (N + 1），我们这里就先以满二叉树为例，完全二叉树和满二叉树虽有不同，但算出来都是一个数量级。
则F（N）= （ N + 1 ）* [log (N + 1) - 2] + 2
这样，我们很容易就得到，向上调整建堆的时间复杂度为O（N * log N）；

我们来看具体代码：

for(int i=1;i<php->size;i++)
{
    AdjustUp(php->a,i);
}

几点说明：

  • 首先，i的初始值为1，是因为，第一个元素没有父节点，不用向上调
  • 其次，AdjustU的第一个参数是要调整的数组，第二个参数则是当前要向前调整的元素的下标，形参名为child。

向下调整

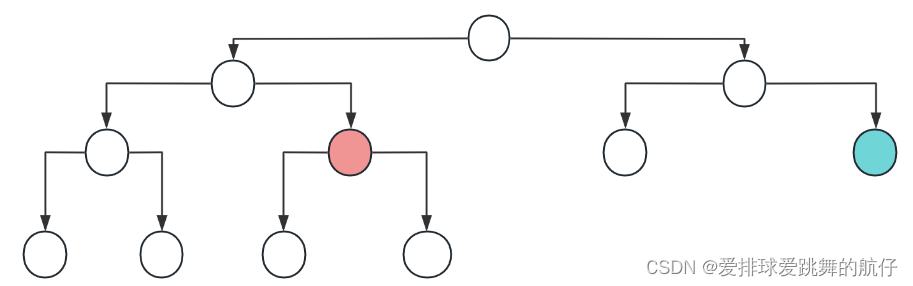
向下调整，我们是从倒数第一个非叶节点开始向下调整的 ，相当于先把每一个子树调成堆，再累计把大树调成堆。为什么叶节点不用调?因为叶节点没有子节点，没法下调。

  • 注意，这里的倒数第一个非叶节点 ≠ 倒数第二行最后一个节点，对于满二叉树来说，是相等的，对于完全二叉树来说，不一样，如图：
    在这里插入图片描述
  • 该图中，倒数第一个非叶节点应该是红色节点，而非蓝色节点

下一个问题就是，怎么找倒数第一个非叶节点呢？
这就要用到我们上一篇文章中讲到的父节点与子节点下标关系：

  • parent = （child - 1）/2

而最后一个叶节点的下标为php->size - 1，因此，最后一个非叶节点，即最后一个叶节点的父节点（理解不了的同学画画图哦~）的下标就是（php - >size - 1 - 1）/ 2;调整到第一个元素为止

for(int i=(php - >size - 1 - 1)/ 2;i>=0;i++)
{
    AdjustDown(php->a,php->size,i);//要建成大堆还是小堆由AdjustDown里面的判断决定
}

这里第二个参数为数组元素个数，用于判断向下调整过程中是否已经遍历到了叶节点。
第三个参数为当前调整元素的下标，用于在函数内部找到该元素对应的两个子节点。
接下来我们来计算向下调整的时间复杂度：
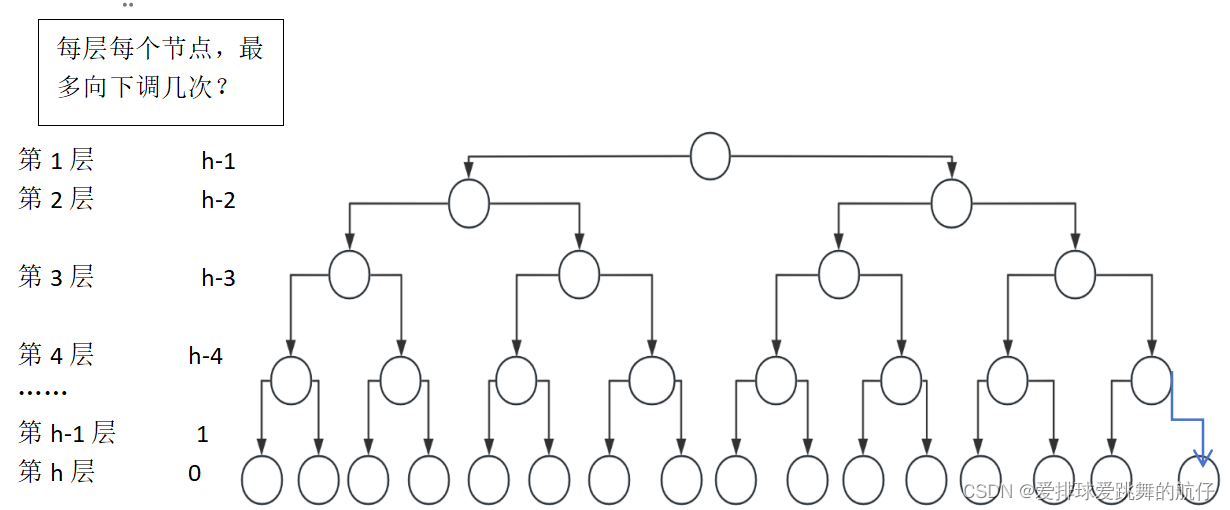
在这里插入图片描述累计调整次数F（h）= 2 ^ ( h - 2 ) * 1 + 2 ^ ( h - 3 ) * 2 + …… + 2 ^ 1 * ( h - 2 ) + 2 ^ 0 * ( h - 1 )

  • 这里，我们用高中学的错位相减法就可以解得：
  • F（h）= 2 ^ h - 1 - h
  • F （N）= N - log (N + 1 )
    所以，向下调整的时间复杂度为O（N）。

因此，向下调整的时间复杂度要小于向上调整。那么为什么会出现这种情况呢？
我们观察两个F(h)的原始计算公式，会发现：
向上调整：某一层如果节点个数多，那么调整次数也多，即每一项都是多 * 多；
向下调整：越往下，节点数量越多，但调整次数越少，例如最后一层，数量多，但一次都不用调，因此每一项都为多 * 少

因此，一般建堆时，我们都是用向下调整的方式进行，效率高。回到我们刚刚没写完的HpInitArray函数：
“未完待续”部分即为向下调整部分代码：

for(int i=(php - >size - 1 - 1)/ 2;i>=0;i--)
{
    AdjustDown(php->a,php->size,i);//要建成大堆还是小堆由AdjustDown里面的判断决定
}

主函数：

int main()
{
    int a[6]={50,100,70,65,60,32};
    Heap hp;
    HpInitArray(&hp,a,sizeof(a)/sizeof(a[0]);
}

时间复杂度仅为O（N），小于之前的O（N * log N）。

堆排序

至此，我们已将数组建成了堆。那么，如果我们想更进一步地调整数组，使其成为一个升序或降序的数组，该怎么办呢?
我们接下来来介绍堆排序：
首先有一种好想的方法：

void HeapSort(int *a,int n)
{
    HP hp;
    HpInitArray(&hp,a,n);
    
    int i=0;
    while(!HpEmpty(&hp))
    {
        a[i++]=HpTop(&hp);
        HpPop(&hp);
    }
    HpDestroy(&hp);
}
int main()
{
    int a[]={9,8,3,7,6,1,2,5,4,0};
    HeapSort(&a,sizeof(a)/sizeof(int));
}

这个方法的大致思路就是，先建堆，然后依次取堆顶，进行排序。
但接下来要介绍的这种方法就有点东西了，甚至，
不用定义堆！！！
啊？不用建堆那还怎么堆排序啊？是这样的，堆排序，未必要做一个堆出来，堆的结构本质是数组，那么我们针对数组来巧妙操作就可以完成，省去大量时间来写定义堆相关的函数。

我们先来看这种方法的第一部分代码：

void HeapSort(int *a,int n)
{
    for(int i=(n-1-1)/2;i>=0;i--)
    {
        AdjustDown(a,n,i);
    }
    /*

    未完待续……

    */
}

这种方式和上一种方式的区别就是，这种方式的向调整直接在sort函数内进行，而上一种则是打包在HpInitArray函数里进行。实际上，大家仔细想一想，先把数组放在一个堆结构里，然后再进行向下调整，是不是有点画蛇添足呢？我为什么不能直接把数组进行向下调整，而要多出一步，先把它放进一个堆呢？数组本身根本没有变化啊。

其次，这种写法也解释了为什么AdjustDown的第一个参数不写堆指针，而是数组了，因为堆的插入和删除需要用到向上向下调整函数，但是用向上向下调整函数的时候，我们未必需要堆。因此用数组，可以拓宽用法。

建大堆还是建小堆的问题

那么，接下来，我们要解决的就是，如果要将堆排成升序数组或降序数组，那么应该建大堆还是建小堆呢？
我们以将下述数组转为升序数组为例：

int a[]={9,8,3,7,6,1,2,5,4,0};

很多人第一反映应该都是建小堆，然后依次取堆顶。
实际不然。
我们来分析一下给这个数组建小堆排序的过程：

  • 通过sort函数内部for循环建堆之后，该数组变为小堆：
  • 在这里插入图片描述
  • 那么此时的堆顶就是最小元素，在数组中应该放在a[0]的位置，并且后续不能再变化。
  • 在这里插入图片描述
  • 如果以a[1]为新的堆顶，那么a[1]到a[n-1]构成的新的堆就为：
  • 在这里插入图片描述
  • 我们发现，这个二叉树的各个元素之间根本没有堆的大小关系，所以，根本不能仅仅用一次向下调整函数来选出次小值，那就只能重新建堆了。
  • 我们上一部分已经知道，建堆的时间复杂度为O(N)，我们要对N个数进行排序，那么就要建堆N次，时间复杂度为O（N^2） , 那还不如遍历一遍排序，复杂度也是O（N^2），我们堆排序的优势就不能体现了。
  • 排升序，建大堆才是正确的。

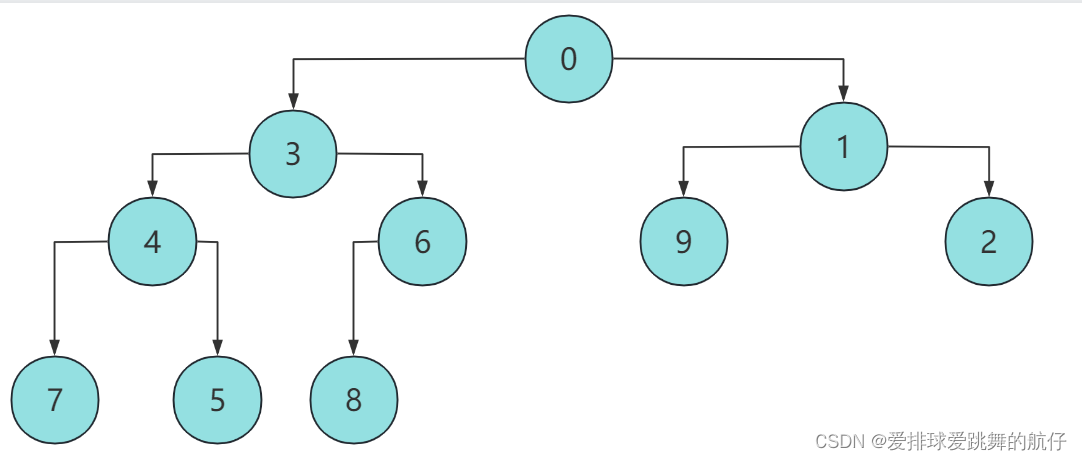
我们接下来分析建大堆，排升序的具体过程：

  • 还是int a[]={9,8,3,7,6,1,2,5,4,0};这个数组，通过sort函数中的for循环建大堆后，变为：
    在这里插入图片描述在这里插入图片描述此时的堆顶9就是最大元素，那么排升序数组，最大的元素应该放在哪儿呢？对，放在数组最后一位，那我们这里将堆顶和堆数组最后一个元素交换：
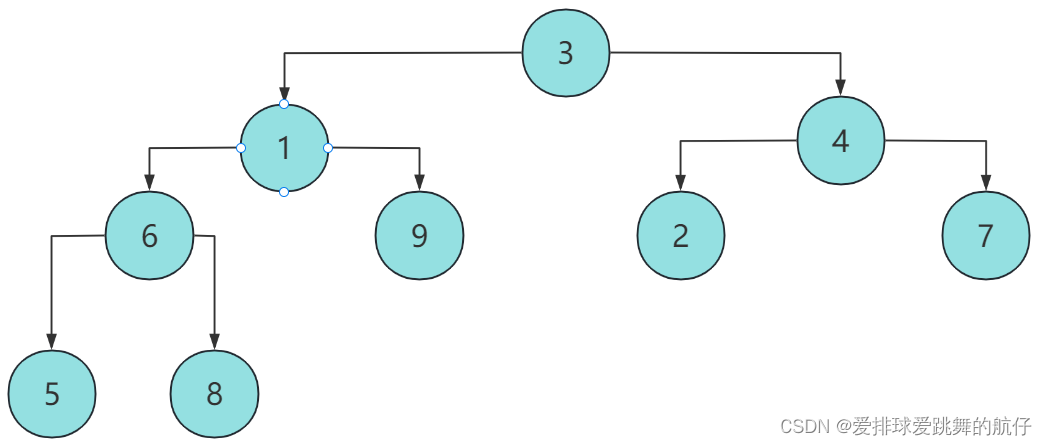
    在这里插入图片描述在数组中体现为：
    在这里插入图片描述
    此时，9就不要再动了。我们看前面9个元素，除了堆顶，其他元素之间都满足大堆条件，那么这个时候我们用一次向下调整，就能重新调整为大堆。调整后的逻辑结构和数组如下：
    在这里插入图片描述在这里插入图片描述这个时候的堆顶元素就是次大元素，我们继续将它和没有排好序的最后一个元素交换，即和4交换，放置在数组倒数第二个位置上，然后让剩余8个元素继续上述操作。

我们接下来看具体代码：

void HeapSort(int *a,int n)
{
    for(int i=(n-1-1)/2;i>=0;i--)
    {
        AdjustDown(a,n,i);
    }
     int end=n-1;
     while(end>0)
     {
         Swap(&a[0],&a[end]);//交换堆顶和最后一个元素
         AdjustDown(a,end,0);
         /*第二个元素表示元素个数，例如，第一步将9和1交换，向下调整的时候
           就不带9调整了，此时向下调整只包括前9个元素，即元素个数为9，即堆尾元素下标
         */
         end--;
     }
}

这种方式的时间复杂度为：O（N * log N）,比刚刚的O（N ^ 2）效率更高。

测试

我们来试试完整代码：

#include<stdio.h>
#include<stdlib.h>
void Swap(int *a,int *b)
{
    int tmp=*b;
    *b=*a;
    *a=tmp;
}
void AdjustDown(int* a,int n,int parent)
{
    int child=parent*2+1;
    while(child<n)
    {
        if(child+1<n&&a[child+1]>a[child])
            ++child;
        if(a[child]>a[parent])
        {
            Swap(&a[child],&a[parent]);
            parent=child;
            child=parent*2+1;
        }
        else
            break;
    }
}
void HeapSort(int *a,int n)
{
    for(int i=(n-1-1)/2;i>=0;i--)
    {
        AdjustDown(a,n,i);
    }

    int end=n-1;
    while(end>0)
    {
        Swap(&a[0],&a[end]);
        AdjustDown(a,end,0);
        end--;
    }
}
int main()
{
    int a[]={0,3,1,4,6,9,2,7,5,8};
    HeapSort(a,sizeof(a)/sizeof(int));

    for(int i=0;i<sizeof(a)/sizeof(int);i++)
    {
        printf("%d ",a[i]);
    }
}

在这里插入图片描述输出的数组已经变为升序数组啦！

今天的分享就到这里，一定要多敲几遍多做题加深印象哦~

悦读

道可道，非常道；名可名，非常名。 无名，天地之始，有名，万物之母。 故常无欲，以观其妙，常有欲，以观其徼。 此两者，同出而异名，同谓之玄，玄之又玄，众妙之门。

最新收录
echarts的温度计 横竖温度计
weblogic卸载
大数据学习之sparkstreaming
java初级开发面试题
多重循环控制
Vue+Element 循环输入框的校验
WAF绕过-漏洞利用篇-sql注入+文件上传-过狗
线性代数的本质（第一部分）
java每日10题
【计算机网络】时延带宽积的理解（图解易懂）
;