1. 判断平衡二叉树
题目解析:
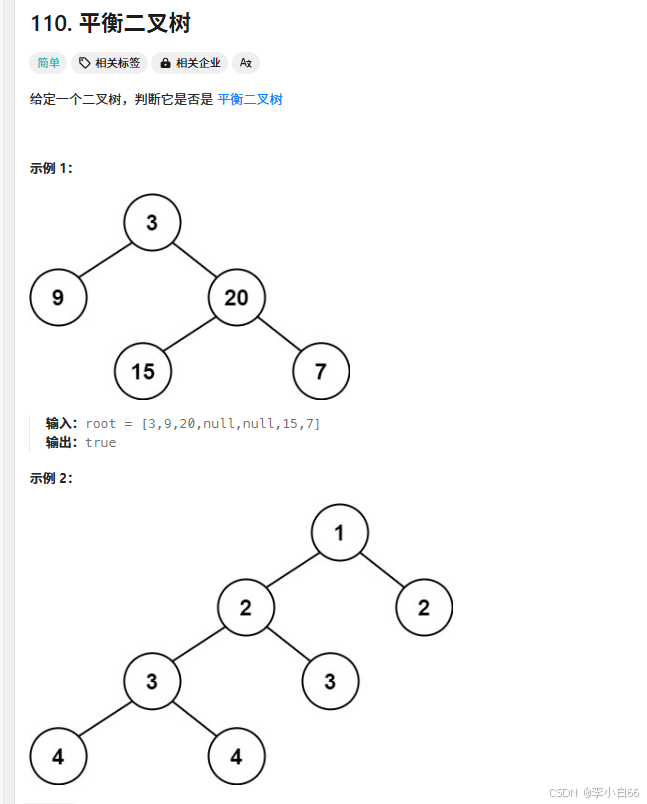
题目:
首先我们要知道什么是平衡二叉树一棵树是否平衡的条件:
当前根结点的左树高度 - 右树高度 <= 1
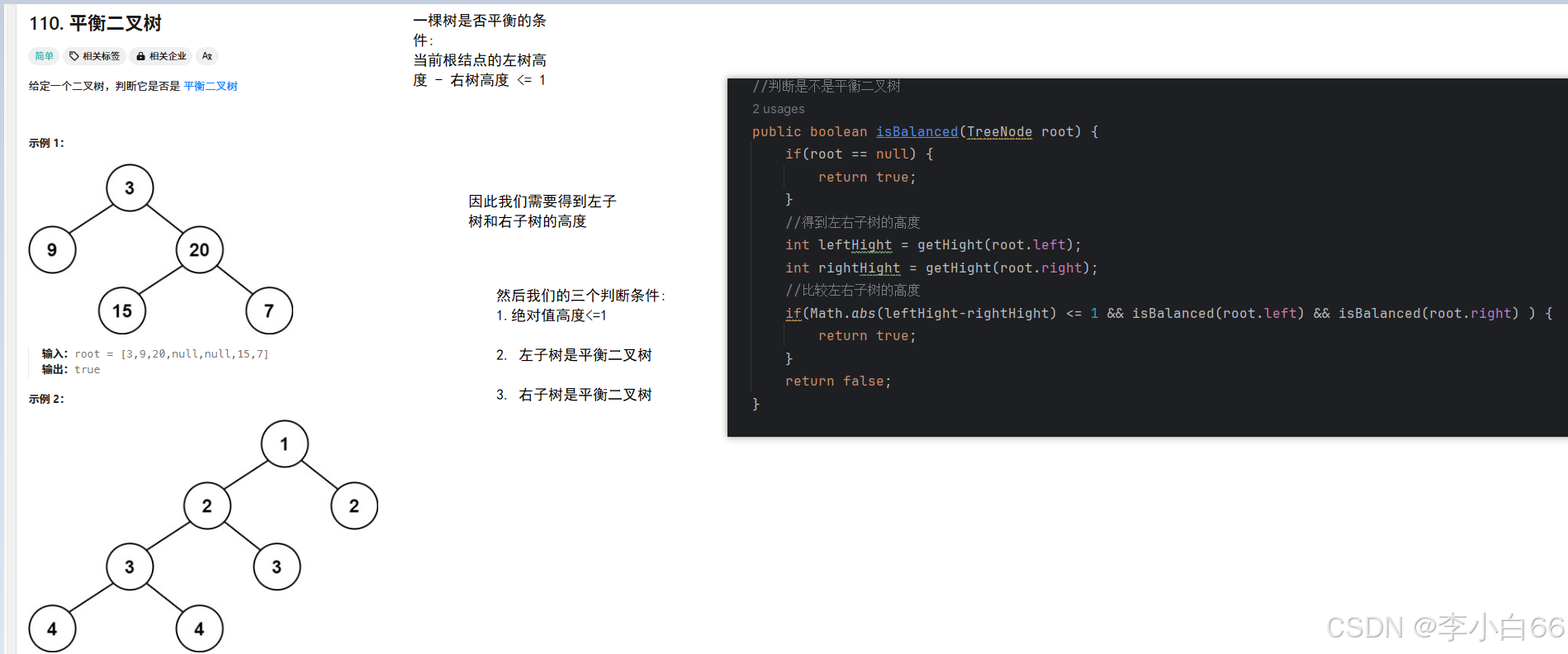
然后我们正式来解题,首先,我们需要判断根结点是不是空的,然后我们需要得到左右子树的高度,最后我们要判断高度绝对值是否<=1,并且我们递归左右子树.
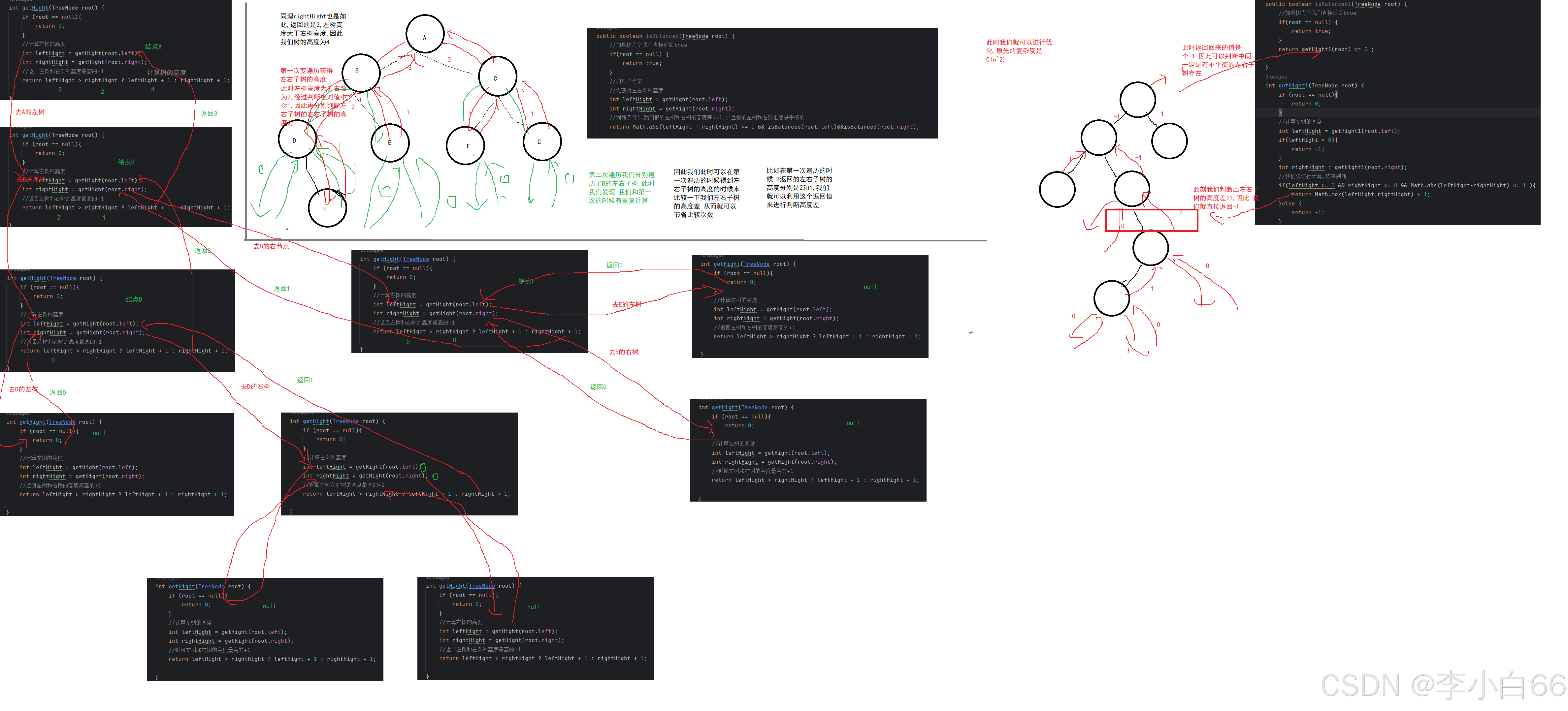
上述的方法时间复杂度是O(n^2),我们可以优化一下,此时我们一边进行计算高度,一边在返回高度的时候我们判断左右高度的绝对值,此时就只是O(n)的时间复杂度.
具体代码:
int getHight(TreeNode root) {
if (root == null){
return 0;
}
//计算左树的高度
int leftHight = getHight(root.left);
int rightHight = getHight(root.right);
//返回左树和右树的高度最高的+1
return leftHight > rightHight ? leftHight + 1 : rightHight + 1;
}
public boolean isBalanced(TreeNode root) {
if(root == null) {
return true;
}
//得到左右子树的高度
int leftHight = getHight(root.left);
int rightHight = getHight(root.right);
//比较左右子树的高度
if(Math.abs(leftHight-rightHight) <= 1 && isBalanced(root.left) && isBalanced(root.right) ) {
return true;
}
return false;
}优化版本的代码:
public boolean isBalanced1(TreeNode root) {
//如果树为空我们直接返回true
if(root == null) {
return true;
}
return getHight1(root) >= 0 ;
}
int getHight1(TreeNode root) {
if (root == null){
return 0;
}
//计算左树的高度
int leftHight = getHight1(root.left);
if(leftHight < 0){
return -1;
}
int rightHight = getHight1(root.right);
//我们边进行计算,边来判断
if(leftHight >= 0 && rightHight >= 0 && Math.abs(leftHight-rightHight) <= 1 ){
return Math.max(leftHight,rightHight) + 1;
}else {
return -1;
}
}2. 判断对称二叉树
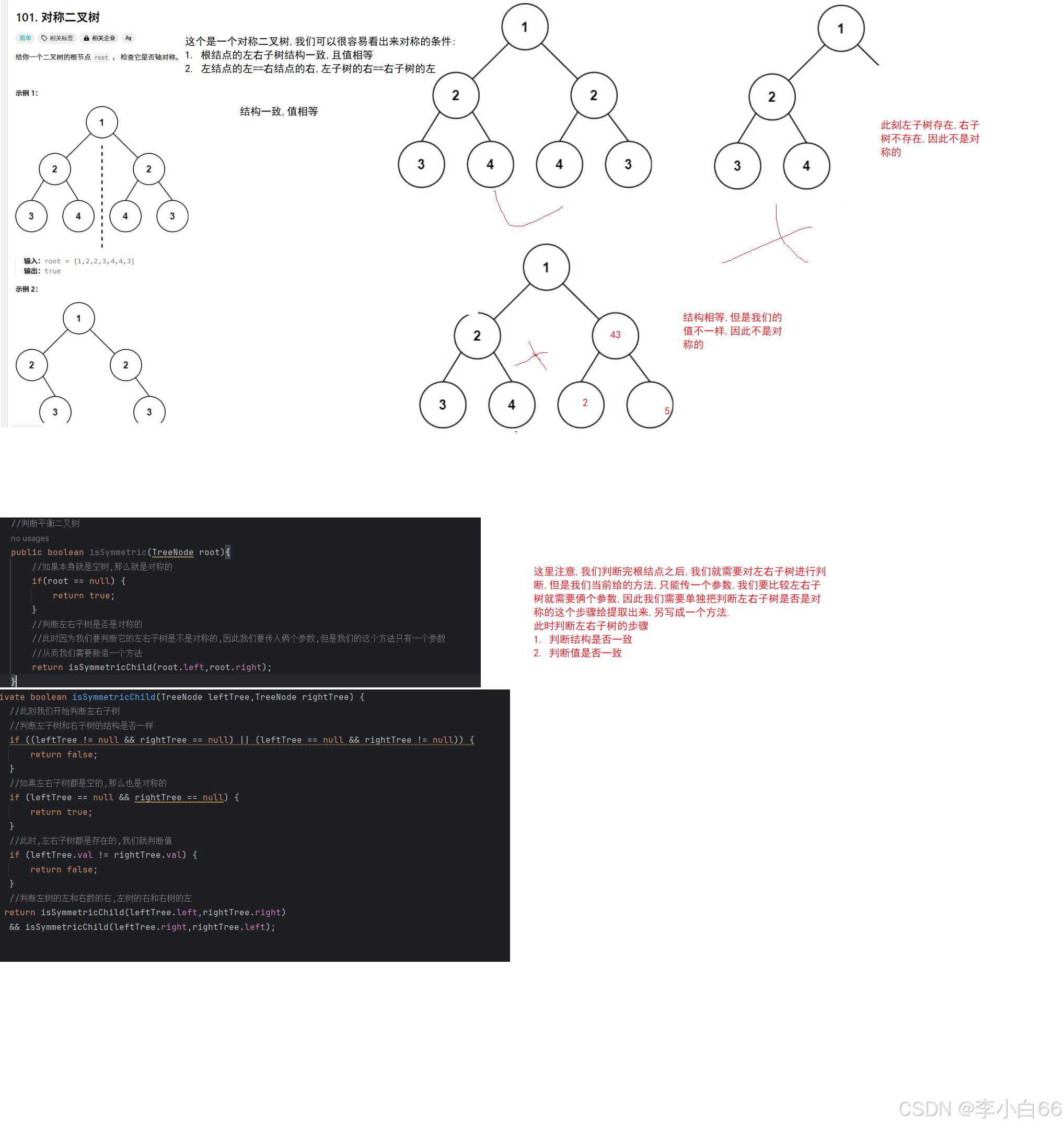
题目解析:
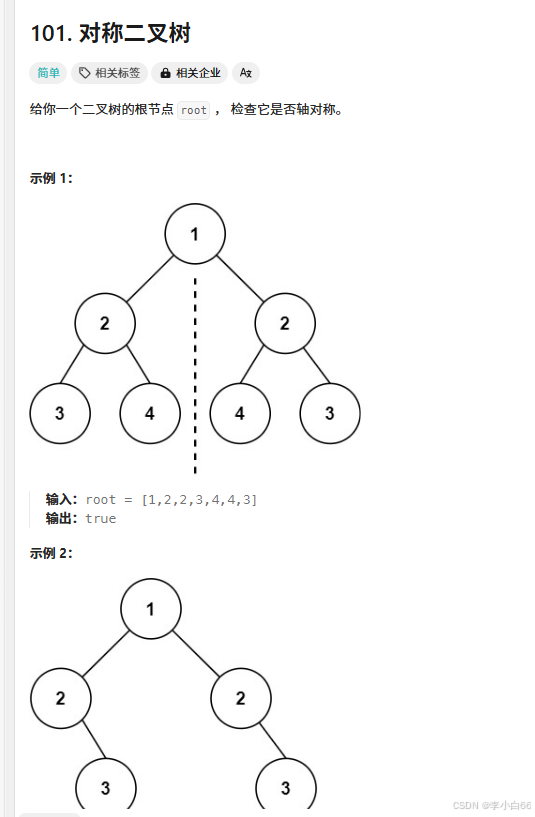
题目:
我们的对称二叉树的判断方式和前面判断俩个树是否完全一样的步骤有些相似.
1> 我们需要判断左右子树的结构是否一致
2> 我们需要判断左右子树的根的值是否一致
3> 我们需要判断左根的左==右根的右,左根的右==右根的左(此刻就需要遍历)
具体代码:
//判断平衡二叉树
public boolean isSymmetric(TreeNode root){
//如果本身就是空树,那么就是对称的
if(root == null) {
return true;
}
//判断左右子树是否是对称的
//此时因为我们要判断它的左右子树是不是对称的,因此我们要传入俩个参数,但是我们的这个方法只有一个参数
//从而我们需要新造一个方法
return isSymmetricChild(root.left,root.right);
}
private boolean isSymmetricChild(TreeNode leftTree,TreeNode rightTree) {
//此刻我们开始判断左右子树
//判断左子树和右子树的结构是否一样
if ((leftTree != null && rightTree == null) || (leftTree == null && rightTree != null)) {
return false;
}
//如果左右子树都是空的,那么也是对称的
if (leftTree == null && rightTree == null) {
return true;
}
//此时,左右子树都是存在的,我们就判断值
if (leftTree.val != rightTree.val) {
return false;
}
//判断左树的左和右数的右,左树的右和右树的左
return isSymmetricChild(leftTree.left,rightTree.right)
&& isSymmetricChild(leftTree.right,rightTree.left);
}3. 二叉树的层次遍历
题目解析:
题目:
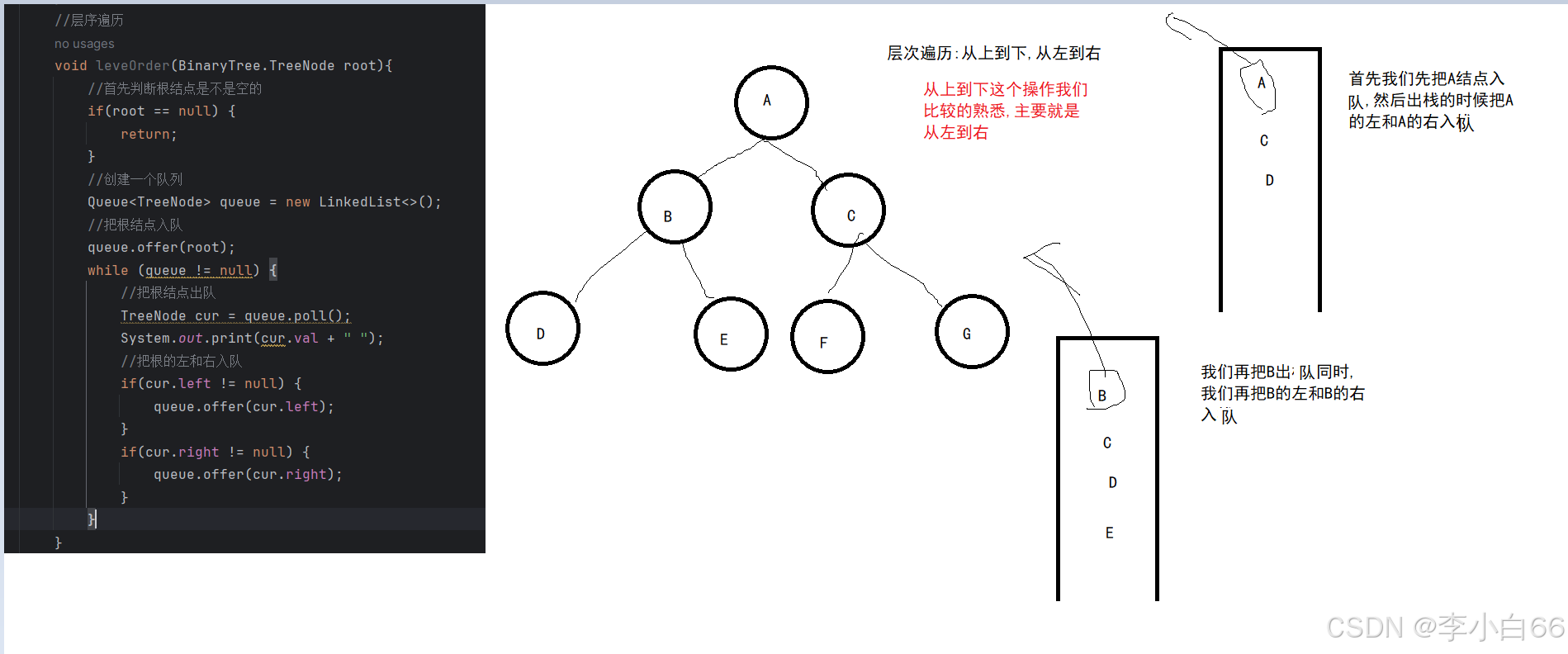
此刻我们先不牵扯到链表,我们先直接先打印出层次遍历,此时我们需要解决的问题是:如何实现从左到右的这个操作,此时我们需要借助一个队列,我们先把根结点入队,然后再出队根结点,再出队(出队的时候打印一下这个元素值)后我们再把根的左和根的右入队,然后再出左的时候把它的左和右入队,就这样一致循环到队空为止.
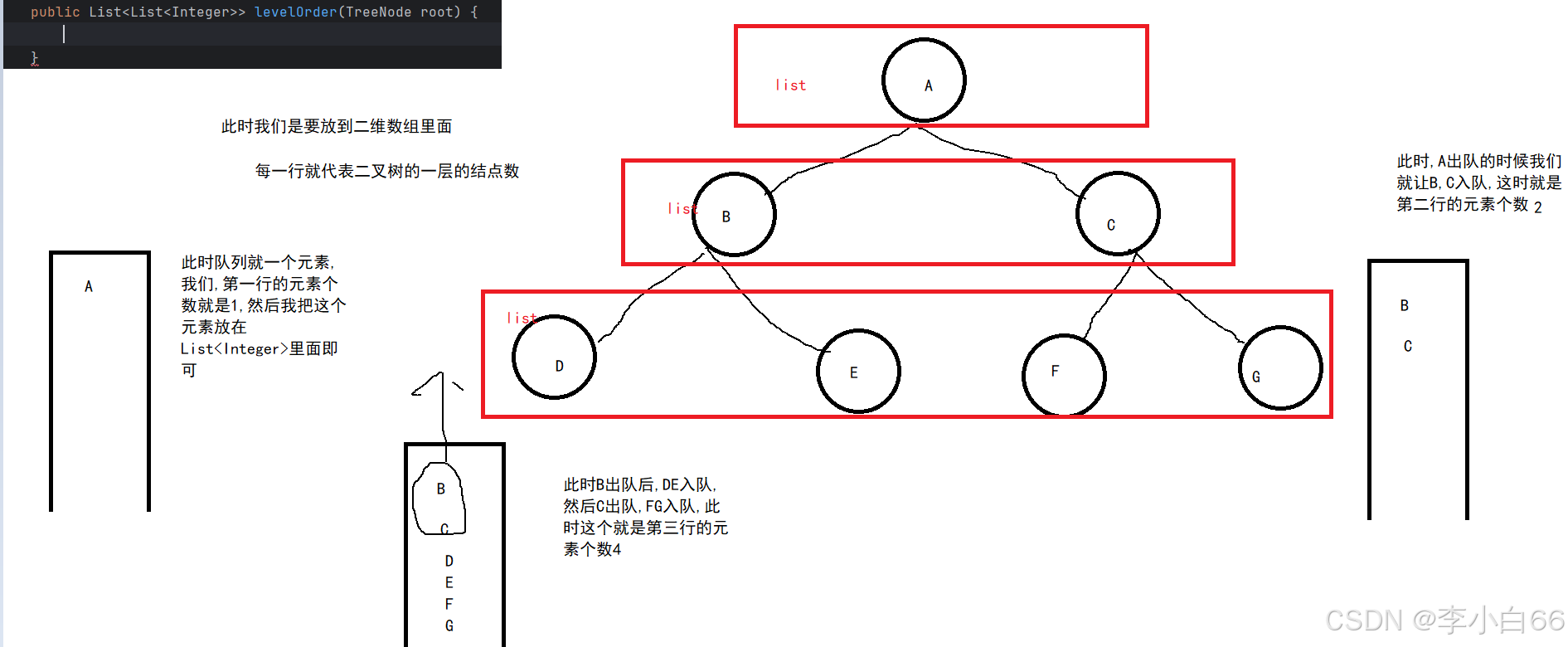
根据题目可知道,我们通过二维数组来保存每一层的结点数目,因此我们需要解决一个问题:我们如何知道每一层的结点数?这个问题还是用队列来解决,当我们的根结点入队的时候,第一层个数为1,根出队的时候,入队A的左和A的右,此时就是第二层的数目,队列大小为2,然后出队B,size--,入队B的左和B的右,再出队Csize--,入队C的左和C的右,此时size的大小为0,我们就知道我们第二行已经创建完成.同样第三行也是如此.最后我们把每一行都加入到二维数组当中即可.
具体代码:
public List<List<Integer>> levelOrder(TreeNode root) {
//首先创建二维数组
List<List<Integer>> list = new ArrayList<>();
//首先判断根结点是不是空的
if(root == null) {
return list;
}
//创建一个队列
Queue<TreeNode> queue = new LinkedList<>();
//把根结点入队
queue.offer(root);
while (!queue.isEmpty()) {
//创建一维数组
List<Integer> tmp = new ArrayList<>();
//计算当前队列大小,也就是当前tmp要加入多少元素
int size = queue.size();
while (size > 0) {
size--;
//把根结点出队
TreeNode cur = queue.poll();
//把根结点加入tmp
tmp.add((int)cur.val);
//把根的左和右入队
if(cur.left != null) {
queue.offer(cur.left);
}
if(cur.right != null) {
queue.offer(cur.right);
}
}
//此时每一行的tmp都构造好了,我们只需要把它放进二维数组即可
list.add(tmp);
}
return list;
}4. 判断完全二叉树
题目解析:
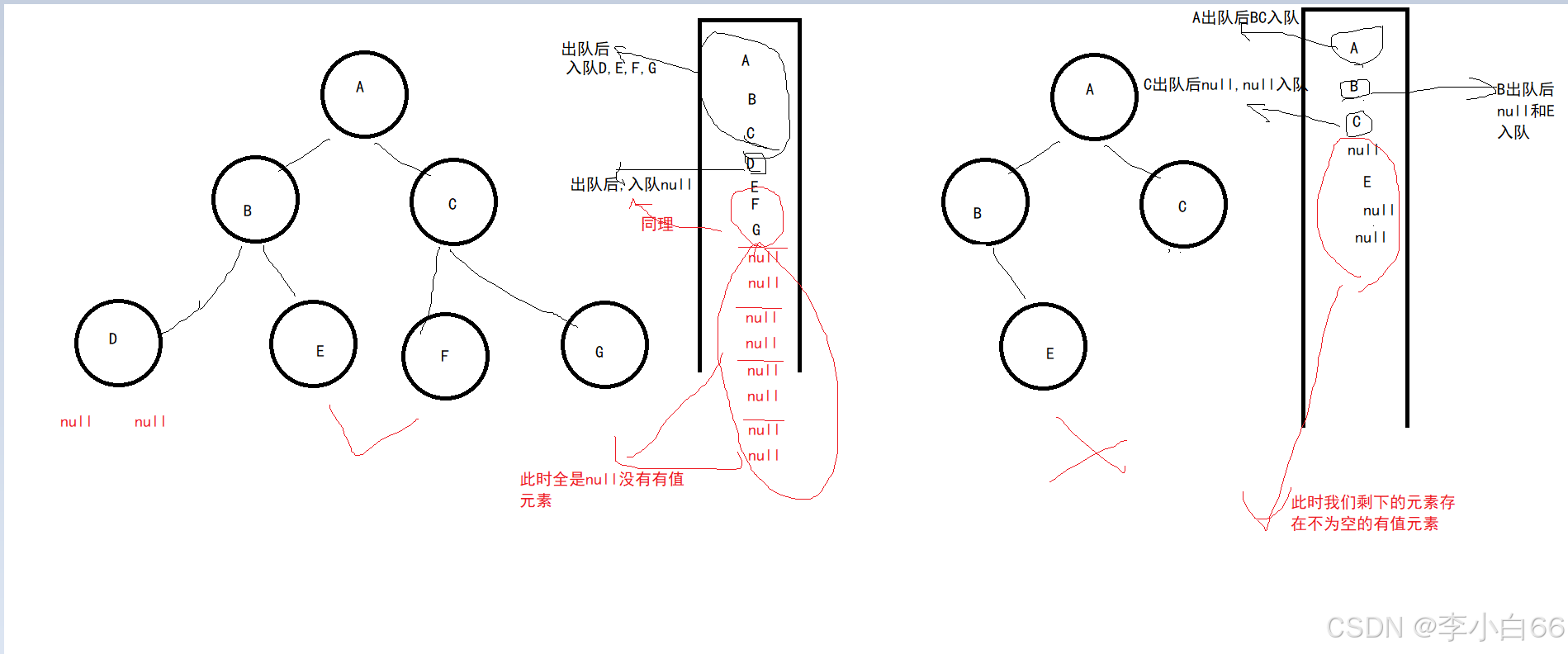
此时,我们需要借助二叉树的层序遍历来进行判断,如图所示
注意,我们队列如果给的是一个null,里面isEmpty判断队列是不为空的.因为有一个null值的元素
具体代码:
//判断一棵树是不是完全二叉树
boolean isCompleteTree(TreeNode root) {
//如果这棵树为空,则是
if(root == null){
return true;
}
//创建队列
Queue<TreeNode> queue = new LinkedList<>();
//进行线序遍历,我们先把根结点加入进去
queue.offer(root);
while (!queue.isEmpty()) {
//取出根结点
TreeNode cur = queue.poll();
if(cur != null){
//不判断左右是否为空直接把左右结点放进去就完事
queue.offer(cur.left);
queue.offer(cur.right);
}else {
//如果当前是null值,我们如果再对cur进行左右结点的操作就会空指针异常
break;
}
}
//此刻判断队列里面是否只剩null
//此刻判断队列里面是否只剩null
while (!queue.isEmpty()) {
if(queue.poll()!=null){
return false;
}else {
continue;
}
}
return true;
}5. 二叉树的构建及遍历
题目解析:
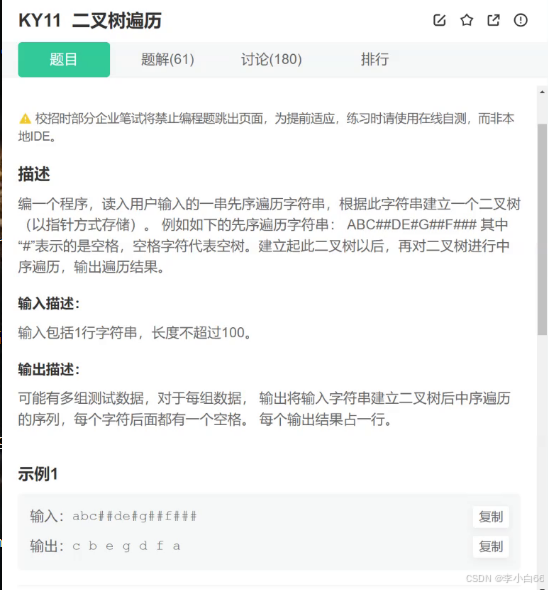
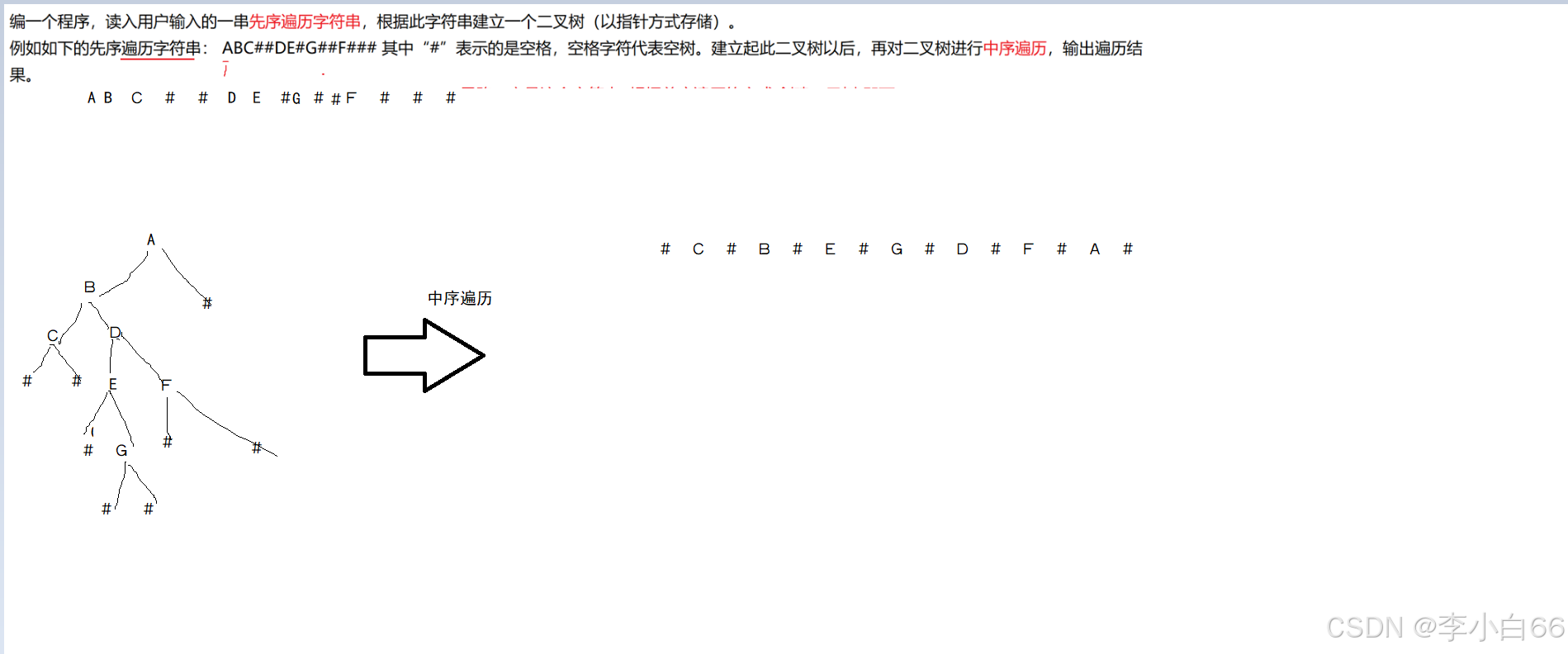
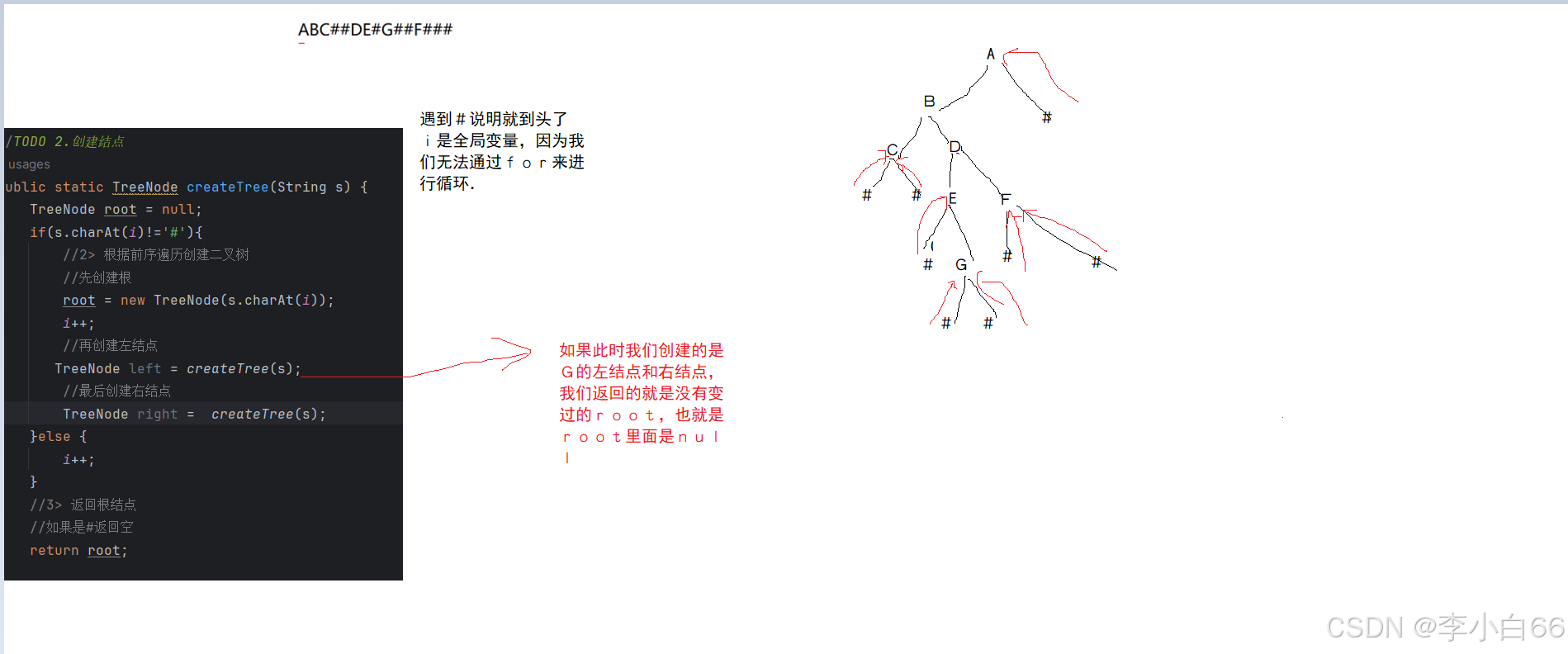
题目: 我们根据二叉树的先序遍历来构造出二叉树,然后输出二叉树的中序遍历
#代表的是空格
第一步:
我们先写出结点的内部类,并且提供构造方法
第二步:
根据给定的字符创建二叉树
第三步:
输出中序遍历的结果
具体代码:
//根据前序遍历构造二叉树,然后输出它的后续遍历
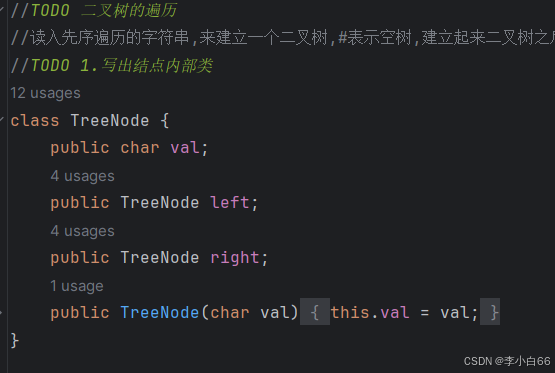
//TODO 1.我们首先创建结点内部类
class TreeNode {
char val;
TreeNode leftTree;
TreeNode rightTree;
public TreeNode(char val) {
this.val = val;
}
}
static int i = 0;
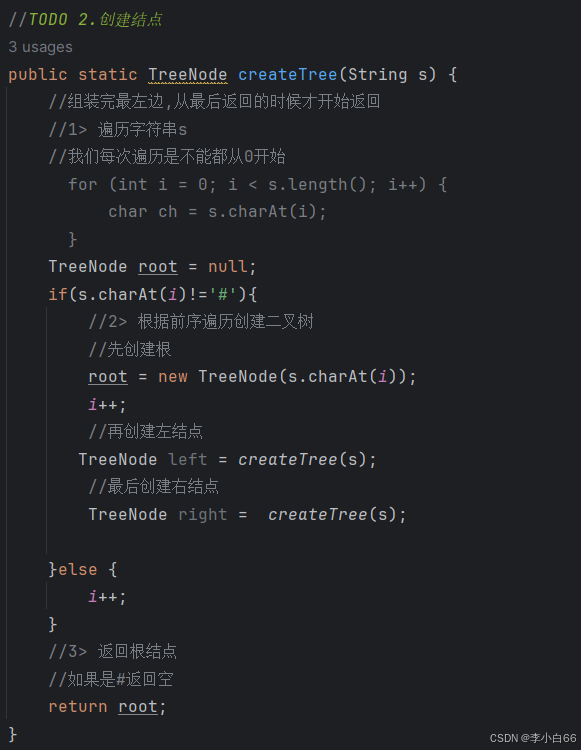
//TODO 2.我们根据给定的字符来创建二叉树
public TreeNode createTree(String s) {
TreeNode node = null;
if(s.charAt(i) != '#'){
//先创建根结点
node = new TreeNode(s.charAt(i));
i++;
//再创建左右子树
//这个就起到一个连接作用
node.leftTree = createTree(s);
node.rightTree = createTree(s);
}else {
i++;
}
return node;
}
//TODO 3. 中序遍历打印二叉树
public static void inorder(TreeNode root) {
if(root == null) {
return;
}
inorder(root.leftTree);
System.out.print(root.val + " ");
inorder(root.rightTree);
}