只需要掌握小题,在考纲中占比不大
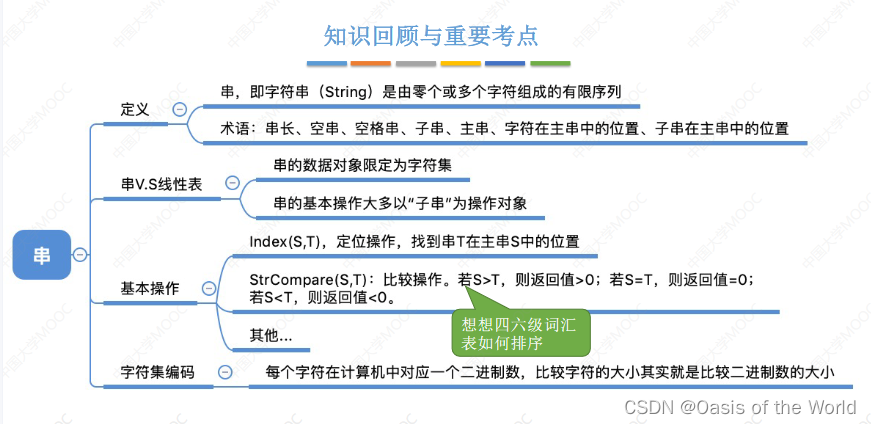
1 串的定义
1.1 基本定义
字符串
数据结构三要数:逻辑结构、存储结构、运算
子串必须是连续的! 空格也是一个字符!每个空格字符占1B
1.2 串和线性表
2 串的基本操作
比值的操作!:就是按照字母表的顺序排列!
只有当两个串完全相同时,才相等!
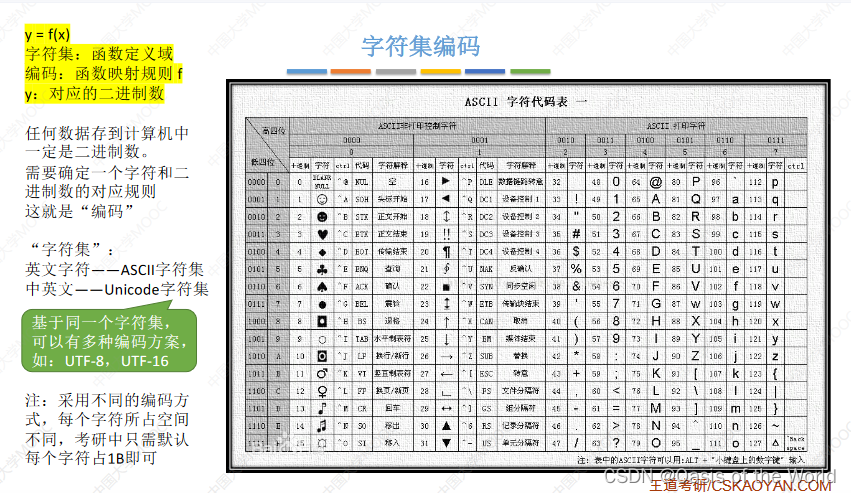
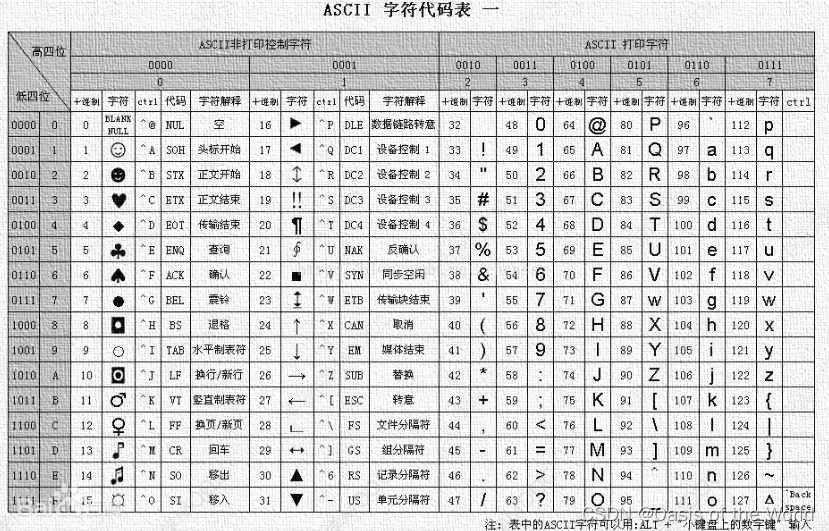
字符串编码表ASCII
a存的是:【高四位】0110【低四位】0001【这样的二进制】
结果就是:
空格这个字符对应的二进制数是:00010000 占8bit位置
一个字母占一个字节1B ,一个字节等于8比特
软件的解码方式出现了错误!
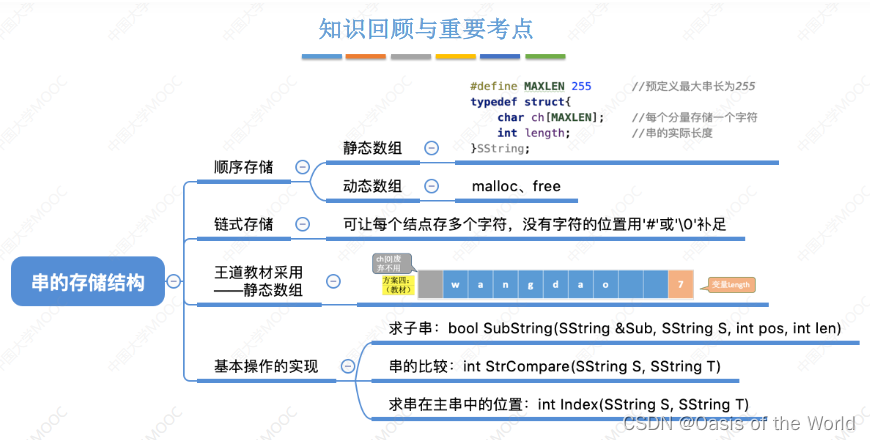
3 串的存储结构
串是特殊的线性表
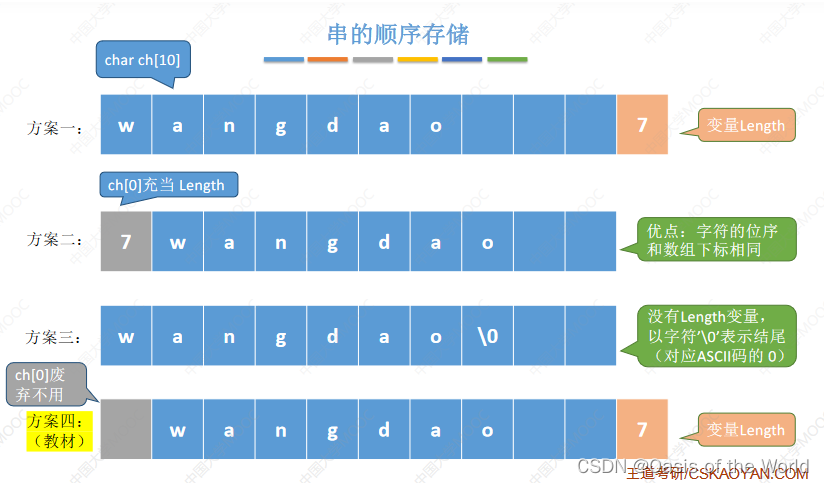
3.1 顺序存储
malloc申请的空间是一个堆区域,堆区的空间需要手动free
优点:随机存取 缺点:插入删除很困难
不同的方案数:
方案二的缺点:char[0]存储的还是一个字节的大小,占8个比特位,也就是说只能表示0到255之间的数字,则字符串的长度不能超过255.
方案四可以有所有的优点!
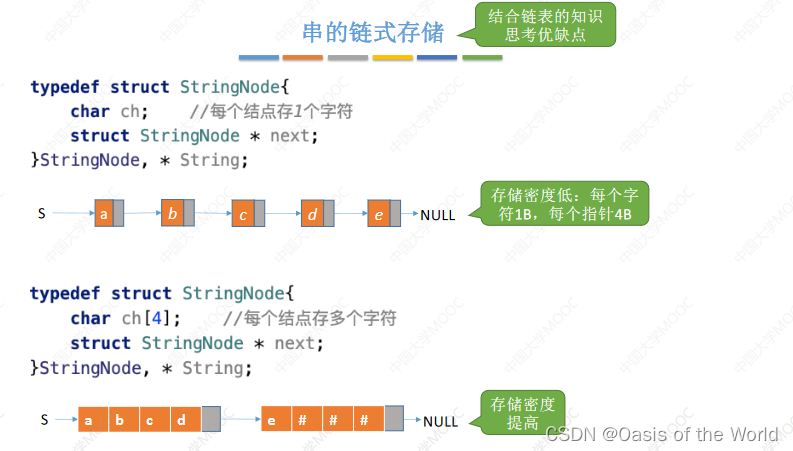
3.2 链式存储
一个字符1B(字节),一个指针4B(字节),这样造成的存储密度低的问题可以通过每个结点存储多个字符解决!!!如果最后一个结点存不满的话就可以用特殊的字符代替,这里式#也可以是/0这样子。
优缺点:增加删除元素很简单但是不具备随机存储的特性!
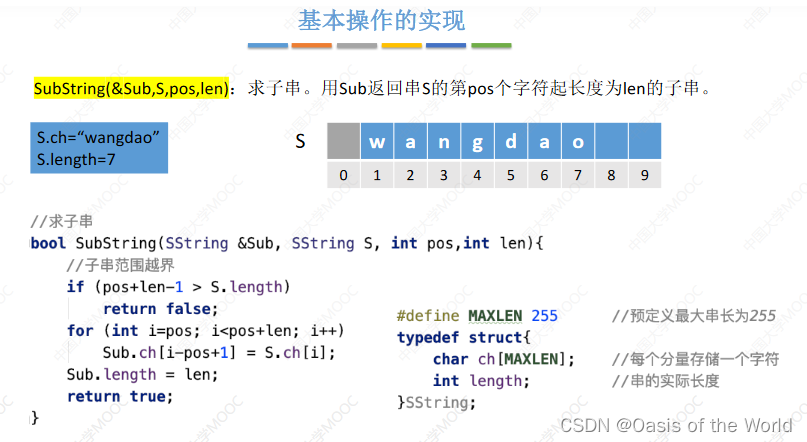
3.2.2 求子串
sub返回内容
3.2.3 比较两个串的大小
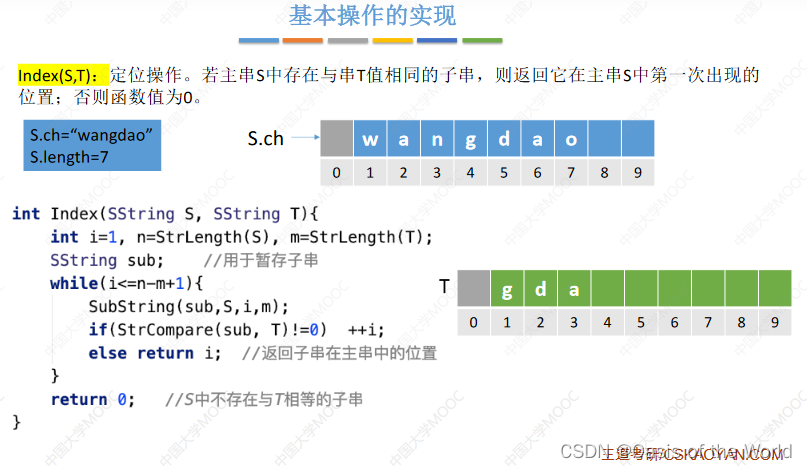
3.2.4 定位操作
一直找新的长度为3的子串!
4 字符串匹配!!!!!!
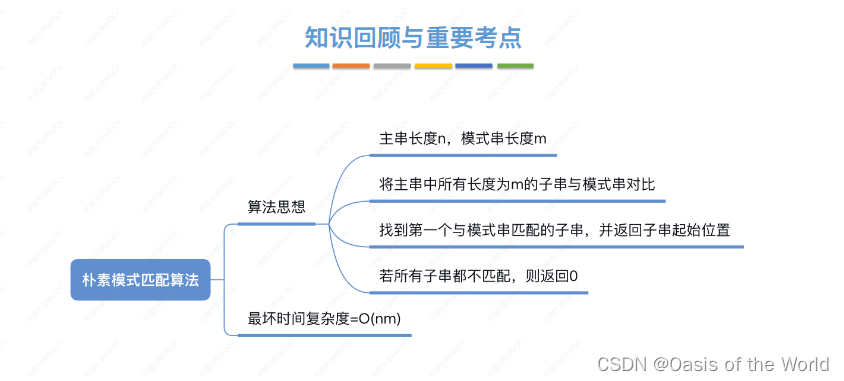
4.1 朴素模式匹配算法
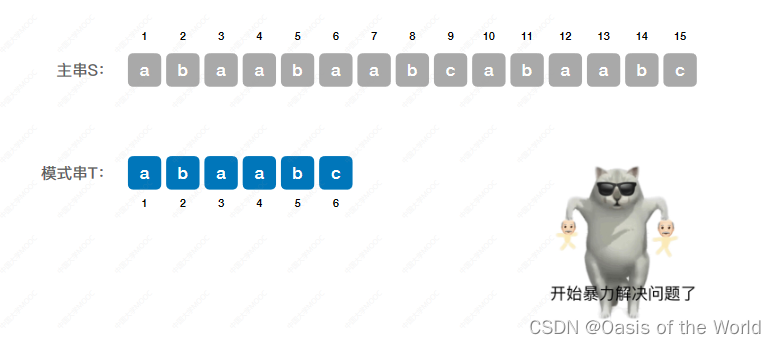
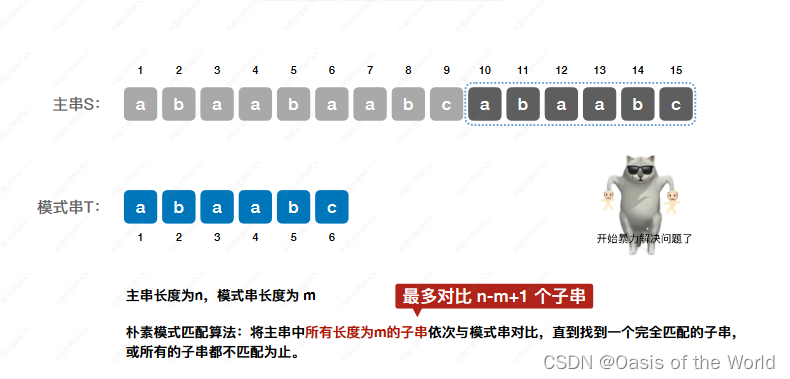
朴素模式匹配算法可以看作是 暴力解决! 思想:找出所有长度为6的子串和模式串对比!
一共有n-m+1个子串,最多对比n-m+1个子串
4.1.1 用index
取子串、对比两个字符串的操作
4.1.2 不使用基本操作
i= i-j+2 i-j会使指针指向这个子串的前面一个位置 +2之后就指向了下一个子串的起始位置!
停止的条件:j>T.length reture i-j+1 或者 i-T.length
代码实现:
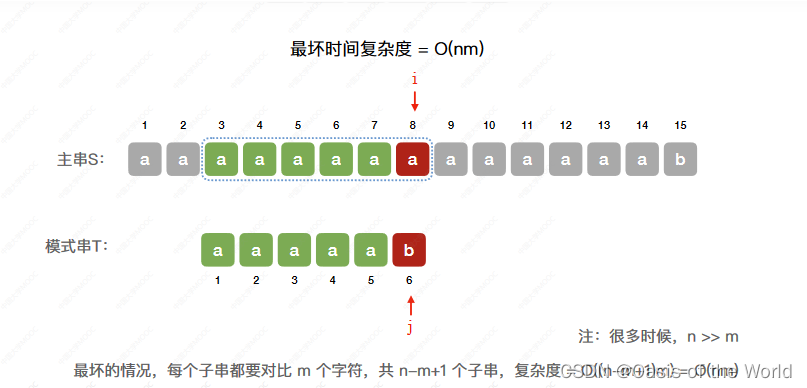
时间复杂度
暴力解法:把所有有可能的都遍历一遍!
前面的都匹配只有最后一个元素不匹配
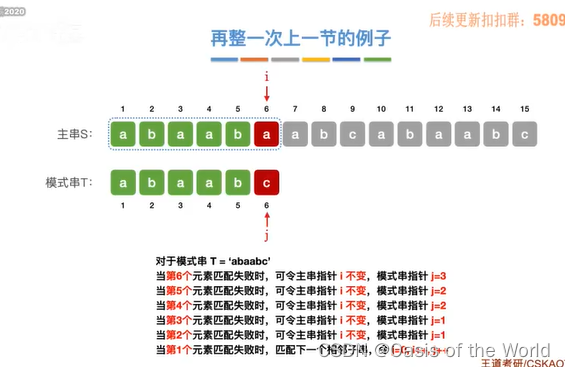
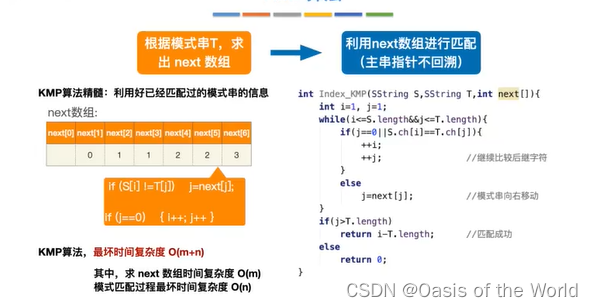
4.2 KMP算法
利用模式串本身的信息 和已经扫描过的信息
当模式串进行失配的时候应该跳到什么样的位置。
所以只要是总结模式串的信息!!!!!
当模式串很短 但是主串很长的时候KMP就会后高效!
可以用数组表示这些信息:当在某个位置发生失配的时候会成什么局面!
在进行匹配之前要对模式串进行预处理得到next数组!!
不需要子串的那个指针变化,只变化模式串的
时间复杂度
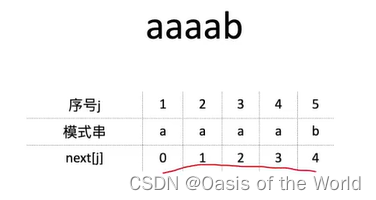
手动的求next数组!!!
求next数组【一】
注意模式串的位序是从1开始的,0表示的是模式串第一个元素的前面一个元素!
1:next【1】=0 在任何的模式串中都一样!
2:next【2】=1在任何的模式串中都一样!
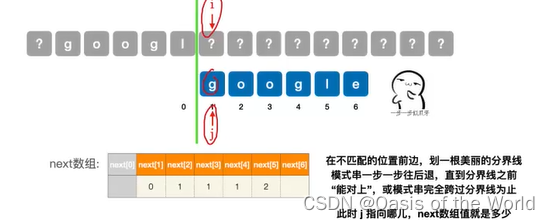
3:其他的画出分界线后 一步一步挪动然后填表!
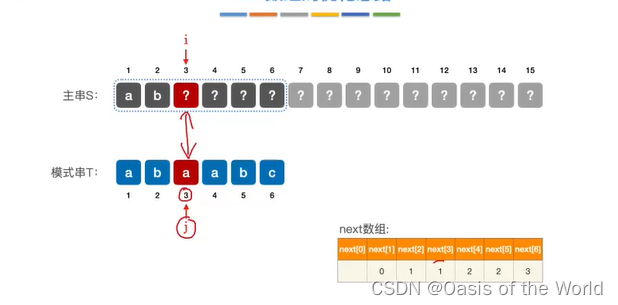
使用next数组:
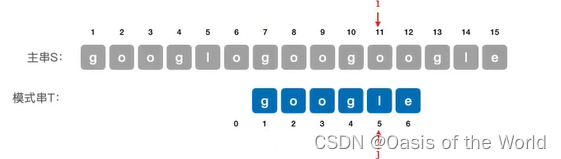
过程:
1:i=6 j=6 不匹配 j = next[6]=1
2:i=6 j=1 不匹配 j = next[1] = 0
3:j=0时特殊处理》》j++,i++
4:i=7 j=1 匹配成功
5:i = 11 j=5 不匹配 j = next[5] = 2
6:i=11,j=2 匹配成功
自己算一下
KMP算法的进一步优化
对next数组进行优化!变成nextval数组!!!逻辑没有改变!
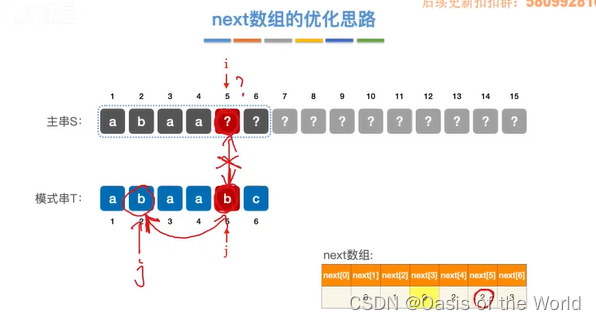
优化思路:
可以直接将next[3]=0
因为此时i的位置一定不是a 所以一定和j=1不匹配,因此直接将指针置为0
next[5]=1 但并不是所有的next数组都可以进行优化!
思路:看失配的字符和所指的字符是否相等,如果相等的话没必要再回到这个位置了,直接回到这个位置的前一个位置即可!!!!
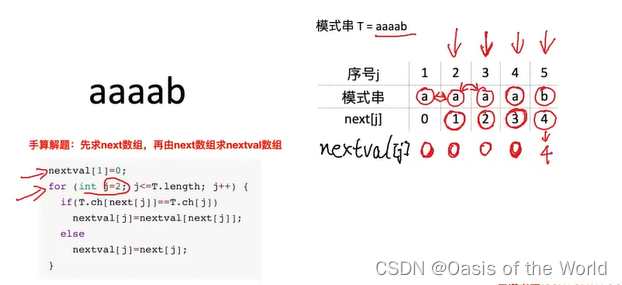
通过next数组求nextval数组
next[1]无脑写0
直接跳到后一步就可以!
nextval【j】 = nextval【next【j】】