校验位：供数据的使用者用来检测数据是否出错的数据，也叫冗余位 。

        数据校验的基本思路：数据的提供者利用数据位根据某种规则生成校验位，将数据位连通校 验位一起提供给使用者。使用者利用收到的可能出错的数据位按照同样的规则生成新的校验位，然后将自己生成的校验位和收到的校验位作比较，从而确定数据位是否有错。（根据同样的数据位，生成校验位，使用者根据自己推测出的校验位和提供者提供的校验位作对比，判断数据是否有误，当使用者推算出的校验位和数据提供者提供的相同，则认为数据并没有出错。反之，则认为提供的数据由于某些因素而出错。）

2，奇偶校验码：

        基本原理：在数据位后面加一位校验位，使得数据位和校验位中：共含偶数个‘1’，称为偶校验，或者共含奇数个‘1’，称为奇校验。

        例如：数据位1011011，采用偶校验，由于数据位含有5个‘1’，所以需要在校验位选择1，组成6个（偶数个）1。数据位连同校验位一起为10110111。如果采用奇校验，那么校验位应该选择0。

        特点：只能检测奇数位错，也无法纠错。（如果有偶数位错，那么校验码和无错的结果是一样的，而且无法判定是1,3还是5位错，只能粗略的判断是奇数位错误）。

3，汉明码：

        汉明码是在分组奇偶校验码的基础上发明的一种用于数据校验的编码方式，由于它可以检测并纠正一位错，所以也叫做汉明纠错码。

1，汉明纠错码的编码规则：

1. 将整个码字（含有数据位和校验位）从左到右从1开始编号：
2. 将所有编号为2的整数次幂的位标记位奇偶校验位，其他剩余位置用作数据位：
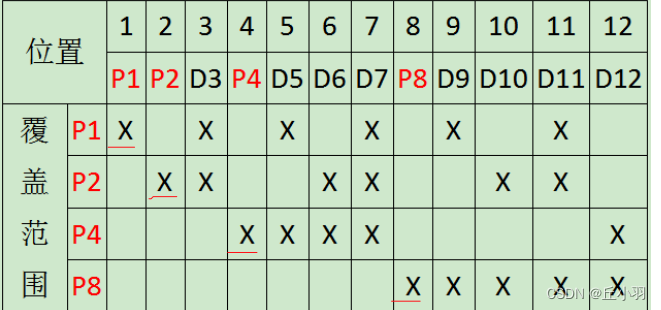
3. 奇偶校验位的位置决定了其负责校验的数据位范围：

P1：用于校验2进制形式编号右起第一位为1的数据位，在表中为所有奇数。

P2:  用于校验2进制形式编号右起第二位为1的数据位。

P4：用于校验2进制形式编号右起第三位为1的数据位。

P8：用于校验2进制形式编号右起第四位为1的数据位。

        总之，Pi负责校验2进制形式编号右起第（logi）+1的数据位。

        结果是每个数据位至少被两个校验位覆盖。如图所示：

     4.将要校验的数据位依次插入数据位，根据数据位进行设置奇偶校验位，对各组数据进行奇偶校验编码，得到整个码字。

        例如：设要校验的数据是10110101，采用偶校验，则其汉明码的产生规则如下：

1. 将要校验的数据10110101依次插入码字格式的数据位：
2. 根据各校验位的校验范围设置校验位：先来看P1:（对应的校验范围是奇数），P2，P4同理  
3. 上图依次对应的是P1，P2，P4，P8的校验位填写，首先来分析P1，由于D3D5D7D9D11为10100，共有偶数个1，而P1作为偶校验码，则P1为0。再来分析P2,P2开始数，隔两个数两个，则码字为P2D3D6D7D10D11，由于D3D6D7D10D11为11110，一共有偶数个1，采用偶校验码，所以P2为0，P4,P8同理。
4. 数据10110101的汉明码是001101100101，写成数据位+校验位的形式是：101101010010。

2，汉明纠错码的校验规则：

1. 根据每个校验位负责校验的数据检查校验位的正确性。
2. 根据出错的校验位决定出错的位置。出错位置=出错校验位的位置之和。

例如：如果校验位P1，P4出错，则出错位置是1+4=5，即第五位有误。

1. 检查各校验位的正确性：

• 先看P1，由于奇数位为010101，显然有奇数个1，所以P1出错。或者可以理解为要根据数据D3D5D7D9D11写P1，而D3D5D7D9D11是10101，有奇数个1，所以按理来说P1应该为1，但是P1却是0，所以P1出错。
• 再来看P2:出错，P2有误。
• 接着看P4：正确。
• 最后看P8:错误，P8出错。

    2.出错的校验位是P1，P2，P8。所以出错的位置是：1+2+8=11，即码字中第11位有错。

        上述例子是用4个校验位对8个数据进行校验，实际上，4个校验位最多可以接受校验11个数据位。一般的，设校验位为k，数据位为n，为了检测并纠正1位错，k和n必须满足这就说明，n最大是-k-1。

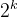
3，汉明纠错码的改进方案：

        汉明码在增加1位校验位后也可以纠正1位错并检测2位错，称为SEC/DED技术。

        增加的一个校验位用于整个码字的校验，其编码规则一如既往，校验时可能出现以下四种情况：

1. 所有的校验位都正确，说明没有错。
2. 增加的校验位正确但是其他校验位错误，说明出现两位错。
3. 增加的校验位有错但是其他校验位正确，说明增加的校验位出错。
4. 增加的校验位有错，其他校验位也有错（某个，某些或全部），说明出现一位可以纠正的错误。