引言
在计算机科学中,递推是一种基本的算法设计技术,它通过将问题分解为更小的子问题来解决。递推法通常用于求解那些可以表示为一系列步骤,并且每个步骤的解依赖于前一步或几步结果的问题。在C++中,递推法的实现可以非常高效,尤其是在处理数学问题和算法设计时。
递推法的定义
递推法是一种通过已知条件逐步推导出结果的算法。它依赖于问题的一个或多个初始条件,然后逐步应用递推关系来计算后续的值。递推法的关键在于递推公式,它描述了如何从已知值计算出新的值。
递推与递归的区别
递推法与递归算法在概念上相似,但实现方式不同。递归是一种通过函数自己调用自己来解决问题的方法,而递推则是通过迭代的方式逐步解决问题。递推通常使用循环结构实现,而递归则需要函数调用栈的支持。
递推法的应用场景
递推法在多种场景下都有应用,包括但不限于:
- 数学问题,如斐波那契数列、阶乘计算等。
- 动态规划问题,递推是动态规划算法的核心思想。
- 组合数学问题,如组合、排列的计算。
- 算法设计,如某些排序算法、搜索算法等。
斐波那契数列的递推实现
斐波那契数列是一个经典的递推问题,其递推公式为:,其中
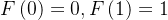
#include <iostream>
int fibonacci(int n) {
if (n <= 1) {
return n;
}
int first = 0, second = 1;
for (int i = 2; i <= n; ++i) {
int next = first + second;
first = second;
second = next;
}
return second;
}
int main() {
int n = 10;
std::cout << "Fibonacci of " << n << " is " << fibonacci(n) << std::endl;
return 0;
}动态规划中的递推
动态规划是一种通过将复杂问题分解为更简单的子问题来求解的方法。在动态规划中,递推法被用来填充一个表格,每个表格项的值都是基于之前计算出的值。
0/1背包问题
0/1背包问题是动态规划的经典问题之一。问题描述如下:给定一组物品,每个物品都有一个重量和一个价值,确定最多能携带的物品数量,使得总重量不超过背包的容量,同时总价值最大。
#include <vector>
#include <iostream>
int knapsack(int W, std::vector<int>& weights, std::vector<int>& values, int n) {
std::vector<std::vector<int>> dp(n+1, std::vector<int>(W+1, 0));
for (int i = 1; i <= n; ++i) {
for (int w = 1; w <= W; ++w) {
if (weights[i-1] <= w) {
dp[i][w] = std::max(dp[i-1][w], values[i-1] + dp[i-1][w-weights[i-1]]);
} else {
dp[i][w] = dp[i-1][w];
}
}
}
return dp[n][W];
}
int main() {
int n = 4, W = 7;
std::vector<int> values = {60, 100, 120, 240};
std::vector<int> weights = {10, 20, 30, 50};
std::cout << "Maximum value: " << knapsack(W, weights, values, n) << std::endl;
return 0;
}结语
递推法是一种强大的算法设计技术,它在解决许多问题时都发挥着关键作用。在C++中,递推法的实现通常需要对问题有深入的理解,以及对递推关系和边界条件的准确把握。