目录
前言:为了学习map和set,需要先学二叉搜索树作为铺垫。
一、二叉搜索树的概念
二叉搜索树是一棵二叉树,又称为二叉排序树,它有以下特性:
1.若左子树不为空,则左子树的节点值比根要小
2.若右子树不为空,则右子树的节点值比根要大
3.整棵树都遵循以上规则
需要注意,二叉树也可以是空树。
二、二叉搜索树的操作
2.1插入
插入的思路是,先用递归将树搜索一遍,用key和树的根的节点比大小,比它大往右走,比它小往左走,直到走到空,那么就在空的位置插入。
2.2删除
删除的思路比较复杂。删除情况分三种,分别是所要删除的节点情况,若删除的是key节点:
1.有左子树,无右子树
这里就将key节点的前一个节点,指向它的后一个节点,然后释放key节点。
2.有右子树,无左子树
和上面类似。
3.有左子树和右子树
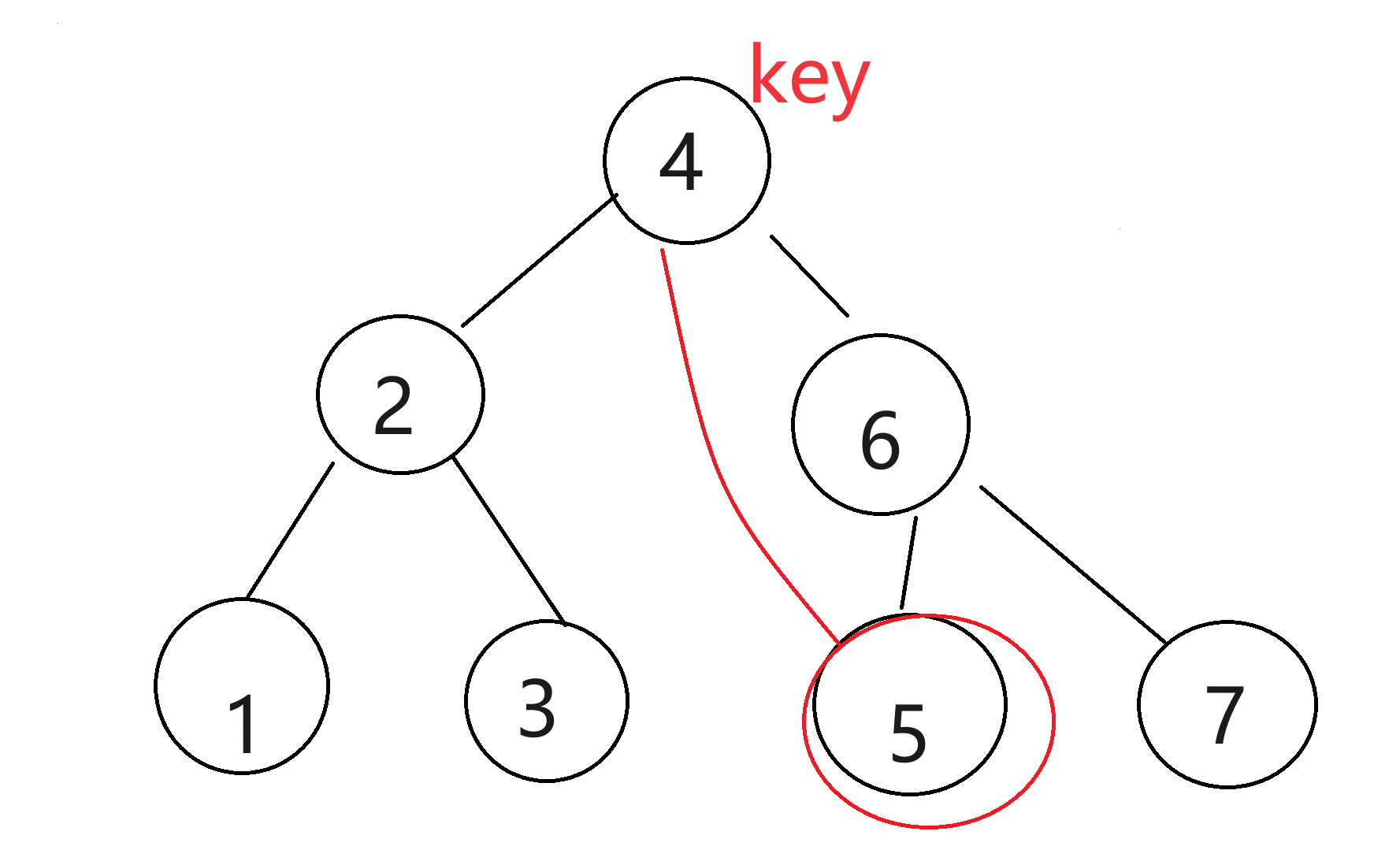
这里比较复杂,需要将key节点与它的左子树中的最大的一个,或者右子树中最小的一个交换,然后再删除key。
右子树中最小的一个,是第一个右节点的最左的节点。若没有最左节点,那就只能和右节点交换。
交换以后,就可以删除key节点也就是4了。
最后一种无左子树也无右子树可以放在1和2中讨论,归为一种。操作比较简单,此处不再赘述。
三、二叉搜索树的实现
要点
1.为了体现封装,我们只留接口放在类的public中,把具体实现的细节放在private中,这样也方便代码日后维护。同时由于使用递归,所以需要取root的引用,参数就要给root,而在类外是没有办法获取作为私有的root的,因此只能把实现的细节写在private里。
2.搜索二叉树可以用来匹配,比如说当字典使用和门禁系统,这里可以再放入一个类模板。
3.插入的时候要新建一个节点再插入,这里会改变root的地址,所以传引用会更好,不然就要传二级指针了,这个很麻烦,而且在C++中是避免的。
4.删除的时候,要先找到这个节点,再删除。删除时,一共涉及三个指针的操作。建议先理清思路再写代码。
namespace ting
{
template<class K, class V>
struct BSTreeNode
{
BSTreeNode(const K& content, const V& value)
:_content(content)
,_left(nullptr)
,_right(nullptr)
,_value(value)
{
}
K _content;
BSTreeNode<K,V>* _left;
BSTreeNode<K,V>* _right;
V _value;
};
template<class K, class V>
class BSTree
{
typedef BSTreeNode<K, V> Node;
public:
bool Insert(const K& key, const V& value)
{
return _Insert(_root, key, value);
}
Node* Find(const K& key)
{
return _Find(_root, key);
}
bool Erase(const K& key)
{
return _Erase(_root, key);
}
void InOrder()
{
_InOrder(_root);
}
private:
Node* _root = nullptr;
Node* _Find(Node* root, const K& key)
{
while (root != nullptr)
{
if (root->_content < key)
{
root = root->_right;
}
else if (root->_content > key)
{
root = root->_left;
}
else if (root->_content == key)
{
return root;
}
}
return nullptr;
}
void _InOrder(Node* root)
{
if (root == nullptr)
return;
_InOrder(root->_left);
cout << root->_content<<" "<<root->_value << endl;
_InOrder(root->_right);
}
bool _Insert(Node*& root, const K& key, const V& value)
{
if (root == nullptr)
{
/*root->_content = key;
root->_value = value;
return true;*/
root = new Node(key, value);//这里要给root建一个节点
return true;
}
if (root->_content < key)
{
return _Insert(root->_right, key, value);
}
else if (root->_content > key)
{
return _Insert(root->_left, key, value);
}
else
{
return false;
}
}
bool _Erase(Node*& root, const K& key)
{
if (root == nullptr)
return false;
if (root->_content < key)
{
return _Erase(root->_right, key);
}
else if (root->_content > key)
{
return _Erase(root->_left, key);
}
else
{
Node* del = root;
if (root->_left == nullptr)
{
root = root->_right;
}
else if (root->_right == nullptr)
{
root = root->_left;
}
else
{
Node* prev = root;
Node* minNode = root->_right;
while (minNode->_left != nullptr)
{
prev = minNode;
minNode = minNode->_left;
}
root->_content = minNode->_content;
root->_value = minNode->_value;
if (prev->_left == minNode)
{
prev->_left = minNode->_right;
}
else
{
prev->_right = minNode->_right;
}
del = minNode;
}
delete del;
return true;
}
}
};
void TestBSTree()
{
BSTree<string, string> dict;
dict.Insert("insert", "插入");
dict.Insert("erase", "删除");
dict.Insert("left", "左边");
dict.Insert("string", "字符串");
string str;
while (cin >> str)
{
auto ret = dict.Find(str);
if (ret)
{
cout << str << ":" << ret->_value << endl;
}
else
{
cout << "单词拼写错误" << endl;
}
}
string strs[] = { "苹果", "西瓜", "苹果", "樱桃", "苹果", "樱桃", "苹果", "樱桃", "苹果" };
// 统计水果出现的次
BSTree<string, int> countTree;
for (auto str : strs)
{
auto ret = countTree.Find(str);
if (ret == NULL)
{
countTree.Insert(str, 1);
}
else
{
ret->_value++;
}
}
countTree.InOrder();
}
}