任务分配问题（回溯法）

一、问题叙述

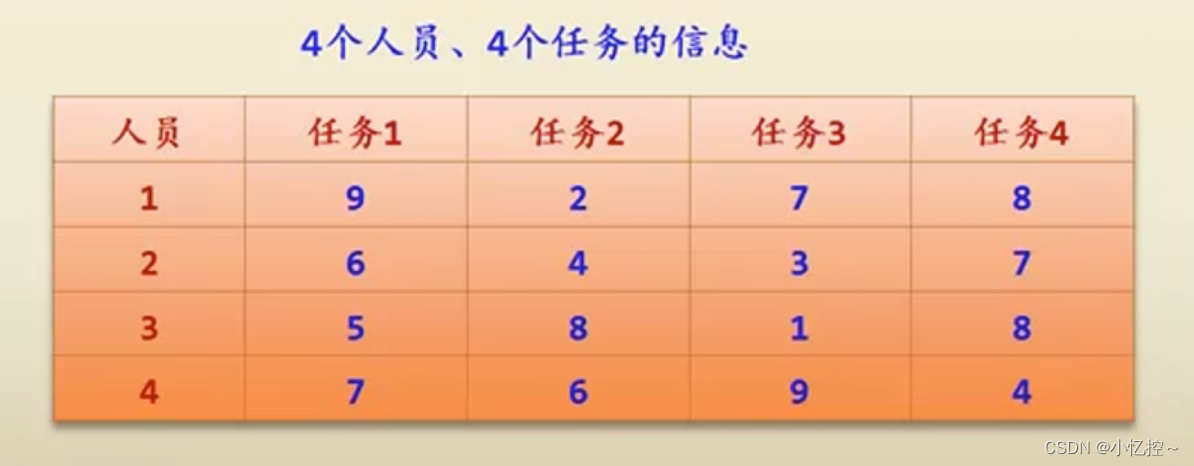
【问题描述】有n (n>=1)个任务需要分配给 n个人执行,每个任务只能分配给一个人,每个人只能执行一个任务。第i个人执行第j个任务的成本是c [i] [j](1≤i,j≤n)。求出总成本最小的分配方案。

二、示例分析

任务分配问题是一个经典的组合优化问题，也可以称为工人任务分配问题或者是最优匹配问题。在任务分配问题中，有n个任务和m个工人，每个任务只能由一个工人完成，并且每个工人只能完成一个任务。每个任务有一个完成该任务所需的时间，每个工人有一个完成任务的效率。任务分配问题的目标是找到一个最优的任务分配方案，使得所有任务完成的总时间最短。回溯法是一种解决组合优化问题的有效方法。在任务分配问题中，我们可以按照一定的规则逐步地尝试将任务分配给工人，直到所有任务都被分配完毕。如果在某一步无法找到合适的工人来完成任务，那么就回溯到上一步，尝试其他的分配方案。通过不断地回溯和尝试，最终可以找到一个最优的任务分配方案。

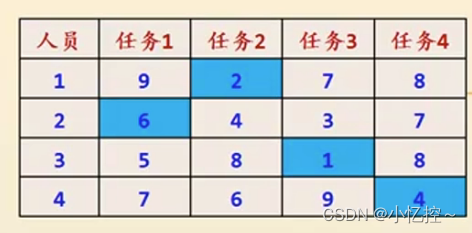
根据回溯法可以得到结果如下:

三、解题思路

回溯法解题的一般步骤
（1）针对给定的问题确定问题的解空间树，问题的解空间树应至少包含问题的一个解或者最优解。
（2）确定结点的扩展搜索规则
（3）以深度优先的方式搜索解空间树，并在搜索的过程中可以采用减枝函数来避免无效搜索。其中，深度优先方式可以选择递归回溯或者迭代（非递归）回溯

通过将问题进行适当的转化，得出解空间树为排列树，这棵树每条完整路径都代表了一种解的可能。通过深度优先搜索这棵树，枚举每种可能的解的情况，找出能得到最小的花费结果。其中构造约束函数，可以删除一些不可能的解，从而大大提高程序效率

四、代码实现：

#include <stdio.h>

#define NUM_TASKS 4
#define NUM_WORKERS 4

int min_time = 9999; // 记录最优时间

void backtrack(int tasks[][NUM_TASKS], int workers[], int assignments[], int current_time) {
    // 检查当前时间是否超过当前最优时间，如果是则直接返回
    if (current_time >= min_time) {
        return;
    }

    // 如果所有任务都被分配完，更新最优时间并返回
    int i;
    for (i = 0; i < NUM_TASKS; i++) {
        if (assignments[i] == -1) break;
    }
    if (i == NUM_TASKS) {
        min_time = current_time;
        return;
    }

    // 递归尝试将任务分配给每个工人
    for (i = 0; i < NUM_WORKERS; i++) {
        if (assignments[i] == -1) {
            // 分配任务
            assignments[i] = tasks[i][NUM_TASKS - 1 - current_time];
            int new_time = current_time + tasks[i][NUM_TASKS - 1 - current_time];

            // 递归调用
            backtrack(tasks, workers, assignments, new_time);

            // 回溯
            assignments[i] = -1;
        }
    }
}

int main() {
    int tasks[NUM_WORKERS][NUM_TASKS] = {
        {9, 2, 7, 8},
        {6, 4, 3, 7},
        {5, 8, 1, 8},
        {7, 6, 9, 4}
    };
    int workers[NUM_WORKERS] = {1, 2, 3, 4};
    int assignments[NUM_WORKERS];
    
    // 初始化任务分配情况
    for (int i = 0; i < NUM_WORKERS; i++) {
        assignments[i] = -1;
    }

    // 调用回溯函数
    backtrack(tasks, workers, assignments, 0);

    // 输出最优时间
    printf("最优时间：%d\n", min_time);

    return 0;
}

结果如下：12 是最短时间效率，前面的字是Clion 没有识别出来

总结

回溯法对任务分配问题：

优点：
1. 能够找到最优解：回溯法可以尝试所有可能的任务分配方案，从中找到总时间最短的最优解。
2. 灵活性强：通过回溯法，可以灵活地适应不同的任务分配情况，并尝试各种组合。
3. 相对简单：在一些情况下，回溯法是一种相对简单直观的解决方法。

缺点：
1. 时间复杂度高：由于回溯法会尝试所有可能的分配方案，对于大规模任务分配问题，可能需要消耗大量的计算时间。
2. 空间复杂度高：递归调用会占用大量的栈空间，特别是在问题规模较大时容易导致栈溢出问题。
3. 可能不适用于大规模问题：对于任务数量较多或工人数量较多的大规模任务分配问题，回溯法可能不是最优选择。

总的来说，回溯法在任务分配问题中可以找到最优解，但在时间和空间复杂度上的限制可能使其不适用于大规模问题。在实际应用中，可以根据具体情况选择合适的算法来解决任务分配问题。