导入
从今天开始正式讲解数据结构中的内容。由于本人以前学过一些数据结构的知识,所以就先直接讲解一些题目。关于链表等数据结构的实现的文章将会在后面进行发布
今天这篇文章主要是分享两道有意思的题目:
1.带环的链表的判断、返回链表环的起点
这部分内容十分经典且需要一些数学知识进行推导,本文将重点对这个部分的数学知识推导以及代码实现进行一个讲解
2.随机链表的复制(深拷贝)
这个部分对单向不循环链表的操作是有要求的。可以很好地检验对链表操作的代码编写能力。同时考虑了时间复杂度等因素下的对算法的优化。但由于目前只学习到c语言,学习内容并不深,所以文中讲解的方法仅是针对当前进度下的最优办法。
带环链表
何为带环链表
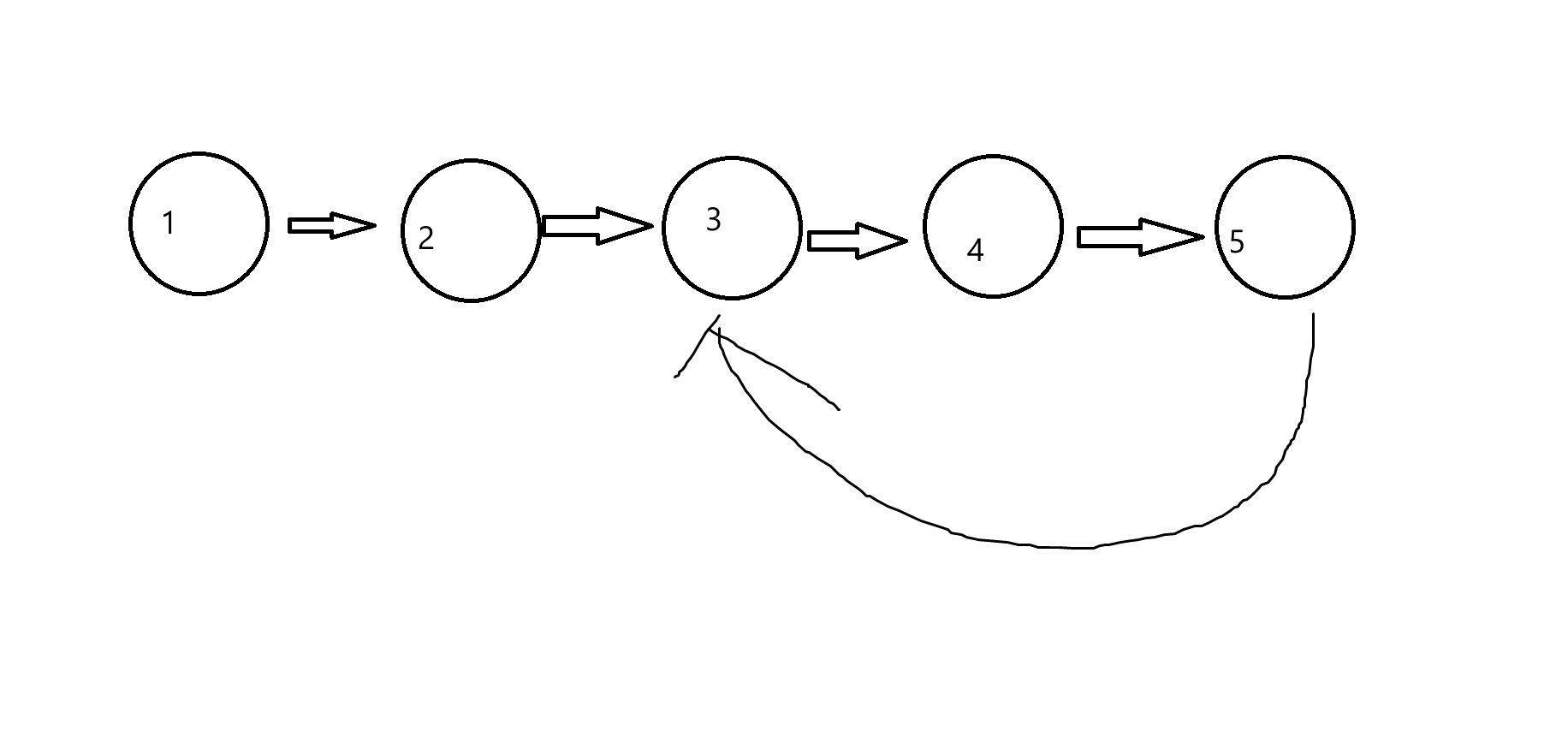
如图所示:
这就是一个经典的带环链表的样子。大致就是,一个链表的最后一个节点,其next指针会指向会到链表前面中的某个节点,当然,包括它自己。所以链表若只有一个元素也是可以成环的。
判断链表是否成环
所以,引出了第一个问题,判断链表是否成环?成环返回ture,反之返回false。
原题:链表中是否有环 Leetcode 141
感兴趣的读者可以前往尝试一下。
这题乍一看,感觉也挺简单,很多人会想:
使用一个指针p,从头开始走,只要不为空就一直往后走不就可以了吗?
但是这个想法是不对的,如果这个链表不成环,那么确实可以,p==NULL的时候直接返回false就可以了。但是如果链表成环了呢?那岂不是一直走不到空,只要进入环内部了就不会再出来,一直不为空。最后会变成死循环。
在这里先给出具体实现方案:
使用快慢指针fast和slow,fast一次走两步,slow一次走一步。如果有环,fast会追击slow,在环中相遇,返回ture。反之返回false。
代码实现:
bool hasCycle(struct ListNode *head) {
struct ListNode* fast=head,*slow=head;
while(fast&&fast->next){
slow=slow->next;
fast=fast->next->next;
if(fast==slow) return true;
}
return false;
}
当然会有小伙伴好奇,这为什么能够判断出来呢?
现在我们来讲述一下原理:
当链表不成环时:
当链表不成环的时候,那么链表最后一个节点指向的肯定是NULL。因为fast一次向后走两次,所以fast一定会比slow先到链表尾部。
但是问题是,由于fast一次走两步,就导致了fast可能走到两个位置。一个是链表最后一个节点,一个是NULL。所以在判断是否继续追击的循环过程中,退出的条件就是上述的两个: fast&&fast->next。若退出该循环了,则表示不成环,返回false。
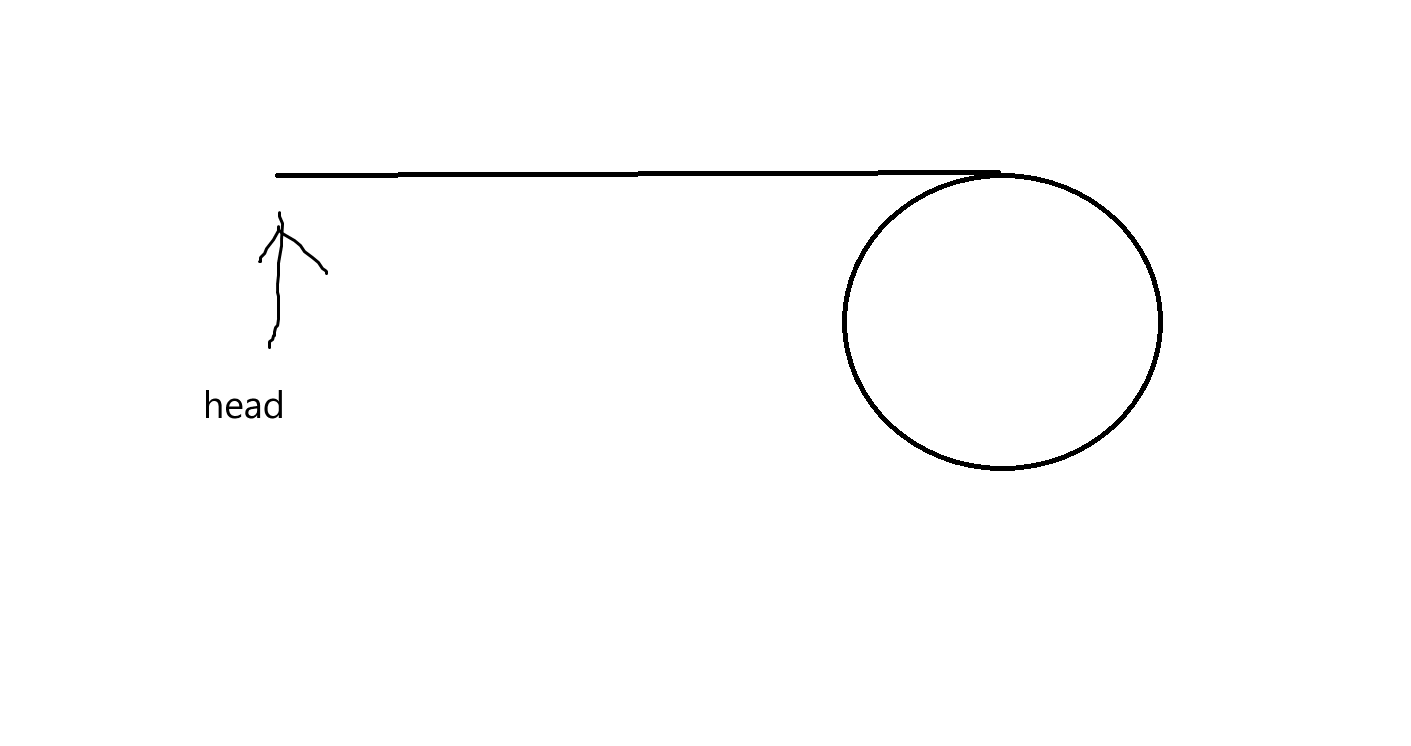
当链表成环时:
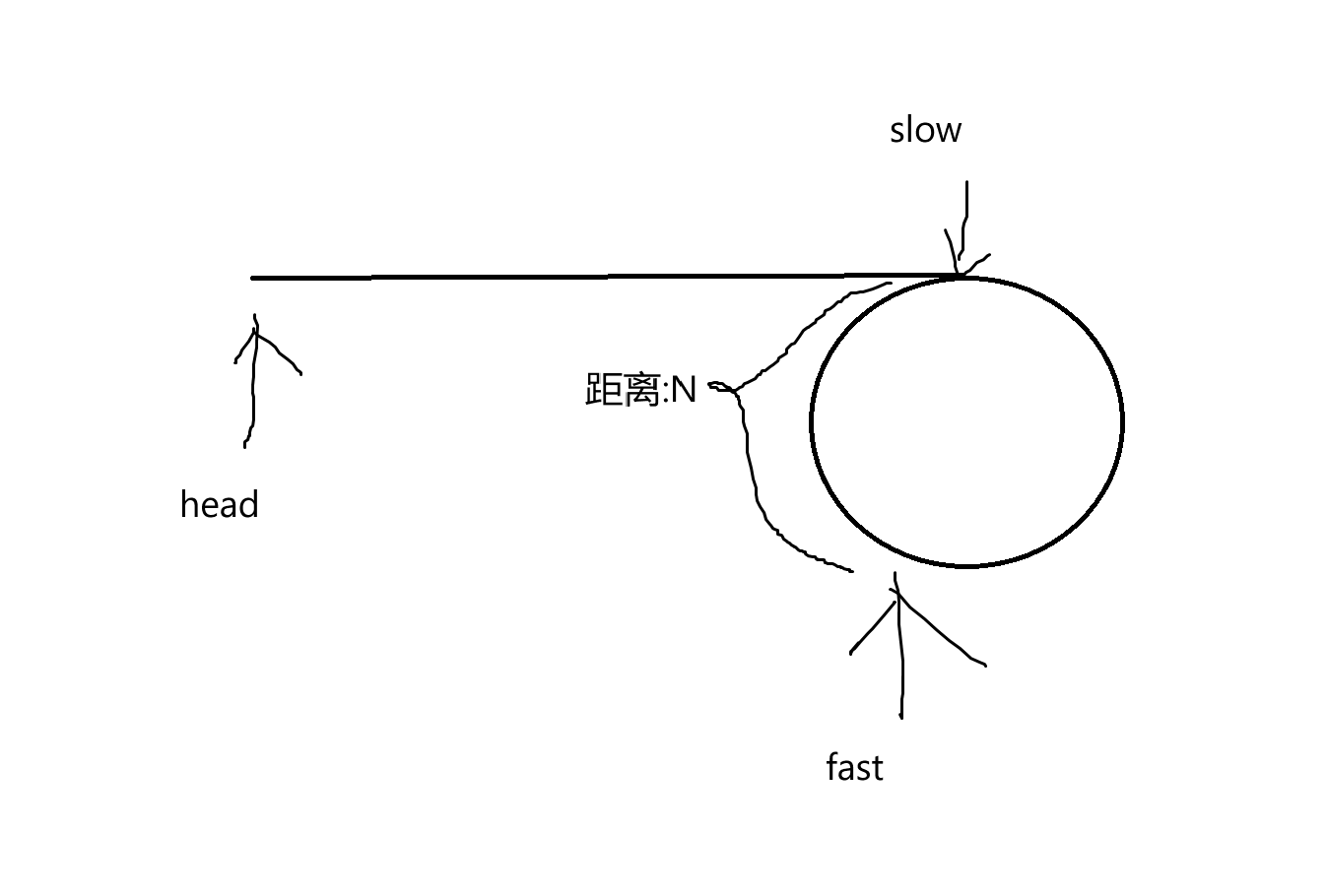
假设这是我们将链表抽象过后的模型,后面的圆圈就是环区。我们知道,成环后,指针会一直在环区内走。假设slow刚好进环的一刻,fast已经在环区内运动一段时间了:
此时,假设fast距离slow的距离是N。
分析:我们知道,fast每次都比slow多走一步,那么也就是说,两个指针每运动一次,距离会减小1。因为进入环后,指针只会在环区内运动,所以两个指针的距离会越来越小直至为0,那么就是相遇上了,就可以判断此时链表一定是成环的,则返回true。
我们来看一下这个算法的时间复杂度和空间复杂度:
时间复杂度:因为从头到尾都只有一个循环在操作,即使fast不断地在环区内转圈,那循环次数地量级也就是一次函数级别的,所以为O(N)。
空间复杂度:为了使用该算法,仅仅额外创建了两个变量,即fast和slow,为常数级别,O(1)。
成环链表算法扩展
看完上面的分析后,可能还是会有疑问,为什么快指针一次走两步呢?难道不能是三步,四步,五步…?对此,下面我们继续分析一下。
就以fast一次走散三步为例子,假设还是刚刚那样,slow刚进环,fast追击slow的距离为N:
那么此时两个指针的步数之差就为3-1=2步,也就是说,每运动一次,距离缩小2。
如果N为偶数,那么当距离为0的时候,就直接追上了。但是N为奇数的时候,追着追着发现距离为-1了,这是什么意思呢?
其实也很好理解,意思就是,fast在第一轮追击后没追成功,fast跑到slow前面一个位置了。我们可以理解为跑步比赛时候的套圈。那么需要继续判断追击是否成功。
我们假设环的长度(即节点个数)为C,那么此时追击的距离变成了C-1。
如果C为偶数,C-1为奇数,那么还得追。反之追得上。
这个时候我们很可能会想,那么如果C为偶数,N为奇数的情况下,那岂不是追不上了?
我们来分析一下:
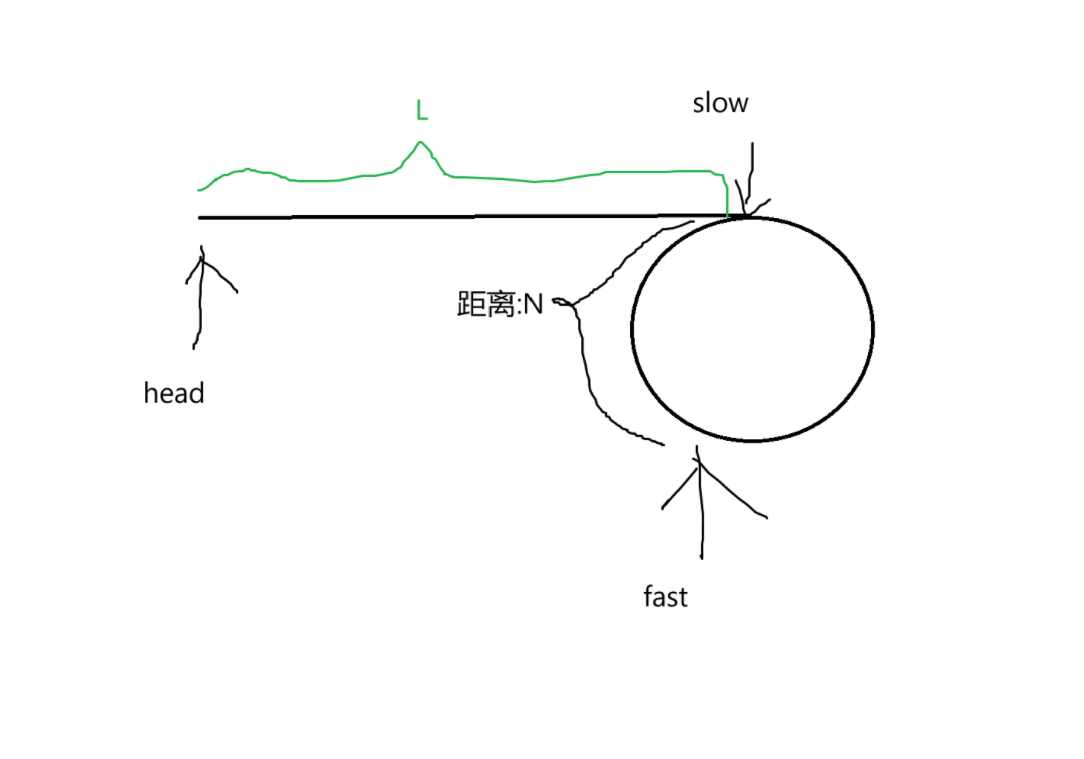
我们得先知道一个关系就是,fast走的距离是slow走的距离的3倍。
假设从链表开头到环第一个节点距离为L:
刚进入环的时候,slow走了L距离,fast走的应该是L+x*C的距离。因为slow还没进环的时候,fast很可能已在里面转了很多圈了。此时fast追击的距离为N。
所以我们此时得到Sslow=L,Sfast=L+x * C+C-N。
根据二者运动关系很容易得到:3 * L=fast=L+x * C+C-N。
得到N与C的关系式:N=(x+1) * C-2 * L
由奇数与偶数的计算规律:
| 数 | 计算方式 | 数 | 结果 |
|---|---|---|---|
| 奇数 | ± | 奇数 | 偶数 |
| 奇数 | ± | 偶数 | 奇数 |
| 偶数 | ± | 偶数 | 偶数 |
| 奇数 | * | 奇数 | 奇数 |
| 奇数 | * | 偶数 | 偶数 |
| 偶数 | * | 偶数 | 偶数 |
我们很容易得知:
当N为偶数的时候,(x+1)*C也是偶数,无论C为偶数还是奇数,都有可能。正好符合我们上面的分析,即N为偶数的时候一定能追上。
而当N为奇数的时候,(x+1)*C一定得是奇数,那么C一定是奇数,而不可能出现C为偶数的情况。
而这个式子是一定成立的,因为它表示了当slow刚进环的时候,fast和slow的位移关系。故我们推出一个结论,不可能出现C为偶数,N为奇数的情况。即一定是追的上的。
而对于fast一次走多少步,我们也是可以一样进行分析的。假设一次走k步。
对于是否为奇数偶数的情况,我们只需改为判断(N%(k-1)==0)或者(N%(k-1)!=0)就可。在这里就不多细讲,只需举多几个例子简单验证就好。
所以我们得到一个结论,一定是追的上的。
返回成环链表的第一个环节点
现在升级一下要求:返回一下环中第一个节点:
要求:给定一个链表,返回链表开始入环的第一个节点。 从链表的头节点开始沿着 next
指针进入环的第一个节点为环的入口节点。如果链表无环,则返回 null。且不允许修改给定的链表。
现在我们知道了如何判断一个链表是否成环的方法,所以只需解决如何找到环中第一个节点。
还是一样的流程,在这里先给出如何操作,然后再来证明为什么:
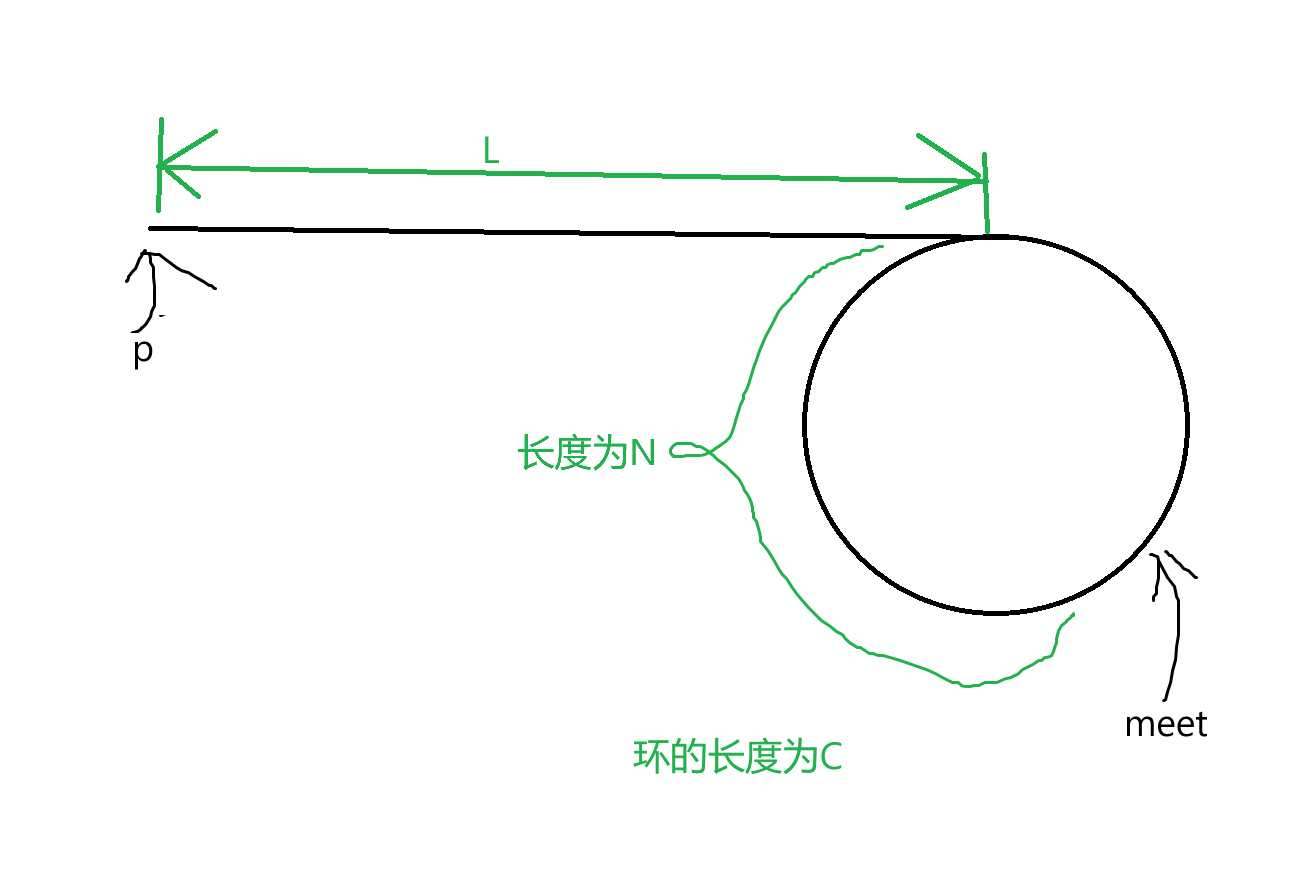
和上面一样,先让fast指针和slow指针先相遇,用指针meet指向相遇的那个节点。然后声名一个指针p从链表的头开始走,meet和p一定会相遇(后续证明),相遇时候的节点就是第一个节点
<font color="blue“>代码实现:
bool hasCycle(struct ListNode *head,struct ListNode** meet) {
struct ListNode* fast=head,*slow=head;
while(fast&&fast->next){
slow=slow->next;
fast=fast->next->next;
if(fast==slow) {
*meet=fast;
return true;
}
}
return false;
}
struct ListNode *detectCycle(struct ListNode *head) {
struct ListNode* meet=NULL;
if(!hasCycle(head,&meet)) return NULL;
//反之一定有环
else{
struct ListNode* p=head;
while(p!=meet){
p=p->next;
meet=meet->next;
}
return p;
}
}
注:在这里对判断是否有环的那个函数进行了改造,目的是为了能找到fast和slow相遇的位置。
这时候就有疑惑了,为什么meet和p指针一起走一定会在环的第一个节点处相遇呢?meet可能会转很多圈啊,难道是巧合?
证明过程如下:
注意此时fast一次走两步,slow一次走一步。
设t=C-N,当fast和slow相遇的时候:
slow走过的距离:L+t
fast走过的距离是L+t+x * C
由关系得知:2 * (L+t)=L+t+x * C
可得:L=x * C-t
由这个等式可以得知什么呢?
当p从头走到环第一个节点时,走的距离是L,这个距离L恰好等于x * C-t这个距离。我们知道,如果在环内走整数倍圈,会走到自己这里。再减t,距离会相较于原来退后t。
meet走L的距离,就相当于走x * C-t这个距离,最后的位置相对现在退后t,即环第一个节点处。所以p和meet同时走L(x * C-t)这段距离,一定刚好在环第一个节点相遇。
在这里还提供一种思路:
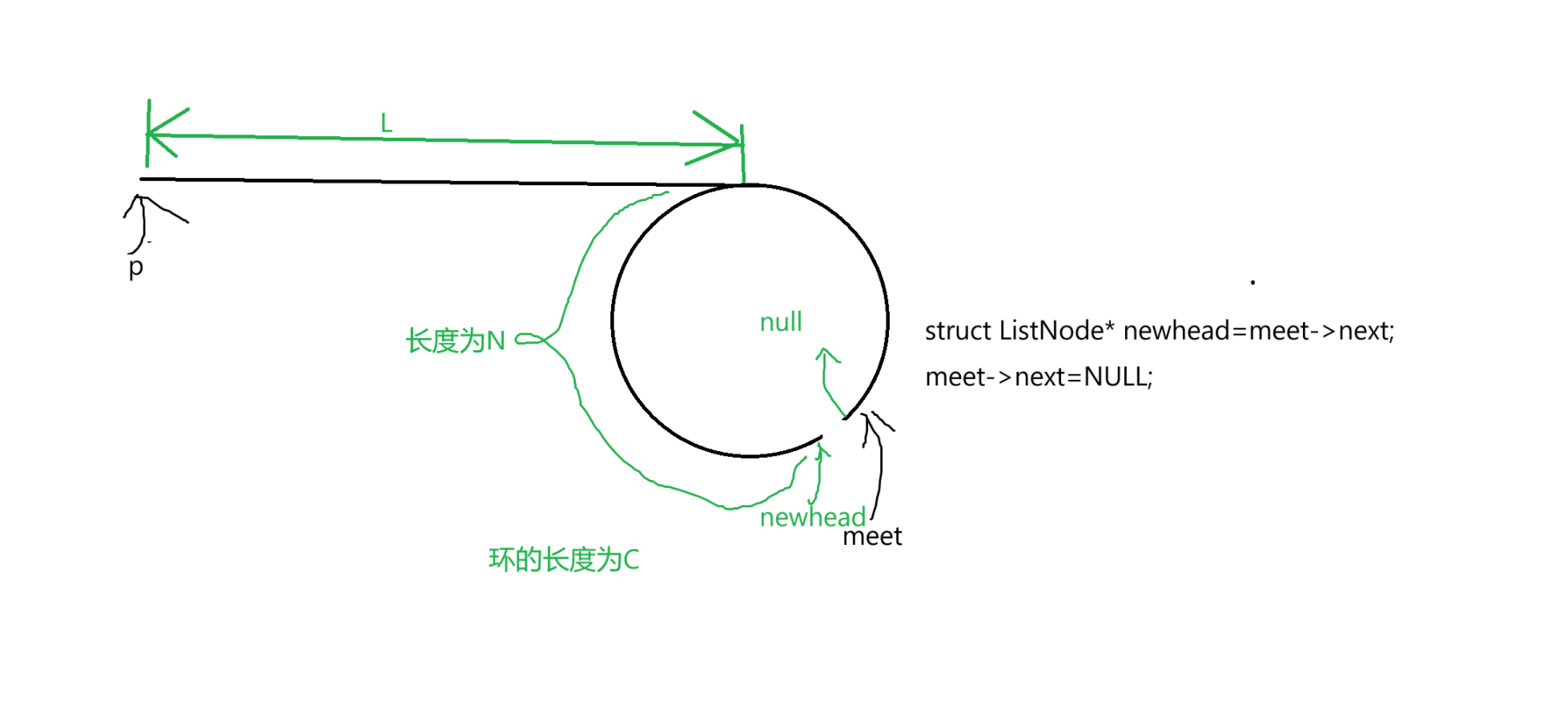
如图所示,此时我们让把meet的下一个节点记为newhead,让meet的下一个指向空。
此时以p为头的链表的结尾是meet,以newhead为头的链表结尾也是meet,两个链表相交。
只需要返回两个链表的相交节点即可。如果题目说了不能修改链表,那就最后再修复即可。
对于返回相交链表的相交节点,也是有原题的:Leetcode 160
在这里就不进行代码演示了,感兴趣的读者可以前去尝试一下。
随机链表的复制
在这里介绍一下什么是随机链表:
就是在正常的链表节点处加入了一个随机指针random,这个指针可能指向链表当中的任意一个元素。
定义如下:
struct Node {
int val;
struct Node *next;
struct Node *random;
};
原题:Leetcode 138
先来分析一下,如果单纯只是复制链表,那很简单。但是对于random指针的赋值是比较难的,因为题目说了新的链表的random指针并不是指向原来链表的那些节点。而是要根据原来链表random指针指向相对于整个链表的位置来拷贝。
说人话就是,复制一个一模一样的链表出来。
鉴于单向链表(不含random指针)的复制是很容易的,在这里提出第一种思路:
先复制出一个单向链表,random区域的指针先指向原来对应节点的 random区域。然后声名一个变量offset,遍历原来链表种所有的random区,并且判断这个random区域在链表的第几个节点,然后在新链表中根据这个偏移量offset去赋值新链表的random区域,代码如下:
struct Node* NewListNode(int val,struct Node* random){
struct Node* new=(struct Node*)malloc(sizeof(struct Node));
new->val=val;
new->random=random;
new->next=NULL;
return new;
}
void NodeListPushback(struct Node** CpyHead,int VAL,struct Node* RANDOM){
//使用二级指针作为参数是因为,我们传参的时候传的是cpyHead,是一个一级指针
//尾插是需要改变指针的指向,即地址值,所以要传址调用
if(*CpyHead==NULL){
*CpyHead=NewListNode(VAL,RANDOM);
return;
}
//找尾插入
struct Node* p=*CpyHead;
while(p->next){
p=p->next;
}
p->next=NewListNode(VAL,RANDOM);
return;
}
struct Node* copyRandomList(struct Node* head) {
if(head==NULL) return NULL;
struct Node* pmove = head;
struct Node* cpyHead = NULL;
// pmove操作原链表,cpyHead是复制链表的头
// 先复制链表(且先让新链表的random区指向旧的链表的对应random区)
while (pmove) {
NodeListPushback(&cpyHead, pmove->val, pmove->random); // 传址调用
pmove = pmove->next;
}
// 修改random区域
pmove = head;
struct Node* pcpy = cpyHead;
while (pmove) {
if (pmove->random == NULL) pcpy->random = NULL;
pmove = pmove->next;
pcpy = pcpy->next;
} // 先把random区域为NULL的搞定
pmove = head;
int Offset = 0; // random区相较于开头的相对位置
while (pmove) {
struct Node* random_cpy = cpyHead;
int count = Offset;
while (count--) random_cpy = random_cpy->next;
pcpy = cpyHead;
while (pcpy) {
if (pcpy->random == pmove) pcpy->random = random_cpy;
pcpy = pcpy->next;
}
Offset++;
pmove=pmove->next;
}
return cpyHead;
}
其中, NewListNode函数是开辟新节点,NodeListPushback函数是尾插。通过这两个函数就成功完成了上述的第一步。
然后后续就是根据偏移量Offset来判断原链表的每个random区在链表中的相对位置,然后新链表中的所有指向这个random区域的都要指向这个相对位置的节点处。
但是这个思路有一个的缺点就是:代码冗长,时间复杂度过高O为(N^2)。
有没有一种办法能够让时间复杂度降为O(N)呢?
我们这样操作:
我们得想办法让新的链表与旧的链表产生一些联系。假设能做到这样一种情况就最好:
用一个指针cpy指向拷贝的链表,origin指针指向cpy指向节点对应在原来链表的节点。然后通过origin指针找到random区域的过程中找到cpy该指向的位置。
我们试着这样子把两个链表先连起来,然后我们来分析一下可不可行。
上面蓝色部分的线是next指针区域的。
如果origin的random是NULL,就直接让cpy的random为NULL。
如果不是,假设origin的random随便指向原链表的任意一个非空结点:
我们发现,origin->random指向值,正好与origin->random->next的值一样。
然后只要origin不为空,就重复上述操作即可。这样子,也就是在连接链表的时候遍历了一次链表,然后在赋值random区域的时候遍历一次链表,最后恢复链表再遍历一次。因为没有循环的嵌套,所以时间复杂度为O(N)。
代码实现:
void PushBack_Same_Val(struct Node** head){
struct Node* new=(struct Node*)malloc(sizeof(struct Node));
new->random=NULL;
new->val=(*head)->val;
new->next=(*head)->next;
(*head)->next=new;
}
struct Node* copyRandomList(struct Node* head) {
if(head==NULL) return NULL;
struct Node* Push_Head=head;
while(Push_Head){
PushBack_Same_Val(&Push_Head);
Push_Head=Push_Head->next->next;
}
//到这一步 新的链表与旧的链表已经进行了结合了 建立了一些关系 时间复杂度O(N)
struct Node* origin=head,*cpy=head->next;
//分别操作原来链表和被复制的链表
while(origin){
if(origin->random!=NULL) cpy->random=origin->random->next;
origin=cpy->next;
if(origin!=NULL) cpy=origin->next;
}
//random区操作完毕
//链接两个链表 只对next操作
origin=head;
cpy=head->next;
struct Node* preturn=cpy;
while(origin!=NULL){
origin->next=cpy->next;
origin=origin->next;
if(origin) cpy->next=origin->next;
else cpy->next=NULL;
cpy=cpy->next;
}
return preturn;
}