目录
一、前言
最短路问题一般我们都是在图论中会遇到的问题,对应的算法有 Dijkstra 算法,Bellman-Ford 算法,Floyd-Warshall 算法。上面的三个算法后续在图论的文章里面会单独再介绍(内容比较多),今天主要介绍使用 BFS 来解决边权为 1 的最短路问题,边权为 1 的这个条件可以衍生为边权全部相同。为了方便叙述下面所有的最短路问题都是边权全部相同的情况。
1.1 如何使用 BFS 找到最短路:
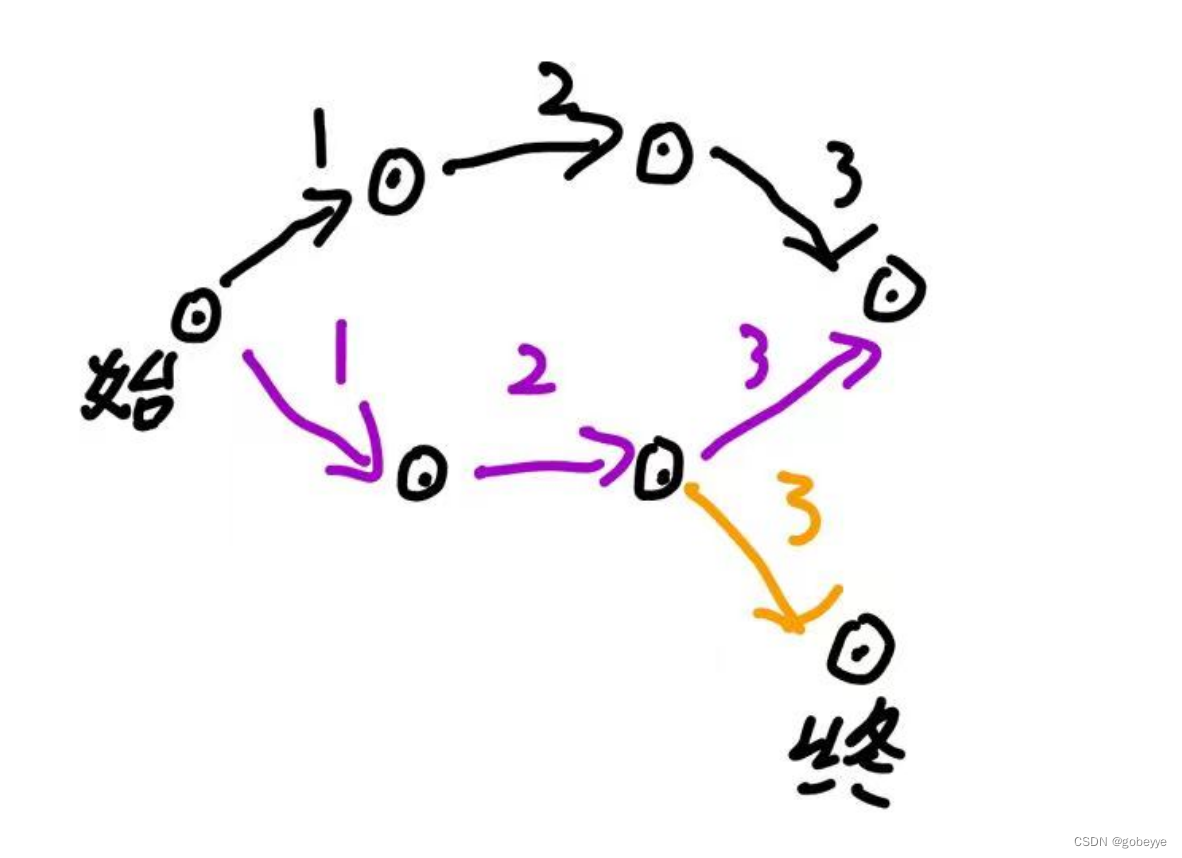
解法:从起点开始,来一次 BFS 即可。扩展的层数就是最短路的长度,一旦遍历到终点立即返回对应的层数,就是最短路的长度。对应过程如下图 BFS 就是对应每条路径(不同颜色)同时在周围扩散一步。
1.2 为什么不用 dfs :
使用 dfs 大概率会超时,因为:bfs 不用遍历所有节点,找到直接返回就是最小值。而 dfs 必须要把全部路径都找一遍才能找到最小值,时间复杂度是比较高的,所以这类问题我们一般使用 bfs 来解决。
二、模板套路
• 参数解释:
map:对应查找数组。
sr | sc:起点坐标。
er | ec:终点坐标。
path:记录路径长度。
vis:去重。
public int bfs(char[][] map,int sr,int sc,int er,int ec){
Queue<int[]> queue = new LinkedList<>();
queue.offer(new int[]{sr,sc});//先放入起点
int path = 0;//记录路径长度
while(!queue.isEmpty()){
int size = queue.size();
path++;//向外扩展一层
for(int i = 0;i < size;i++){
int[] tmp = queue.poll();
int a = tmp[0],b = tmp[1];
vis[a][b] = true;
for(int k = 0;k < 4;k++){
int x = a + dx[k];
int y = b + dy[k];
if(x >= 0 && x < n && y >= 0 && y < m && 题目对应条件 &&
!vis[x][y]){
if(达到出口条件){
return path;//返回
}
queue.offer(new int[]{x,y});
vis[x][y] = true;
}
}
}
}
return -1;//没找到的情况,具体返回什么看题目
}上面就是大体的框架,默认起点不会是终点(题目要求可以的话,来个特判即可),如果对 BFS 不是很熟悉的话可以结合 BFS解决FloodFIll算法 来学习。
三、例题练习
3.1 例题1:迷宫中离入口最近的出口
• 题目链接:迷宫中离入口最近的出口
• 问题描述:
给你一个 m x n 的迷宫矩阵 maze (下标从 0 开始),矩阵中有空格子(用 '.' 表示)和墙(用 '+' 表示)。同时给你迷宫的入口 entrance ,用 entrance = [entrancerow, entrancecol] 表示你一开始所在格子的行和列。
每一步操作,你可以往 上,下,左 或者 右 移动一个格子。你不能进入墙所在的格子,你也不能离开迷宫。你的目标是找到离 entrance 最近 的出口。出口 的含义是 maze 边界 上的 空格子。entrance 格子 不算 出口。
请你返回从 entrance 到最近出口的最短路径的 步数 ,如果不存在这样的路径,请你返回 -1 。
• 解题思路:
利用 BFS 来解决是这类题目最经典(边权为 1 的最短路问题)的做法。从起点开始 BFS ,用 path 来记录当前遍历的层数,这样就能在找到出口的时候,返回起点到出口的最短长度。基本就是套模板即可,不同的是终点是在边界地方而不是作为 bfs 参数。
• 代码编写:
class Solution {
int n,m;
boolean[][] vis;
int[] dx = {0,0,1,-1};
int[] dy = {1,-1,0,0};
public int nearestExit(char[][] maze, int[] entrance) {
n = maze.length;
m = maze[0].length;
vis = new boolean[n][m];
int ans = bfs(maze,entrance[0],entrance[1]);
return ans;
}
public int bfs(char[][] map,int sr,int sc){
Queue<int[]> queue = new LinkedList<>();
queue.offer(new int[]{sr,sc});
int path = 0;
while(!queue.isEmpty()){
int size = queue.size();
path++;//向外扩展一层
for(int t = 0;t < size;t++){
int[] tmp = queue.poll();
int a = tmp[0],b = tmp[1];
vis[a][b] = true;
for(int k = 0;k < 4;k++){
int x = a + dx[k];
int y = b + dy[k];
if(x >= 0 && x < n && y >= 0 && y < m && map[x][y] == '.' &&
!vis[x][y]){
if(x == 0 || x == n - 1 || y == 0 || y == m - 1){
return path;
}
queue.offer(new int[]{x,y});
vis[x][y] = true;
}
}
}
}
return -1;
}
}3.2 例题2:最小基因变化
• 题目链接:最小基因变化
• 问题描述:
基因序列可以表示为一条由 8 个字符组成的字符串,其中每个字符都是 'A'、'C'、'G' 和 'T' 之一。
假设我们需要调查从基因序列 start 变为 end 所发生的基因变化。一次基因变化就意味着这个基因序列中的一个字符发生了变化。
- 例如,
"AACCGGTT" --> "AACCGGTA"就是一次基因变化。
另有一个基因库 bank 记录了所有有效的基因变化,只有基因库中的基因才是有效的基因序列。(变化后的基因必须位于基因库 bank 中)
给你两个基因序列 start 和 end ,以及一个基因库 bank ,请你找出并返回能够使 start 变化为 end 所需的最少变化次数。如果无法完成此基因变化,返回 -1 。
注意:起始基因序列 start 默认是有效的,但是它并不一定会出现在基因库中。
• 解题思路:
首先因为字符变化并没有权重,所以这是边权为 1 的最短路问题。那么如何枚举出所有的变化情况呢?答:暴力,因为题目的数据都很小,我们可以把字符串每个位置的字符都用 'A','C','G','T'来替换看看在不在基因库中存在,如果存在且没有被找过,存入到队列中。我们可以使用语言带的哈希表来标记搜索过的地方。
优化:我们预先处理基因库,把基因库里面的数据存入到哈希表中,这样就可以用O(1)的时间复杂度来快速找到。
• 代码编写:
class Solution {
public int minMutation(String startGene, String endGene, String[] bank) {
// BFS
// 1.创建 哈希表 来快速判断
Set<String> hash = new HashSet<>();// 用来快速判断一个字符串是否再bank里面出现
Set<String> vis = new HashSet<>();// 用来标记已经变化过的字符串
char[] change = { 'A', 'C', 'G', 'T' };
for (String tmp : bank) {
hash.add(tmp);
}
if (startGene.equals(endGene)) {// 处理边界情况
return 0;
}
if (!hash.contains(endGene)) {
return -1;
}
Queue<String> queue = new LinkedList<>();
queue.offer(startGene);//存入开始位置
int path = 0;
while (!queue.isEmpty()) {
path++;// 代表剥离一层
int size = queue.size();
for (int i = 0; i < size; i++) {// 找出全部变化
String tmp = queue.poll();
vis.add(tmp);
for (int j = 0; j < 8; j++) {// 把8个位置上的元素全部修改
char[] s = tmp.toCharArray();//细节问题,不能放在外面,因为放在
//外面那么就不能保证只修改一个元素了
for (int k = 0; k < 4; k++) {
s[j] = change[k];
String next = new String(s);//char[]是不能toString的
if (next.equals(endGene)) {//找到出口
return path;
}
if (hash.contains(next) && !vis.contains(next)) {
queue.offer(next);
vis.add(next);
}
}
}
}
}
return -1;
}
}3.3 例题3:单词接龙
• 题目链接:单词接龙
• 问题描述:
字典 wordList 中从单词 beginWord 和 endWord 的 转换序列 是一个按下述规格形成的序列 beginWord -> s1 -> s2 -> ... -> sk:
- 每一对相邻的单词只差一个字母。
- 对于
1 <= i <= k时,每个si都在wordList中。注意,beginWord不需要在wordList中。 sk == endWord
给你两个单词 beginWord 和 endWord 和一个字典 wordList ,返回 从 beginWord 到 endWord 的 最短转换序列 中的 单词数目 。如果不存在这样的转换序列,返回 0 。
• 解题思路:
这题可以说是例题2的升级版,因此基本解法是一样的,区别就是例题2是 4 个字符替换,本题是26个字符替换。注意这题找不到是返回 0。
优化:如果 endWord 不在 wordList 中直接返回 0 即可。
• 代码编写:
class Solution {
public int ladderLength(String beginWord, String endWord, List<String> wordList) {
//最短路径问题,权值是相同的
//采用 BFS 来解决
char[] change = new char[26];
for(int i = 0;i < 26;i++){
change[i] = (char)(i + 'a');
}
Set<String> hash = new HashSet<>();//用来记录字典
Set<String> set = new HashSet<>();//用来去重
//处理一些边界情况
//题目说明了不会出现这种情况
for(String s:wordList){
hash.add(s);
}
if(!hash.contains(endWord)){//不存在的情况
return 0;
}
Queue<String> queue = new LinkedList<>();
queue.offer(beginWord);
int n = beginWord.length();//每个单词有多长
//进行 BFS 查找
int path = 1;//用来记录层数
while(!queue.isEmpty()){
int size = queue.size();
path++;
for(int i = 0;i < size;i++){
String next = queue.poll();
set.add(next);
for(int j = 0;j < n;j++){
char[] s = next.toCharArray();//方便替换
for(int k = 0;k < 26;k++){
s[j] = change[k];
String tmp = new String(s);
if(tmp.equals(endWord)){//找到答案
return path;
}
if(hash.contains(tmp) && !set.contains(tmp)){
queue.offer(tmp);
set.add(tmp);//标记为找到了
}
}
}
}
}
return 0;//注意这题找不到是返回0
}
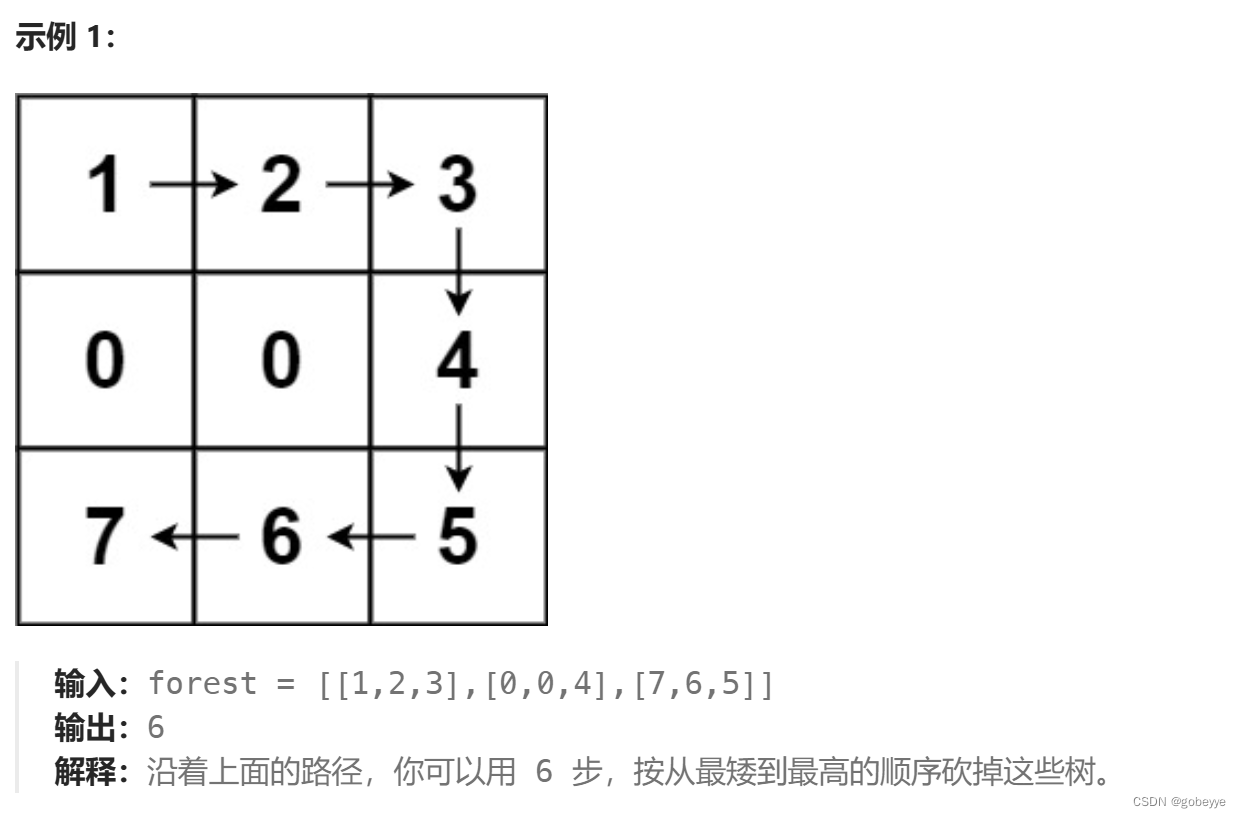
}3.4 例题4:为高尔夫比赛砍树
• 题目链接:为高尔夫比赛砍树
• 问题描述:
你被请来给一个要举办高尔夫比赛的树林砍树。树林由一个 m x n 的矩阵表示, 在这个矩阵中:
0表示障碍,无法触碰1表示地面,可以行走比 1 大的数表示有树的单元格,可以行走,数值表示树的高度
每一步,你都可以向上、下、左、右四个方向之一移动一个单位,如果你站的地方有一棵树,那么你可以决定是否要砍倒它。
你需要按照树的高度从低向高砍掉所有的树,每砍过一颗树,该单元格的值变为 1(即变为地面)。
你将从 (0, 0) 点开始工作,返回你砍完所有树需要走的最小步数。 如果你无法砍完所有的树,返回 -1 。
可以保证的是,没有两棵树的高度是相同的,并且你至少需要砍倒一棵树。
• 解题思路:
1. 找出砍树的顺序。
2. 按照砍树的顺序,一个一个的用 bfs 求出最短路即可(封装成一个函数)。
• 代码编写:
直接利用语言自带 sort 排序,注意每次传入 bfs 求最短路的起点和终点每次都不一样,要一直更新。
class Solution {
int n,m;
public int cutOffTree(List<List<Integer>> forest) {
n = forest.size();
m = forest.get(0).size();
//1.把不为0的数的下标存入list
List<int[]> ret = new ArrayList<>();
for(int i = 0;i < n;i++){
for(int j = 0;j < m;j++){
if(forest.get(i).get(j) > 1){
ret.add(new int[]{i,j});
}
}
}
//2.排序
Collections.sort(ret,(o1,o2) -> {
return forest.get(o1[0]).get(o1[1]) > forest.get(o2[0]).get(o2[1]) ? 1 : -1;
});//从小到大排序
//3.从小到大用dfs找,找不到返回-1
int path = 0;
int sum = 0;//最后全部的和
int x = 0,y = 0;//起点
for(int[] tmp:ret){
path = bfs(forest,x,y,tmp[0],tmp[1]);
if(path == -1){
return -1;//找不到立即返回 -1
}
x = tmp[0];y = tmp[1];//每个起点是不一样的,要一直更新
sum += path;
}
return sum;
}
int[] dx = {0,0,1,-1};
int[] dy = {1,-1,0,0};
public int bfs(List<List<Integer>> f, int bx, int by, int ex, int ey)
{
if(bx == ex && by == ey) return 0;//可能起点即终点
Queue<int[]> q = new LinkedList<>();
boolean[][] vis = new boolean[n][m];
q.add(new int[]{bx, by});
vis[bx][by] = true;
int step = 0;
while(!q.isEmpty())
{
int sz = q.size();
step++;
while(sz-- != 0)
{
int[] t = q.poll();
int a = t[0], b = t[1];
for(int i = 0; i < 4; i++)
{
int x = a + dx[i], y = b + dy[i];
if(x >= 0 && x < n && y >= 0 && y < m && f.get(x).get(y)
!= 0 && !vis[x][y])
{
if(x == ex && y == ey) return step;
q.add(new int[]{x, y});
vis[x][y] = true;
}
}
}
}
return -1;
}
}结语:
其实写博客不仅仅是为了教大家,同时这也有利于我巩固知识点,和做一个学习的总结,由于作者水平有限,对文章有任何问题还请指出,非常感谢。如果大家有所收获的话还请不要吝啬你们的点赞收藏和关注,这可以激励我写出更加优秀的文章。