开放地址法:【C++进阶学习】第九弹——哈希的原理与实现——开放寻址法的讲解-CSDN博客
前言:
哈希的整体思想就是建立映射关系,前面的开放地址法的讲解中,也对哈希的原理做了详细的讲解,今天就来讲解一下实现哈希的另一种主要方法——链地址法
目录
一、链地址法的基本思想
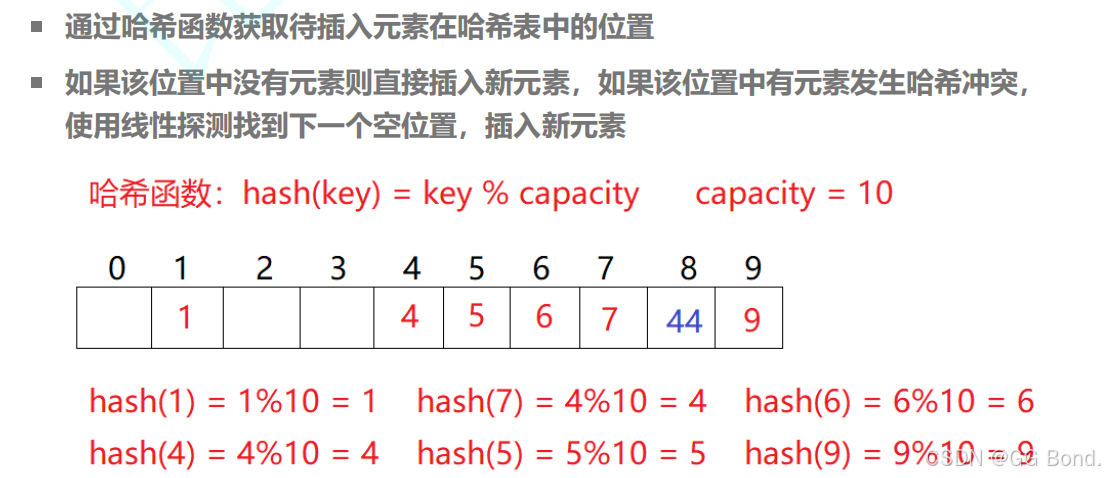
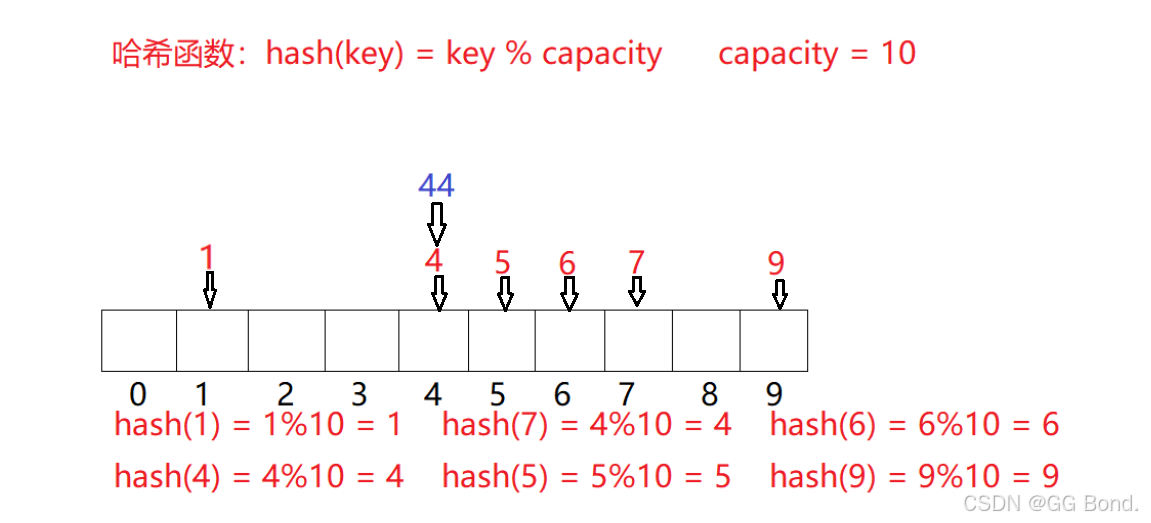
前面所讲的开放地址法,我们是通过建立一种映射的关系来存储数据
这种方法时常会遇到图中的这种情况,有利有弊
链地址法则是另一种思路:将哈希表的每个槽指向一个链表(或其他数据结构,如动态数组,红黑树等),所有哈希到同一个槽的元素都存储在这个链表中。这样,即使发生了哈希冲突,也可以通过链表来存储多个元素。
二、链地址法的实现步骤
首先,我们先来看一下链地址法的重点:
- 定义哈希表结构:哈希表通常包含一个数组,数组的每个元素是一个链表的头节点。
- 哈希函数:设计一个哈希函数,将键映射到数组的索引位置。
- 插入操作:
- 计算键的哈希值,得到索引位置。
- 将键值对插入到对应索引位置的链表中。
- 查找操作:
- 计算键的哈希值,得到索引位置。
- 在对应索引位置的链表中查找键值对。
- 删除操作:
- 计算键的哈希值,得到索引位置。
- 在对应索引位置的链表中删除键值对。
节点结构
与开放寻址法一样,因为我们并不知道插入要操作何种类型的数据,可能是整形,浮点型或string的,所以我们可以选择将它们全转化为整形来处理,这里就需要我们借助仿函数和模板特化来实现
template<class K>
struct HashFunc //仿函数,这里的功能是将其他类型转化为整形
{
size_t operator()(const K& key)
{
return (size_t)key;
}
};
template<> //特化
struct HashFunc<string> //string类的不可以直接转化为整形,所以需要特殊处理
{
size_t operator()(const string& key)
{
size_t hash = 0;
for (auto e : key)
{
hash *= 31;
hash += e;
}
return hash;
}
};
template<class K,class V>
struct HashNode
{
HashNode* next;
pair<K, V> _kv;
HashNode(const pair<K,V>& kv) //构造函数
:next(nullptr) //初始化列表
,_kv(kv)
{}
};
template<class K,class V, class Hash = HashFunc<K>>
class HashTable
{
typedef HashNode<K, V> Node;
public:
private:
//vector<list> _tables; //这也是一种思路
vector<Node*> _tables;
size_t _n;
};
构造和析构
因为在节点中我们使用了指针类型的数据,所以我们尽量将构造和析构函数自己定义,这里没啥难度,看代码即可:
HashTable()
{
_tables.resize(10); //初始化大小为19
}
~HashTable()
{
for (int i = 0; i < _tables.size(); i++)
{
Node* cur = _tables[i]; //每个链表的头节点
while (cur) //遍历链表,清空链表中的所有元素
{
Node* next = cur->next;
delete cur;
cur = next;
}
_tables[i] = nullptr;
}
}插入操作
链地址法插入操作的基本思路就是:
1、选择合适的哈希函数,确定数组大小
2、通过哈希函数找到自己所对应的位置,并进行头插
3、当负载因子过大时进行扩容
bool Insert(const pair<K, V>& kv)
{
Hash hf;
if (Find(kv.first))
return false;
//负载因子最大到1,到1时进行扩容
//我们提供这样一个思路:如果数据真的非常多的时候,用链表来存储,因为要
// 考虑负载因子的原因,其实是比较浪费空间的,我们
// 可以把节点结构进行更改,改成红黑树的结构
if (_n == _tables.size())
{
扩容
//size_t newSize = _tables.size() * 2;
//HashTable<K, V> newHT;
//newHT._tables.resize(newSize);
遍历旧表
//for (size_t i = 0; i < _tables.size(); i++)
//{
// Node* cur = _tables[i];
// while (cur)
// {
// newHT.Insert(cur->_kv);
// cur = cur->next;
// }
//}
//_tables.swap(newHT._tables);
//方法二
vector<Node*> newTables;
newTables.resize(_tables.size() * 2);
for (size_t i = 0; i < _tables.size(); i++)
{
Node* cur = _tables[i];
while (cur)
{
Node* next = cur->next;
size_t hashi = hf(cur->_kv.first) % newTables.size();
cur->next = newTables[hashi];
newTables[hashi] = cur;
cur = next;
}
_tables[i] = nullptr;
}
_tables.swap(newTables);
}
size_t hashi = hf(kv.first) % _tables.size(); //哈希函数
Node* newnode = new Node(kv);
//头插
newnode->next = _tables[hashi];
_tables[hashi] = newnode;
++_n;
return true;
}
查找操作
上面的插入操作中,我们首先就先用查找操作看是否已经有这个数据,因为哈希是不允许存在重复数据的,这里我们就来看一下这个查找操作,首先是先通过哈希函数找到对应的头节点,然后在对应的链表中进行查找
Node* Find(const K& key)
{
Hash hf;
size_t hashi = hf(key) % _tables.size();
Node* cur = _tables[hashi];
while (cur)
{
if (cur->_kv.first == key)
return cur;
cur = cur->next;
}
return nullptr;
}
删除操作
删除操作也是先通过哈希函数找到删除元素的头节点,然后就是链表中元素的删除那一套操作
bool Erase(const K& key)
{
Hash hf;
size_t hashi = hf(key) % _tables.size();
Node* cur = _tables[hashi];
Node* parent = nullptr;
while (cur)
{
if (cur->_kv.first == key)
{
if (parent == nullptr)
{
_tables[hashi] = cur->next;
}
else
{
parent->next = cur->next;
}
delete cur;
cur = nullptr;
return true;
}
parent = cur;
cur = cur->next;
}
return false;
}
打印操作
链地址法我们一般需要观测的数据是链表个数,链表长度等(链表在这里也成为桶,即哈希桶),所以我们这里打印的是与链表个数、长度等相关的
void Some()
{
size_t bucketSize = 0; //桶的个数
size_t maxbucketLen = 0; //最大桶长
size_t sum=0; //总的元素个数
double averagebucketLen = 0; //平均桶长
for (size_t i = 0; i < _tables.size(); i++)
{
Node* cur = _tables[i];
if (cur)
{
++bucketSize;
}
size_t bucketLen = 0;
while (cur)
{
++bucketLen;
cur = cur->next;
}
sum += bucketLen;
if (bucketLen > maxbucketLen)
{
maxbucketLen = bucketLen;
}
}
averagebucketLen = (double)sum / (double)bucketSize;
cout << "桶的个数:" << bucketSize << endl;
cout << "桶的最大长度:" << maxbucketLen << endl;
cout << "平均桶的长度:" << averagebucketLen << endl;
}
三、测试代码
我们给出几个测试用例检验一下上面的方法是否有误:
测试一:
void TestHT1() //测试插入,查找和删除操作是否有误
{
HashTable<int, int> ht;
int a[] = { 4,14,24,34,5,7,1 };
for (auto e : a)
{
ht.Insert(make_pair(e, e));
}
cout << ht.Find(4) << endl; //如果成功插入,这里会返回一个地址
ht.Erase(4); //删除节点
cout << ht.Find(4) << endl; //删除后会返回nullptr
}
运行结果:
测试二:
void TestHT2() //测试string
{
string arr[] = { "香蕉","甜瓜","苹果","香蕉","苹果","苹果" };
HashTable<string, int> ht;
for (auto e : arr)
{
auto ret = ht.Find(e);
if (ret)
ret->_kv.second++;
else
{
ht.Insert(make_pair(e, 1));
}
}
ht.Some(); //通过桶的相关信息可以推断出插入情况
}
运行结果:
四、总结
以上就是链地址法的内容,链地址法与开放地址法各有千秋,总的来说开放地址法时间复杂度更低,都是当数据过多时需要的空间多,链地址法节省空间但是效率上稍微偏低,在应用时要结合实际情况进行取舍
感谢各位大佬观看,创作不易,还请各位大佬点赞支持!!!