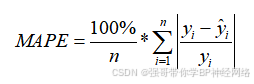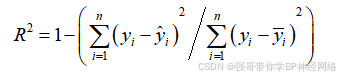一、回归模型评估指标
在模型评估中,常用的指标包括MAE(平均绝对误差)、RMSE(均方根误差)、MAPE(平均绝对百分比误差)、MSE(均方误差)和R²(决定系数)等。这些指标各有特点和适用范围,下面将逐一进行介绍。
1.MAE(Mean Absolute Error,平均绝对误差)
MAE是评估预测模型精度的一种常用指标,它计算的是每个样本的预测误差的绝对值的平均数。MAE的优点在于它能直观地表示模型预测值与真实值之间的差距大小,且对所有误差的大小都给予相同重视,对异常值的敏感性相对稳定。MAE的取值范围是[0,+∞),当预测值与真实值完全吻合时等于0,即完美模型;误差越大,该值越大。
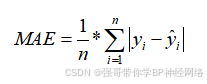
2.RMSE(Root Mean Squared Error,均方根误差)
RMSE是预测值与真实值偏差的平方与观测次数n比值的平方根,它衡量的是预测值与真实值之间的偏差程度。RMSE的优点在于其对数据中的异常值较为敏感,能够反映出模型预测的精度。在实际应用中,RMSE常用于评估回归模型的预测精度。根据经验法则,RMSE值在0.2~0.5之间通常认为模型能够较准确地预测数据。RMSE的取值范围是0到正无穷大,数值越小表示模型的预测误差越小,模型的预测能力越强。
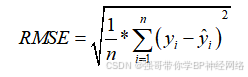
3.MAPE(Mean Absolute Percentage Error,平均绝对百分比误差)
MAPE是评价预测值和实际值之间误差的度量方式,它以百分比形式出现,表示在预测值与实际值之间相对误差的平均百分比。MAPE的优点在于以百分比形式表示预测值与真实值之间的相对误差,更关注相对误差,对于不同量级的预测问题更具可比性。在金融领域中,MAPE常用于评估投资组合风险模型的表现。一般来说,MAPE小于10%被认为是比较好的预测模型,MAPE在10%~20%之间,预测的精度还可以接受;但如果MAPE大于20%,则预测效果不太理想。然而,MAPE的缺点在于当真实值接近零时,计算会出现分母为零的情况,导致评价结果不可用。
4.MSE(Mean Squared Error,均方误差)
MSE是评估预测模型精度的另一种常用指标,它计算的是每个样本的预测误差的平方的平均数。MSE的优点在于它能够将不同单位的误差转化为同一单位进行比较,且对异常值较为敏感。然而,MSE的缺点在于它放大了较大误差的影响,可能导致评估结果不够稳定。MSE的取值范围是0到正无穷大,数值越小表示模型的预测误差越小。
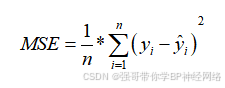
5.R²(R-squared,决定系数)
R²是评估回归模型对观测数据拟合程度的一种指标,其取值范围在0到1之间。R²越接近1,表示模型拟合得越好;越接近0,则表示拟合效果较差。R²的计算公式是R²=(TSS – RSS)/TSS,其中TSS为总离差平方和(实际值和实际值均值之间的差值平方和),RSS为残差平方和(实际值和预测值之间的差值平方和)。R²反映的是因变量y的变异中有多少百分比可由自变量x的变异来解释,即表征依变数Y的变异中有多少百分比可由控制的自变数X来解释。
综上所述,不同的模型评估指标各有优缺点和适用范围,在选择时应根据具体问题和需求进行权衡。
二、超参数调优
超参数调优是机器学习中的一项重要任务,它涉及调整模型参数以改善模型在未见数据上的表现。交叉验证、网格搜索和随机搜索是几种常用的超参数调优方法。下面我将分别介绍这三种方法及其如何应用于超参数调优。
1.交叉验证(Cross-Validation)
交叉验证是一种评估统计模型性能的方法,它将数据集分成几个较小的子集,称为“折”(folds)。这些子集被用作训练集和测试集,通过轮换不同的子集作为测试集来评估模型的性能。
步骤:
(1)划分数据集:将数据集分成K个大小相似的互斥子集。
(2)循环训练测试:对于每个子集,轮流将其作为测试集,其余K-1个子集作为训练集,训练模型并评估其在测试集上的性能。
(3)计算性能:汇总所有测试集上的性能指标(如准确率、召回率等),并计算其平均值作为模型性能的最终估计。
代码如下:
from sklearn.model_selection import cross_val_score # 使用交叉验证评估模型性能
cv_scores = cross_val_score(model, X_train, y_train, cv=5) # 输出交叉验证得分
print("交叉验证得分:", cv_scores)
print("平均交叉验证得分:", np.mean(cv_scores))
2.网格搜索(Grid Search)
网格搜索是一种穷举搜索方法,它通过遍历指定的参数值网格来确定最佳参数组合。通过对参数进行全面搜索可能的参数组合,唯一的缺点的是计算量大,尤其是当参数空间和每个参数的可能值很多时。
步骤:
(1)定义参数网格:为每个待调优的超参数定义一个值的列表,形成一个网格。
(2)遍历网格:对于网格中的每一组参数值,使用这些参数值训练模型,并评估其性能。
(3)选择最佳参数:选择表现最好的参数组合作为最佳参数。
代码如下:
from sklearn.model_selection import GridSearchCV
from sklearn.svm import SVR
from sklearn import datasets
dataset = datasets.load_iris()
X = dataset.data
y = dataset.target
grid = GridSearchCV(
estimator=SVR(kernel='rbf'),
param_grid={
'C': [0.1, 1, 10, 100],
'epsilon': [0.0001, 0.001, 0.01, 0.1, 1, 10],
'gamma': [0.001, 0.01, 0.1, 1]
},
cv=5, scoring='neg_mean_squared_error', verbose=0, n_jobs=-1)
grid.fit(X, y)
print(grid.best_score_)
print(grid.best_params_)
3.随机搜索(Random Search)
随机搜索通过随机选择参数值来优化超参数,而不是像网格搜索那样系统地遍历所有可能的值。比网格搜索更高效,尤其是在参数空间很大且许多参数对模型性能影响较小时。果可能不是全局最优的,但通常足够好。
步骤:
(1)定义参数分布:为每个待调优的超参数定义一个值的分布(如均匀分布、正态分布等)。
(2)随机抽样:从每个参数的分布中随机抽取一定数量的样本作为参数组合。
(3)训练评估:对每个参数组合训练模型并评估其性能。
(4)选择最佳参数:从随机抽样的参数组合中选择表现最好的作为最佳参数。
代码如下:
from scipy.stats import randint as sp_randint
from sklearn.model_selection import RandomizedSearchCV
rom sklearn.datasets import load_digits
from sklearn.ensemble import RandomForestClassifier
# 载入数据
digits = load_digits()
X, y = digits.data, digits.target
# 建立一个分类器或者回归器
clf = RandomForestClassifier(n_estimators=20)
# 给定参数搜索范围:list or distribution
param_dist = {"max_depth": [3, None], # 给定list
"max_features": sp_randint(1, 11), # 给定distribution
"min_samples_split": sp_randint(2, 11), # 给定distribution
"bootstrap": [True, False], # 给定list
"criterion": ["gini", "entropy"]} # 给定list
# 用RandomSearch+CV选取超参数
n_iter_search = 20
random_search = RandomizedSearchCV(clf, param_distributions=param_dist, n_iter=n_iter_search, cv=5, iid=False)
grid.fit(X, y)
print(grid.best_score_)
print(grid.best_params_)
三、实践调优BP神经网络的超参数,如学习率、隐藏层大小等
import torch
import torch.nn as nn
import torch.optim as optim
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
# 生成模拟数据
X, y = make_classification(n_samples=1000, n_features=20, n_informative=2, n_redundant=10, random_state=42)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 转换为PyTorch张量
X_train_tensor = torch.tensor(X_train, dtype=torch.float32)
y_train_tensor = torch.tensor(y_train, dtype=torch.long)
X_test_tensor = torch.tensor(X_test, dtype=torch.float32)
y_test_tensor = torch.tensor(y_test, dtype=torch.long)
# 定义神经网络模型
class NeuralNetwork(nn.Module):
def __init__(self, input_size, hidden_size, num_classes):
super(NeuralNetwork, self).__init__()
self.fc1 = nn.Linear(input_size, hidden_size)
self.relu = nn.ReLU()
self.fc2 = nn.Linear(hidden_size, num_classes)
def forward(self, x):
out = self.fc1(x)
out = self.relu(out)
out = self.fc2(out)
return out
# 超参数搜索空间
hidden_sizes = [10, 50, 100] # 隐藏层大小选项
learning_rates = [0.01, 0.001, 0.0001] # 学习率选项
best_accuracy = 0.0
best_hyperparams = None
# 遍历所有超参数组合
for hidden_size in hidden_sizes:
for learning_rate in learning_rates:
model = NeuralNetwork(input_size=X_train.shape[1], hidden_size=hidden_size, num_classes=2)
criterion = nn.CrossEntropyLoss()
optimizer = optim.SGD(model.parameters(), lr=learning_rate)
# 训练模型
for epoch in range(100): # 假设我们训练100个epoch
optimizer.zero_grad()
outputs = model(X_train_tensor)
loss = criterion(outputs, y_train_tensor)
loss.backward()
optimizer.step()
# 评估模型
with torch.no_grad():
predictions = model(X_test_tensor)
_, predicted = torch.max(predictions.data, 1)
accuracy = accuracy_score(y_test, predicted.numpy())
print(f"Accuracy: {accuracy} with hidden_size={hidden_size} and learning_rate={learning_rate}")
if accuracy > best_accuracy:
best_accuracy = accuracy
best_hyperparams = {'hidden_size': hidden_size, 'learning_rate': learning_rate}
print(
f"New best accuracy: {best_accuracy} with hidden_size={hidden_size} and learning_rate={learning_rate}")
print(f"Best hyperparameters: {best_hyperparams}")
print(f"Best accuracy: {best_accuracy}")
从图中可以看出,不同的隐藏数和不同学习率之间,在准确率方面有很大的不同。