今天给大家讲解一下动态规划中的0-1背包问题，0-1背包问题是一个非常经典动态规划问题，题型很多，所以大家只有深入理解这个思路，才能在刷后面的相似背包问题的动态规划题目才会更加容易，如果大家看到不是很懂，建议多看几遍，也可以去看b站上其他博主的视频，总之这个在动态规划当中非常重要，大家一定要学会

题目描述： 

题目链接：52. 携带研究材料（第七期模拟笔试） (kamacoder.com)

题目描述：

小明是一位科学家，他需要参加一场重要的国际科学大会，以展示自己的最新研究成果。他需要带一些研究材料，但是他的行李箱空间有限。这些研究材料包括实验设备、文献资料和实验样本等等，它们各自占据不同的重量，并且具有不同的价值。

小明的行李箱所能承担的总重量是有限的，问小明应该如何抉择，才能携带最大价值的研究材料，每种研究材料可以选择无数次，并且可以重复选择。

输入描述：

第一行包含两个整数，n，v，分别表示研究材料的种类和行李所能承担的总重量 

接下来包含 n 行，每行两个整数 wi 和 vi，代表第 i 种研究材料的重量和价值

输出描述：

输出一个整数，表示最大价值。

输入示例：

4 5
1 2
2 4
3 4
4 5

输出示例：

10

示例分析： 

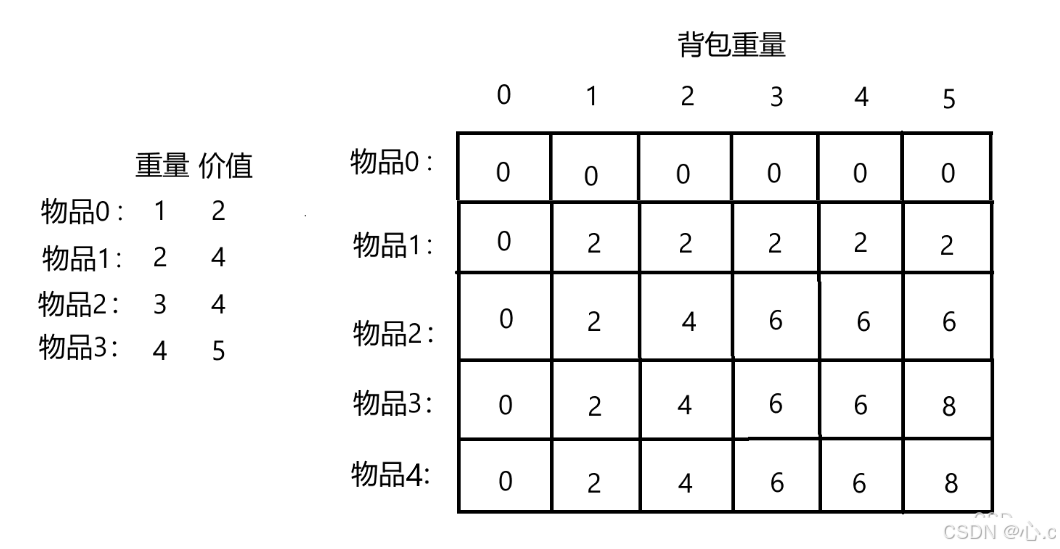
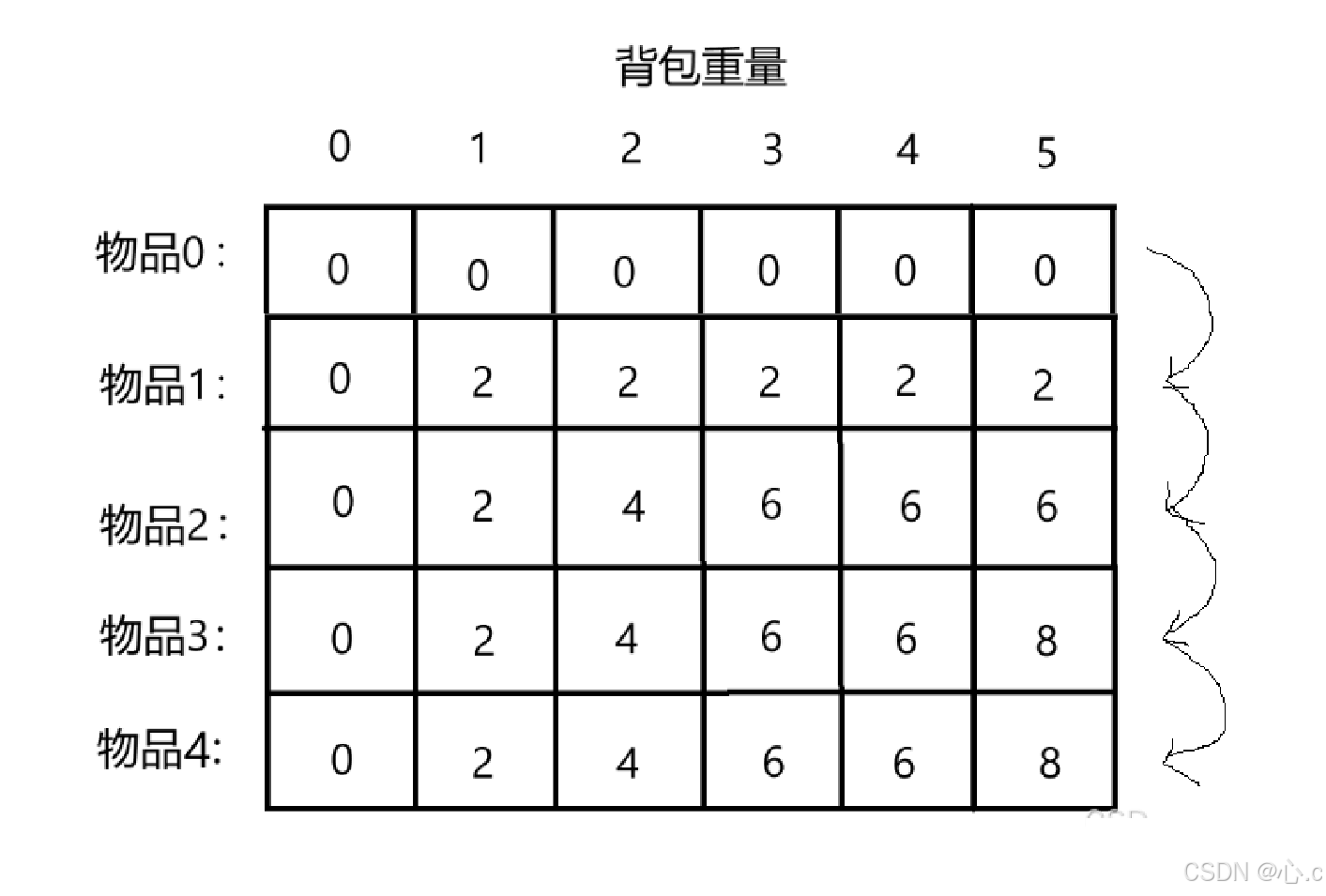
 二维背包代码及其分析：

二维0-1背包关于遍历顺序既可以先遍历物品，在遍历背包，也可以先遍历背包，再遍历物品，就是它的遍历顺序可以颠倒，不影响我们的dp数组，下面的代码我是先遍历的物品，然后再遍历背包

模拟实现过程：

现在我们开始从dp第二行进行遍历，就是我们的物品1，因为我们已经进行过初始化了

处理物品1：

当背包重量为0时，我们所储存的最大价值就是0（因为当背包容量为0时，装不了任何物品，所以我们的背包价值为0）

当背包重量为1时，我们进行当前物品与背包重量的判断，如果当前物品的重量大于等于背包，就是我们的背包可以装下该物品，我们就让背包装下该物品然后加上上一个物品在该剩余重量装下的价值和上一个物品的当前背包重量进行价值比较，装下最大的

当背包为2....5时，情况都是和上面的情况一样，所以在这里我就不赘述了

处理我们的物品2：

当背包重量为0时，我们所储存的最大价值就是0（这里就是我们的物品重量大于背包重量，所以我们使用的是物品0的时候对应背包重量为0时的最大价值）

当背包重量为1时，我们进行当前物品重量和背包重量比较，当前我们的物品重量为2，但是我们的背包重量只有1，所以我们没办法添加这个物品并且进行获取最大值的行为，所以我们还是获得物品0的当前背包重量的值的获取就是2

当背包重量为2时，我们进行当前物品重量和背包重量比较，当前我们的物品重量为2，然后背包重量也是2，所以我们可以将当前物品装入背包，然后剩余空间就是2-2=0，我们获取的就是上一个物品的剩余空间的最大价值加上我们当前的物品的价值，但是我们也要和上一个物品的当前背包中的价值进行比较，( 因为可能当前物品重量为99，然后价值为1，那其他的都是1：99....加上还不如不加，所以我们应该让当前价值和上一个背包的价值比较，得到最大的 )...............以此类推..................

先遍历物品再遍历背包

for(int i = 1; i < weight.size(); i++) { // 遍历科研物品
        for(int j = 0; j <= bagweight; j++) { // 遍历行李箱容量
            if (j < weight[i-1]) dp[i][j] = dp[i - 1][j]; 
            else {
                dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
            }
        }
    }

先遍历背包，再遍历物品 

    for(int j = 0; j <= bagweight; j++) { // 遍历行李箱容量         
          for(int i = 1; i < weight.size(); i++) { // 遍历科研物品
            if (j < weight[i-1]) dp[i][j] = dp[i - 1][j]; 
            else {
                dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
            }
        }
    }

 二维总代码：

 关于遍历顺序只需要颠倒一下for循环就可以了

#include <bits/stdc++.h>
using namespace std;

int main() {
    int n, bagweight;// bagweight代表行李箱空间
    cin >> n >> bagweight;
    vector<int> weight(n, 0); // 存储每件物品所占空间
    vector<int> value(n, 0);  // 存储每件物品价值
    for(int i = 0; i < n; ++i) {
        cin >> weight[i];
    }
    for(int j = 0; j < n; ++j) {
        cin >> value[j];
    }
   
    vector<vector<int>> dp(weight.size()+1, vector<int>(bagweight + 1, 0));

    for(int i = 1; i < weight.size(); i++) { // 遍历科研物品
        for(int j = 0; j <= bagweight; j++) { // 遍历行李箱容量
            if (j < weight[i-1]) dp[i][j] = dp[i - 1][j]; // 如果装不下这个物品,那么就继承dp[i - 1][j]的值
            else {
                dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
            }
        }
    }
    cout << dp[n - 1][bagweight] << endl;
    return 0;

}

一维背包代码及其分析：

一维和二维在思路上是差不多的，就是一维dp数组不断更新的过程一个不断更新的过程

不同点：

一维推荐先遍历物品再遍历背包，并且在遍历背包的时候必须是逆序，不然会导致一个物品被多次计算

逆序是为了让背包只能被选择一次，因为这是一维数组，我们使用的都是当前的值，如果正序，会导致背包对次选择该物品，大家可以举个例子就明白了

一维总代码：

#include <bits/stdc++.h>
using namespace std;

int main() {
    int n, bagweight; // bagweight代表行李箱空间
    cin >> n >> bagweight;
    vector<int> weight(n, 0); // 存储每件物品所占空间
    vector<int> value(n, 0);  // 存储每件物品价值
    for (int i = 0; i < n; ++i) {
        cin >> weight[i];
    }
    for (int j = 0; j < n; ++j) {
        cin >> value[j];
    }

    vector<int> dp(bagweight + 1, 0); // 一维数组，用于存储在不同背包容量下的最大价值

    for (int i = 0; i < n; ++i) { // 遍历每个物品
        for (int j = bagweight; j >= weight[i]; --j) { // 逆序遍历背包容量
            dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
        }
    }

    cout << dp[bagweight] << endl;
    return 0;
}