Bootstrap

算法.图论-习题全集(Updating)

文章目录

本节设置的意义

主要就是为了复习图论算法, 尝试从题目解析的角度,更深入的理解图论算法…

并查集篇

并查集简介以及常见技巧

并查集是一种用于大集团查找, 合并等操作的数据结构, 常见的方法有

  • find: 用来查找元素在大集团中的代表元素(这里使用的是扁平化的处理)
  • isSameSet: 用来查找两个元素是不是一个大集团的(其实就是find的应用)
  • union: 用来合并两大集团的元素

关于并查集打标签的技巧, 其实我们之前的size数组也是一种打标签的逻辑, 其实打标签就是给每一个集团的代表节点打上标签即可, 还有我们在并查集的题目中通常会设置一个sets作为集合的总数目(每次合并–), 这是一个常见的技巧, 并查集的细节我们在这里不进行过多的介绍, 在之前的章节中有细致的描述…

并查集板子(洛谷)

这里我们的并查集的板子使用的是洛谷的板子(小挂大的优化都没必要其实)

// 并查集模版(洛谷)
// 本实现用递归函数实现路径压缩，而且省掉了小挂大的优化，一般情况下可以省略
// 测试链接 : https://www.luogu.com.cn/problem/P3367

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;
import java.io.StreamTokenizer;

public class Main{

	public static int MAXN = 10001;

	public static int[] father = new int[MAXN];

	public static int n;

	public static void build() {
		for (int i = 0; i <= n; i++) {
			father[i] = i;
		}
	}

	public static int find(int i) {
		if (i != father[i]) {
			father[i] = find(father[i]);
		}
		return father[i];
	}

	public static boolean isSameSet(int x, int y) {
		return find(x) == find(y);
	}

	public static void union(int x, int y) {
		father[find(x)] = find(y);
	}

	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		StreamTokenizer in = new StreamTokenizer(br);
		PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
		while (in.nextToken() != StreamTokenizer.TT_EOF) {
			n = (int) in.nval;
			build();
			in.nextToken();
			int m = (int) in.nval;
			for (int i = 0; i < m; i++) {
				in.nextToken();
				int z = (int) in.nval;
				in.nextToken();
				int x = (int) in.nval;
				in.nextToken();
				int y = (int) in.nval;
				if (z == 1) {
					union(x, y);
				} else {
					out.println(isSameSet(x, y) ? "Y" : "N");
				}
			}
		}
		out.flush();
		out.close();
		br.close();
	}

}

情侣牵手问题

在这里插入图片描述
本题的突破点就是如果一个大集团里面有 n 对情侣, 那么我们至少要交换 n - 1次(通过把情侣进行编号)

// 这次我们尝试使用轻量版的并查集来解决这道题
class Solution {

    private static final int MAX_CP = 31;

    private static final int[] father = new int[MAX_CP];

    private static int sets = 0;

    private static int find(int i) {
        if (i != father[i]) {
            father[i] = find(father[i]);
        }
        return father[i];
    }

    private static boolean isSameSet(int a, int b) {
        return find(a) == find(b);
    }

    private static void union(int a, int b) {
        int fa = find(a);
        int fb = find(b);
        if (fa != fb) {
            father[fa] = fb;
            sets--;
        }
    }

    // 初始化并查集
    private static void build(int n) {
        for (int i = 0; i < n; i++) {
            father[i] = i;
        }
        sets = n;
    }

    public int minSwapsCouples(int[] row) {
        build(row.length / 2);
        for (int i = 0; i < row.length; i += 2) {
            int n1 = row[i] / 2;
            int n2 = row[i + 1] / 2;
            union(n1, n2);
        }
        return row.length / 2 - sets;
    }
}

相似的字符串组

在这里插入图片描述
其实就是枚举每一个位置, 然后判断是不是一组的就OK了

// 还是使用一下轻量级的并查集板子
class Solution {

    private static final int MAX_SZ = 301;

    private static final int[] father = new int[MAX_SZ];

    private static int sets = 0;

    private static int find(int i) {
        if (i != father[i]) {
            father[i] = find(father[i]);
        }
        return father[i];
    }

    private static boolean isSameSet(int a, int b) {
        return find(a) == find(b);
    }

    private static void union(int a, int b) {
        int fa = find(a);
        int fb = find(b);
        if (fa != fb) {
            father[fa] = fb;
            sets--;
        }
    }

    // 初始化并查集
    private static void build(int n) {
        for (int i = 0; i < n; i++) {
            father[i] = i;
        }
        sets = n;
    }

    public int numSimilarGroups(String[] strs) {
        build(strs.length);
        // 主流程的时间复杂度是 O(n ^ 2), 遍历strs的每一个位置
        int m = strs[0].length();
        for (int i = 0; i < strs.length; i++) {
            for (int j = i + 1; j < strs.length; j++) {
                // 获取到两个字符串, 然后计算两个字符串的不同字符数量
                String s1 = strs[i];
                String s2 = strs[j];
                int diff = 0;
                for (int k = 0; k < m && diff < 3; k++) {
                    if (s1.charAt(k) != s2.charAt(k))
                        diff++;
                }
                if (diff == 0 || diff == 2)
                    union(i, j);
            }
        }
        return sets;
    }
}

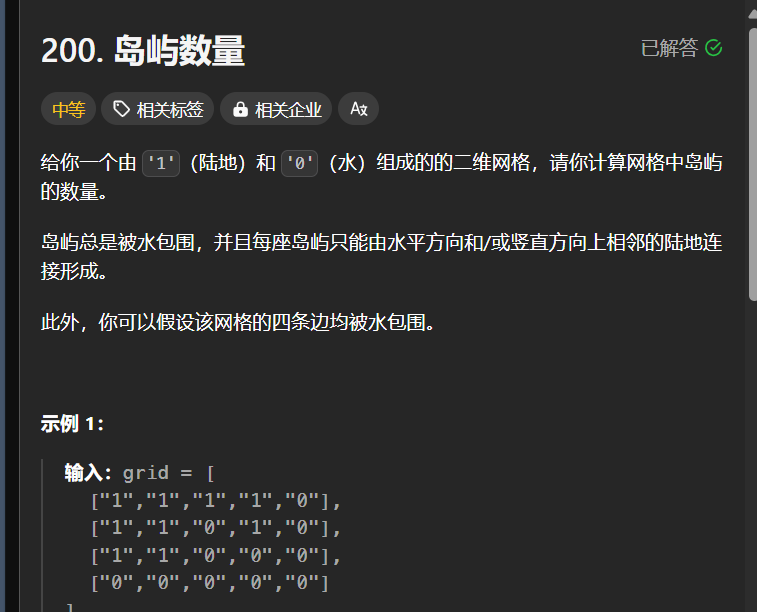
岛屿数量(并查集做法)

在这里插入图片描述
这道题的解法非常多, 比如多源 BFS , 洪水填充(其实就是递归加回溯) , 还有今天介绍的并查集的方法(这个方法不是最好的)

// 这个题的并查集做法只要注意一点就可以了: 把一个二维下标转化为一维下标
class Solution {

    private static final int MAX_SZ = 301 * 301;

    private static final int[] father = new int[MAX_SZ];

    private static int sets = 0;

    private static int row = 0;

    private static int col = 0;

    // 模拟bfs的move数组
    private static final int[] move = { -1, 0, 1, 0, -1 };

    private static int find(int i) {
        if (i != father[i]) {
            father[i] = find(father[i]);
        }
        return father[i];
    }

    private static boolean isSameSet(int a, int b) {
        return find(a) == find(b);
    }

    private static void union(int a, int b) {
        int fa = find(a);
        int fb = find(b);
        if (fa != fb) {
            father[fa] = fb;
            sets--;
        }
    }

    private static void build(char[][] grid, int rl, int cl) {
        row = rl;
        col = cl;
        sets = 0;
        for (int i = 0; i < row; i++) {
            for (int j = 0; j < col; j++) {
                if (grid[i][j] == '1') {
                    sets++;
                    father[getIndex(i, j)] = getIndex(i, j);
                }
            }
        }
    }

    public int numIslands(char[][] grid) {
        // 初始化并查集并统计 '1' 的数量
        build(grid, grid.length, grid[0].length);
        // 遍历grid进行合并
        for (int i = 0; i < row; i++) {
            for (int j = 0; j < col; j++) {
                // 向四个方向扩展
                if (grid[i][j] == '1') {
                    for (int k = 0; k < 4; k++) {
                        int nx = i + move[k];
                        int ny = j + move[k + 1];
                        if (nx >= 0 && nx < row && ny >= 0 && ny < col && grid[nx][ny] == '1') {
                            union(getIndex(i, j), getIndex(nx, ny));
                        }
                    }
                }
            }
        }
        return sets;
    }

    // 二维下标转一维下标
    private static int getIndex(int i, int j) {
        return i * col + j;
    }
}

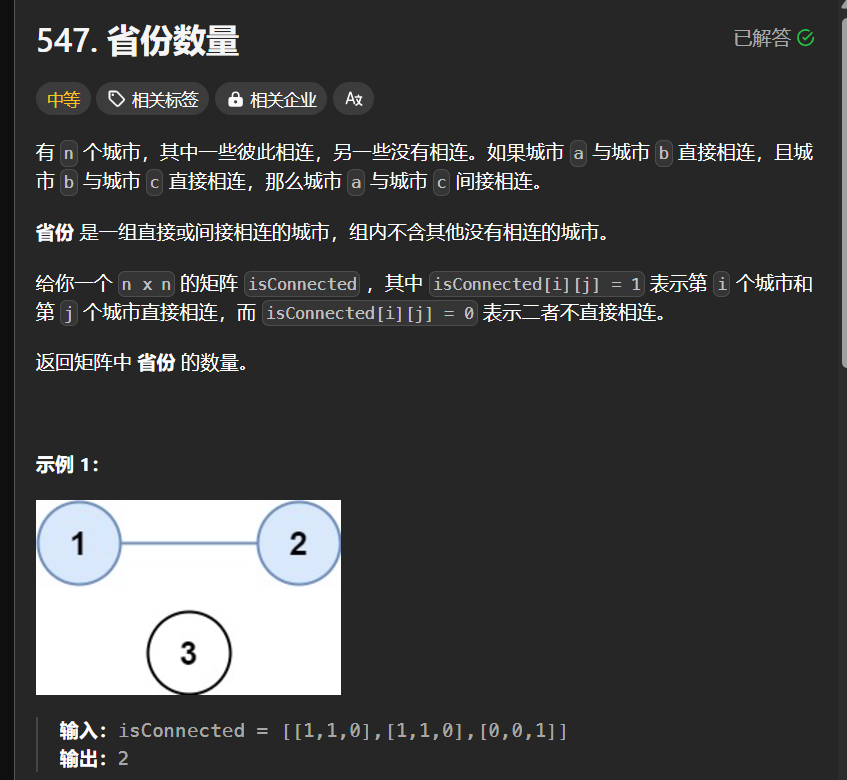
省份数量

在这里插入图片描述
没什么可说的, 就是一个简单的并查集的思路

class Solution {
    // 这其实也是一个并查集的题
    private static final int MAXM = 201;

    private static final int[] father = new int[MAXM];

    private static final int[] size = new int[MAXM];

    private static int sets = 0;

    private static int find(int i){
        if(i != father[i]){
            father[i] = find(father[i]);
        }
        return father[i];
    }

    private static boolean isSameSet(int a, int b){
        return find(a) == find(b);
    }

    private static void union(int a, int b){
        if(!isSameSet(a, b)){
            int fa = find(a);
            int fb = find(b);
            if(size[fa] > size[fb]){
                father[fb] = fa;
                size[fa] += size[fb];
            }else{
                father[fa] = fb;
                size[fb] += size[fa];
            }
            sets--;
        }
    }

    private static void build(int n){
        for(int i = 0; i < n; i++){
            father[i] = i;
            size[i] = 1;
        }
        sets = n;
    }

    public int findCircleNum(int[][] isConnected) {
        // 初始化并查集
        build(isConnected.length);

        for(int i = 0; i < isConnected.length; i++){
            int[] info = isConnected[i];
            for(int j = 0; j < info.length; j++){
                if(info[j] == 1){
                    union(i, j);
                }
            }
        }

        return sets;
    }
}

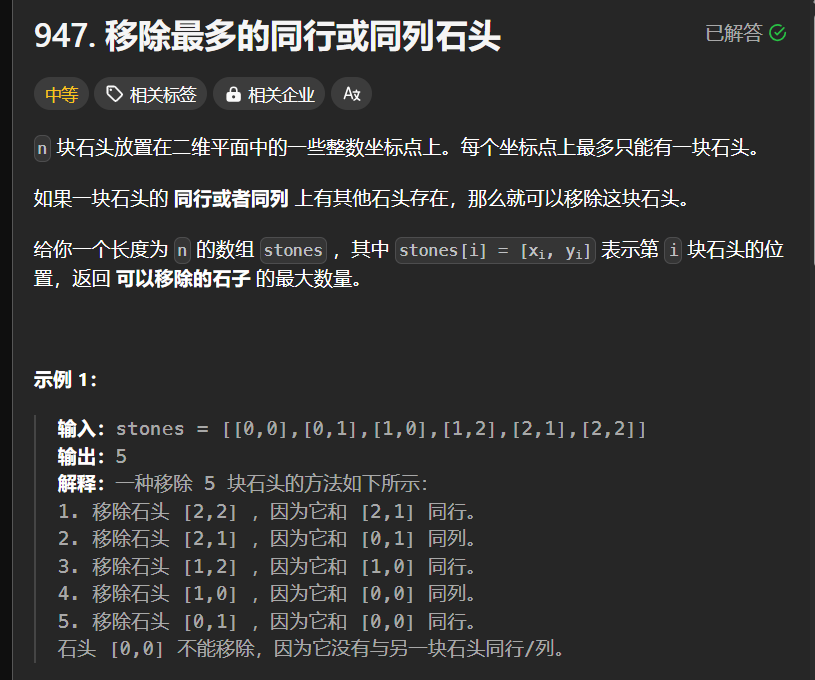
移除最多的同行或同列石头

在这里插入图片描述
其实就是每一个集团最后都会被消成一个元素, 我们中间用哈希表加了一些关于离散化的处理的技巧

// 使用一下轻量版本的并查集加上哈希表进行离散化的操作
class Solution {

    private static Map<Integer, Integer> rowFirst = new HashMap<>();
    
    private static Map<Integer, Integer> colFirst = new HashMap<>();

    private static final int MAXM = 1001;

    private static final int[] father = new int[MAXM];

    private static int sets = 0;

    private static int find(int i){
        if(i != father[i]){
            father[i] = find(father[i]);
        }
        return father[i];
    }

    private static boolean isSameSet(int a, int b){
        return find(a) == find(b);
    }

    private static void union(int a, int b){
        int fa = find(a);
        int fb = find(b);
        if(fa != fb){
            father[fa] = fb;
            sets--;
        }
    }

    // 初始化并查集
    private static void build(int n){
        for(int i = 0; i < n; i++){
            father[i] = i;
        }
        sets = n;
    }

    public int removeStones(int[][] stones) {
        // 清空哈希表
        rowFirst.clear();
        colFirst.clear();
        // 初始化并查集
        build(stones.length);
        for(int i = 0; i < stones.length; i++){
            int row = stones[i][0];
            int col = stones[i][1];
            if(!rowFirst.containsKey(row)){
                rowFirst.put(row, i);
            }else{
                union(rowFirst.get(row), i);
            }
            if(!colFirst.containsKey(col)){
                colFirst.put(col, i);
            }else{
                union(colFirst.get(col), i);
            }
        }
        return stones.length - sets;
    }
    
}

悦读

道可道，非常道；名可名，非常名。 无名，天地之始，有名，万物之母。 故常无欲，以观其妙，常有欲，以观其徼。 此两者，同出而异名，同谓之玄，玄之又玄，众妙之门。

最新收录
elementUI cascader 删除事件
JS统计一个字符串中数字字符的个数。
音视频开发—使用FFmpeg将YUV文件编码成H264裸流文件 C语言实现
SpringBoot整合SSS框架+sessionId已一致性
AI绘画 | 手把手教你安装SD插件controlnet
ROS平台下INDEMIND双目惯性模组SDK教程 原创
webpack进阶(二)
json在后台封装后，返回中文乱码
【国产开源可视化引擎Meta2d.js】锚点
Python教程：一文掌握Python多线程（很详细）
;