本篇博客给大家带来的是子序列问题之动态规划解法技巧.
🐎文章专栏: 动态规划
🚀若有问题 评论区见
❤ 欢迎大家点赞 评论 收藏 分享
如果你不知道分享给谁,那就分享给薯条.
你们的支持是我不断创作的动力 .

要开心

要快乐

顺便进步

1. 最长递增子序列

题目链接: 300. 最长递增子序列

题目内容:

给你一个整数数组 nums ，找到其中最长严格递增子序列的长度。

子序列 是由数组派生而来的序列，删除（或不删除）数组中的元素而不改变其余元素的顺序。例如，[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。

示例 1：

输入：nums = [10,9,2,5,3,7,101,18]
输出：4
解释：最长递增子序列是 [2,3,7,101]，因此长度为 4 。
示例 2：

输入：nums = [0,1,0,3,2,3]
输出：4
示例 3：

输入：nums = [7,7,7,7,7,7,7]
输出：1

提示：

1 <= nums.length <= 2500
-10^4 <= nums[i] <= 10^4

做题先知

第一 步骤分析

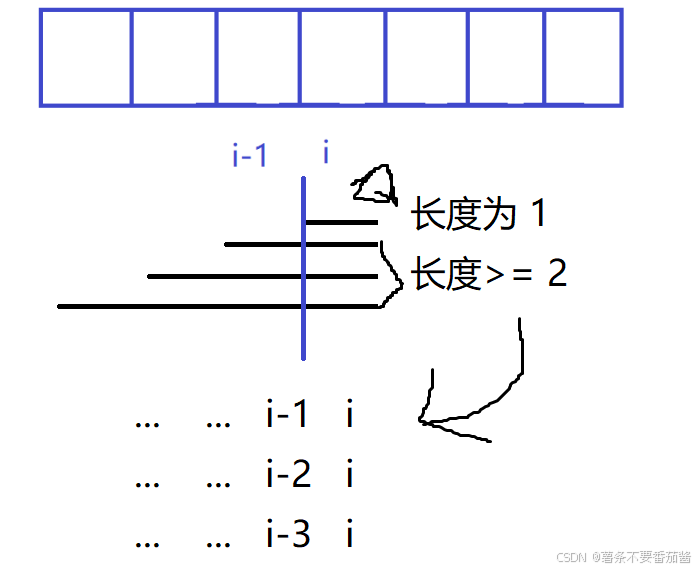
1. 状态表示
按通用的形式: 以 i 位置为结尾 … 来定义
dp[i] 表示 以 i 位置为结尾所有子序列中, 最长严格递增子序列的长度.

2. 状态转移方程
从最后一个位置分情况: 子序列可能只是 nums[i] 即长度为1, 也可能大于等于2.

当长度等于1时, dp[i] = 1;
当长度 >= 2时, 子序列的组成有很多种情况, 定义变量 j (0<= j <=i), 如果 nums[j] < nums[i]; dp[i] = Math.max(dp[i],dp[j] + 1); dp[i] 只取dp[j] 最长的那个值.

3. 初始化
在对求长度的题中, 我们通常都是将整个dp表全部初始化为 状态转移方程中的最小情况. 本题初始化为 1 , 因为 nums至少有1个元素, 子序列至少为1.

4. 填表顺序
从左往右填写

5. 返回值
根据dp[i]的定义可知,dp[i]存储的是 i 位置为结尾的递增子序列长度最大值, 但是最大值中仍然有更大的, 所以应该返回的是dp表中的最大值.

第二 代码实现

class Solution {
    public int lengthOfLIS(int[] nums) {
        int n = nums.length;
        int ret = -Integer.MAX_VALUE;
        //1.创建dp表
        int[] dp = new int[n];
        //2.初始化
        if(n == 1) return 1;
        for(int i = 0;i < n;++i) {
            dp[i] = 1;
        }
        //3. 填表
        for(int i = 1;i < n;++i) {
            for(int j = 0;j < i;++j) {
                if(nums[j] < nums[i]) {
                    dp[i] = Math.max(dp[i],dp[j]+1);
                }
            }
            ret = Math.max(ret,dp[i]);
        }
        return ret;
    }
}

2. 最长递增子序列的个数

题目链接: 673. 最长递增子序列的个数

题目内容:

给定一个未排序的整数数组 nums ， 返回最长递增子序列的个数 。

注意 这个数列必须是 严格 递增的。

示例 1:

输入: [1,3,5,4,7]
输出: 2
解释: 有两个最长递增子序列，分别是 [1, 3, 4, 7] 和[1, 3, 5, 7]。
示例 2:

输入: [2,2,2,2,2]
输出: 5
解释: 最长递增子序列的长度是1，并且存在5个子序列的长度为1，因此输出5。

提示:

1 <= nums.length <= 2000
-10^6 <= nums[i] <= 10^6

第一 先介绍一个小算法,求数组最大值个数

第二 动态规划

1. 状态表示
常规定义: dp[i] 表示 … 的最长长度的个数. 但是问题是最长的长度是多少都不知道,个数自然求不了.
本题的正确定义:
len[i] 表示以 i 位置为结尾的所有子序列中,递增子序列的最长"长度".
count[i] 表示以 i 位置为结尾的所有子序列中, 递增子序列最长长度的个数.

2. 状态转移方程
len[i]的分析过程与上一道题一样, 这里便不再单独做len[i]分析,直接和count[i]一起分析
当长度为1时, count[i] = len[i] = 1;
当长度大于1时, 定义变量 j (0<= j < i), 在nums[j] < nums[i]严格递增的条件下,又可分为三种情况:
len[j]+1 == len[i], count[i] += count[j];
len[j]+1 < len[i], 不做任何动作;
len[j]+1 > len[i], len[i] = len[j]+1; count[i] = count[j];

3. 初始化
将count表和len表全部初始化为1.

4. 填表顺序
从左往右同时填写.

5. 返回值
拿到 长度len表 和 个数count之后,继续求len表中最大值的个数. 然后返回.

第三 代码实现

class Solution {
    public int findNumberOfLIS(int[] nums) {
        int n = nums.length;
        //1. 建dp表
        int[] len = new int[n];
        int[] count = new int[n];
        //2. 初始化
        for(int i = 0;i < n;++i) {
            len[i] = count[i] = 1;
        }
        int retlen = 1;
        int retcount = 1;
        //3. 填表
        for(int i = 1;i < n;++i) {
            for(int j = 0;j < i;++j) {
                // if(nums[j] < nums[i]) {
                //     len[i] = Math.max(len[j]+1,len[i]);
                // }
                if(nums[j] < nums[i]) {
                    if(len[j]+1 == len[i]) {
                    count[i] += count[j];
                }else if(len[j]+1 > len[i]) {
                    len[i] = len[j] + 1;
                    count[i] = count[j];
                }
                }
            }
            if(retlen == len[i]) {
                retcount += count[i];
            }else if(retlen < len[i]) {
                retlen = len[i];
                retcount = count[i];
            }
        }
        return retcount;
    }
}

本篇博客到这里就结束啦, 感谢观看 ❤❤❤

🐎期待与你的下一次相遇😊😊😊