题目描述

原题：142. 环形链表 II
前面我们探究了如何判断环形链表：
ListOJ13：环形链表(判断是否为环形链表)
那我们如何找到这个环的入口点呢？我们先来看看这题OJ：

思路分析

思路一

第一种思路简单：

由上篇：
ListOJ13：环形链表(判断是否为环形链表)
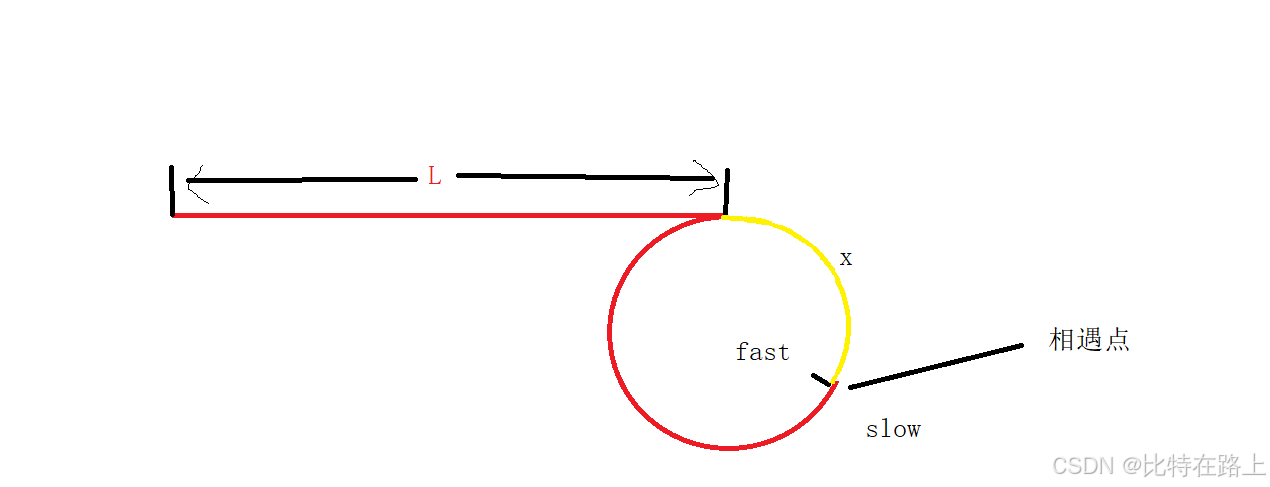
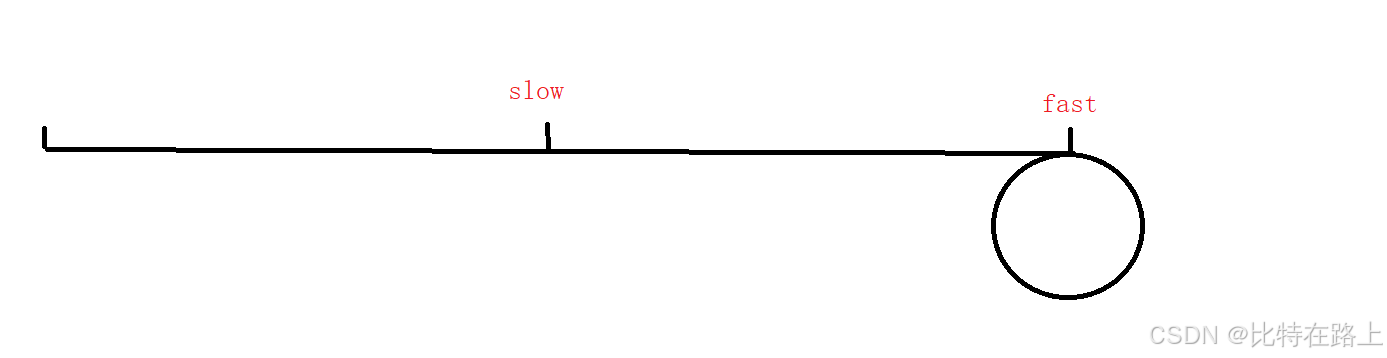
我们得知，环形链表中的快慢指针一定会相遇的：

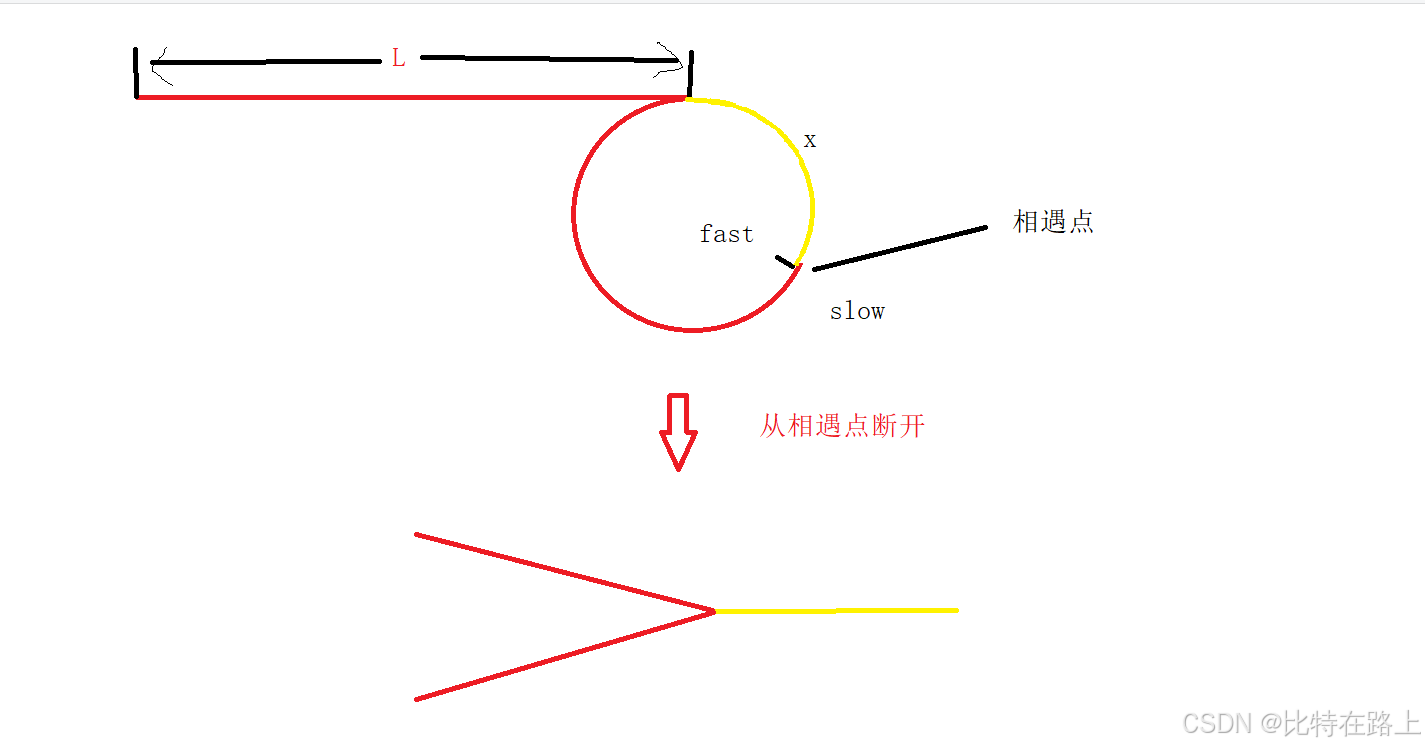
这时候我们将环从相遇点断开：

那问题转化为求相交链表的相交点了：
这个问题我们在这篇博客已经详细讨论过了：
160. 相交链表

这里不多加赘述：代码在下面展示；

思路二

这个思路写起来很简单，但是理解起来相对难；
我们先来看代码：

typedef struct ListNode ListNode;
struct ListNode* detectCycle(struct ListNode* head) {
    ListNode* fast, * slow;
    fast = slow = head;
    while (fast && fast->next)
    {
        slow = slow->next;
        fast = fast->next->next;
        if (slow == fast)
            break;
    }
    if (fast == NULL || fast->next == NULL)
    {
        return NULL;
    }
    ListNode* meet = fast;
    while (head != meet)
    {
        head = head->next;
        meet = meet->next;
    }
    return meet;
}

这个代码不难理解：

1、用指针meet指向链表的快慢指针相遇的节点；
2、同时移动meet指针和头指针；
3、当两个指针指向同一个节点时，该节点就是环的入口点。

证明

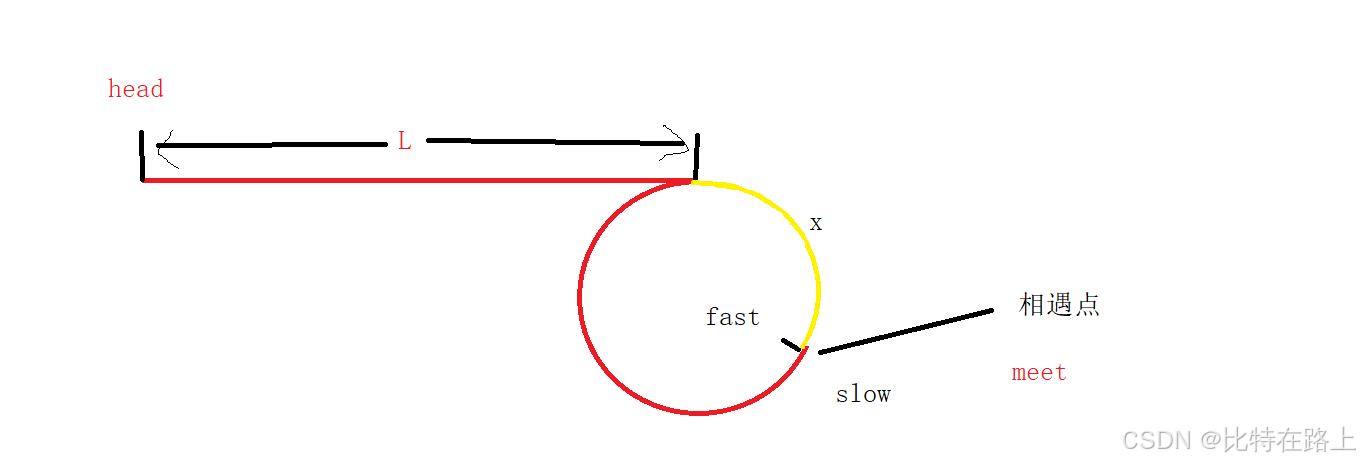
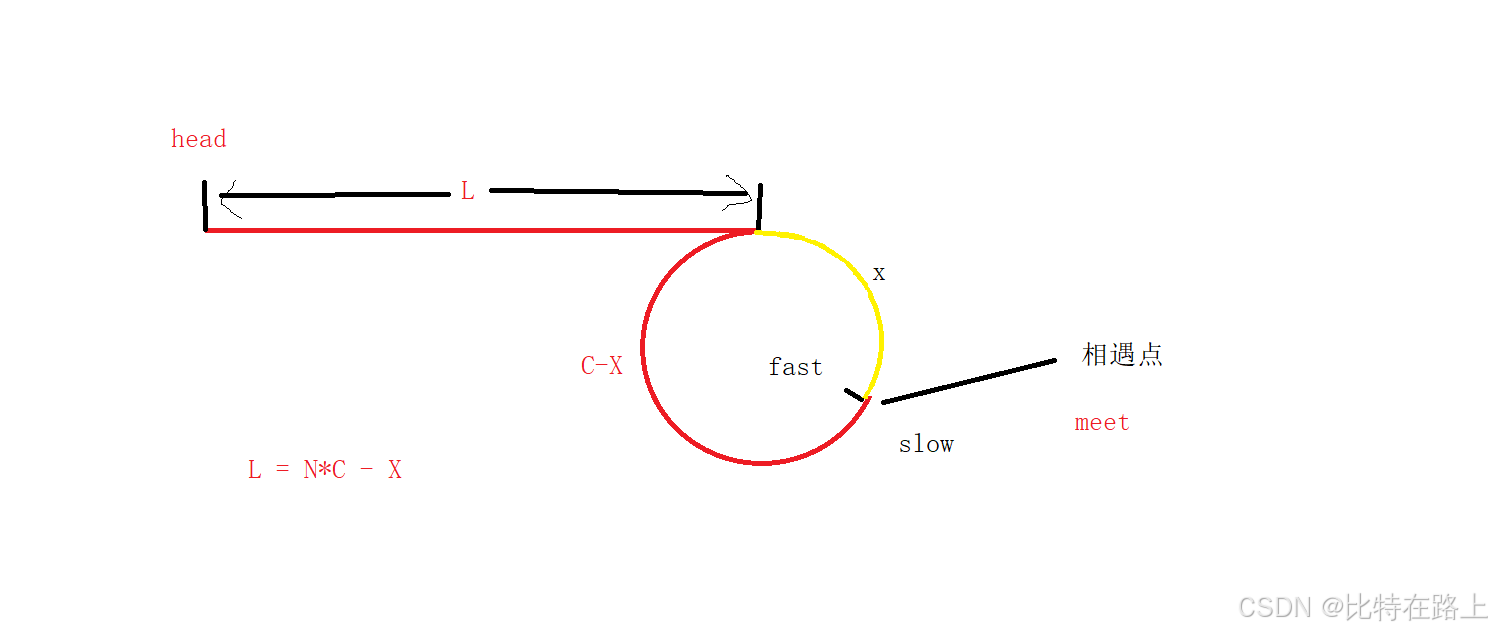
（设环的长度为C）当慢指针slow到达相遇点时，slow走过的距离设为L+X，则快指针fast走过的距离为L+X+N*C （N是slow为到达环入口点时，fast所走过环的圈数， N大于等于1）

为什么slow走过的距离是 L+X， 而不是L+X+圈数?

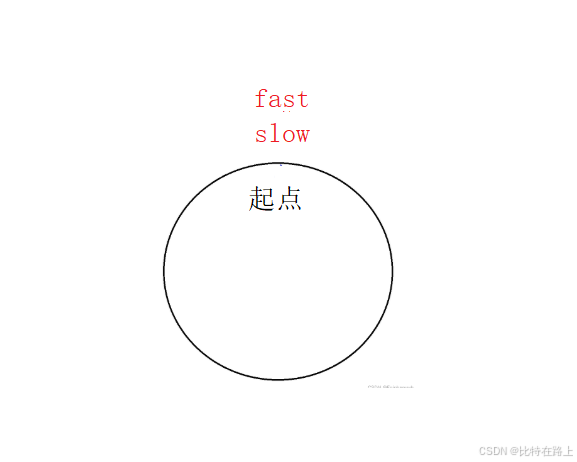
我们来看看slow走最大的路程的情况：

此时，slow走一圈fast走两圈追上slow：

由于走过前面 L长度的节点后，fast和slow之间一定有距离，所以当slow到达环的入口点时，fast可能不在环的入口点，所以slow肯定不会走一圈的。

fast走过的距离为什么是 L+X+N*C，为什么不是L+X+N,并且N大于等于1？

这里我解释一下 “N*C，并且N大于等于1”，由于slow一次移动一个节点，fast一次移动两个节点，相同的时间下，fast的速度大于slow的速度，两者走过的距离肯定不相同，所以在fast走第一圈内，slow和fast不会相遇，只有当fast超过slow一圈或几圈后，两者才能相遇。

或者我们这样理解，但L远远大于C时：

此时fast就不止走一圈了；

又因为fast走过的距离是slow走过距离的二倍，所以有：

L+X+NC = 2（L+X）
即 L = N*C - X

也就是说相遇点meet和head同时向后走，一定会在环的入口处相遇：
由此我们得出结论；

代码展示

思路一：转化为寻找相交节点的相交点处：

struct ListNode* getIntersectionNode(struct ListNode* headA, struct ListNode* headB)
{
    if(headA==NULL && headB==NULL)
    {
        return NULL;
    }
    struct ListNode* curA = headA, * curB = headB;
    int count1 = 0, count2 = 0;
    while (curA->next != NULL)
    {
        count1++;
        curA = curA->next;
    }
    while (curB->next != NULL)
    {
        count2++;
        curB = curB->next;
    }
    int gap = abs(count1 - count2);
    struct ListNode* longlist = headA;
    struct ListNode* shortlist = headB;
    if (count1 < count2)
    {
        longlist = headB;
        shortlist = headA;
    }
    if (curB == curA)
    {
        while (gap--)
        {
            longlist = longlist->next;
        }
        while (longlist != shortlist)
        {
            longlist = longlist->next;
            shortlist = shortlist->next;
        }
        return longlist;
            
    }
    else
    {
        return NULL;
    }
}
 
struct ListNode* getmeetnode(struct ListNode* head)
{
    struct ListNode* fast, * slow;
    fast = slow = head;
    while (fast && fast->next)
    {
        fast = fast->next->next;
        slow = slow->next;
        if (fast == slow)
        {
            return fast;
        }
    }
    return NULL;
}
struct ListNode* detectCycle(struct ListNode* head)
{
    // 找到相遇点
    
    struct ListNode* meetnode = getmeetnode(head);
    if(meetnode == NULL)
    {
        return NULL;
    }
    // 断开为两个链表
    struct ListNode* cur1, *cur2;
    cur1 = meetnode->next;
    meetnode->next=NULL;
    cur2 = head;
 
    // 找到两个链表的交点
    struct ListNode* IntersectionNode = getIntersectionNode(cur1, cur2);
    return IntersectionNode;
 
}

思路二：利用数学推理巧妙的解决：

typedef struct ListNode ListNode;
struct ListNode* detectCycle(struct ListNode* head) {
    ListNode* fast, * slow;
    fast = slow = head;
    while (fast && fast->next)
    {
        slow = slow->next;
        fast = fast->next->next;
        if (slow == fast)
            break;
    }
    if (fast == NULL || fast->next == NULL)
    {
        return NULL;
    }
    ListNode* meet = fast;
    while (head != meet)
    {
        head = head->next;
        meet = meet->next;
    }
    return meet;
}

这两种方法都是可以通过leetcode的：

完