本节来讨论一下一个用于生成多孔介质几何模型的方法-quartet structure generation set (QSGS)方法。

本文提出了一种更全面的方法，其中确定了四个参数来控制颗粒介质的内部多孔结构，从而形成了一个称为四重结构生成集（QSGS）的集合。该集合使我们能够生成类似于许多实际多孔介质形成过程的多孔形态特征。

1. 算法描述

（1）确定生长相和非生长相：

• 在开始之前，需要在系统中的不同相中确定一个非生长相，其余为生长相。通常情况下，离散相被视为生长相。例如，在未饱和砂中，岩石和湿气是生长相（在未饱和砂中，非生长相通常是空气（或气体）。岩石和湿气（液体）是生长相，而空气作为不参与生长过程的非生长相。）；而在聚氨酯泡沫中，气体是生长相。

（2）在网格系统中随机定位第一生长相的核心：

• 基于核心分布概率 ​，随机在网格中定位第一生长相的核心。每个网格单元将被分配一个在0到1之间的随机数。随机数不大于  的单元将被选为核心。

（3）扩展生长相的每个元素：

• 根据每个方向的定向生长概率 ，将生长相的每个元素向其所有方向的邻近单元扩展。新的随机数将分配给这些邻近单元。如果邻近单元的随机数不大于 ，它将成为生长相的一部分。

（4）检查第一生长相的体积分数是否达到给定值 ：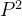

• 如果生长相是气体，通常表示为孔隙率 。如果尚未达到给定值，则重复步骤3；如果已达到，则继续下一步。

（5）处理下一生长相：

• 对于每个新的生长相，首先考虑其与现有生长相的相互作用。如果新的生长相与现有相类似，例如多组分混合物，则从独立的种子生长，这与第一生长相的生长过程相似。
• 否则，需要考虑与现有相的相互作用约束。根据相互作用生长概率​，新的生长相在特定方向上生长。

（6）停止生长相的生长：

• 若当前生长相的体积分数达到给定值  时，停止该相的生长。

（7）重复步骤5和6：

• 按照上述步骤处理每个新的生长相，直到所有相都达到各自的体积分数。

（8）生成最终结构：

• 所有未被占据的空间代表非生长相。输出最终的多孔介质结构数据。

想必大家阅读完算法描述后脑海中依旧没有形成形象化的生长方法，don't worry，请继续往后看，接下来先解答第一批疑惑：

1. 什么是核心分布概率？

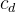
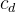
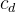
核心分布概率  是指一个单元成为第一生长相核心的概率。核心是生长相开始生长或扩展的初始点。​ 的值表示第一生长相的生长核心的数量密度，用来反映整个系统中第一生长相的统计分布。例如，如果在一个200×200的网格中有40个核心，那么 值为40/40000=0.001，这意味着每个网格单元有0.001的概率成为核心。

2. 什么是定向生长概率？

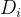
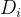
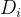
比如我们从一个核心网格开始，有8个方向向四周生长，我们会为每个方向设定一个概率值（通常为0-1之间），在每一个时步，我们都会通过取随机数的方式为每个方向取一个随机概率，如果随机概率值≤预设的，将会在该方向“长”出一个新的网格。如果随机数大于定向生长概率 ​，则该邻近单元不会成为生长相的一部分。

然后对于新长出的网格，我们依旧按照这个方式来生成新的网格。比如某个网格的向1方向生成了一个网格，那么在下一个时步会在该网格上继续向周围几个方向生长。

假设我们有一个二维网格系统，其中每个网格单元有八个邻近单元：

• 各向同性生长：

  • 设定所有方向上的 值相同，例如 D1​=D2​=D3​=D4​=D5​=D6​=D7​=D8​=0.3。这意味着每个方向上的生长概率都是0.3，生长过程没有特定的方向性。

• 各向异性生长：

  • 设定某些方向上的 值较高，而其他方向上的​  值较低。例如：
    • 水平方向（1和3方向）的生长概率较高，设为 D1=D3=0.5。
    • 垂直方向（2和4方向）的生长概率较低，设为 D2=D4=0.2。
    • 对角方向（5到8方向）的生长概率设为中间值 D5=D6=D7=D8=0.3。

3.文中，和并不是指数学上的次方，而是表示表示第 n 个生长相的目标体积分数。

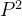
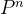
4. 在算法描述中，什么时候需要用到相互作用生长概率？如何用？

在多相多孔介质生成的算法描述中，相互作用生长概率 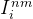是在多个相之间的生长过程中使用的，特别是在有多个生长相（例如液体和固体）同时生长时。

举例：

①处理液体相的生长：

• 对于液体相的每个生长网格，在每个方向上选择目标网格。
• 如果目标网格是固体相，则生成随机数并与相互作用生长概率比较，决定是否覆盖固体并生长为液体。
• 如果目标网格不是固体相，则直接生成随机数并与生长概率比较，决定是否生长为液体。

②处理固体相的生长：

• 对于固体相的每个生长网格，在每个方向上选择目标网格。
• 如果目标网格是液体相，则生成随机数并与相互作用生长概率比较，决定是否覆盖液体并生长为固体。
• 如果目标网格不是液体相，则直接生成随机数并与生长概率比较，决定是否生长为固体。

B. 所生成的一些case.

图1：8个方向的概率分别为0.1 0.1 0.1 0.1 0.2 0.05 0.2 0.05；设定的随机生成种子的概率为2%，domain的尺寸是200*200，设定的固相分数为60%。采用Disk腐蚀（Erosion）方法优化原始生成的图像，腐蚀 是一种形态学操作，它会缩小图像中的高亮（白色）区域，并扩大低亮（黑色）区域。它的基本思想是用一个结构元素扫描图像，并在结构元素完全包含在目标区域内时保留中心像素，否则移除中心像素。

Specifical steps:

• 生成结构元素： 通过 strel('disk', radius) 创建一个半径为 radius 的圆盘形结构元素。radius 可以是1、2、3等不同值。
• 应用腐蚀操作： 使用 MATLAB 的 imerode 函数对图像进行腐蚀。该函数将结构元素应用于图像的每个像素，按照结构元素的形状检查周围的像素，并执行腐蚀操作。
• 效果： 随着结构元素半径的增加，图像中的白色区域会逐渐缩小，黑色区域会逐渐扩大。这个过程可以用来去除图像中的小噪声，或在多孔介质中模拟颗粒的磨损。

Detailed information about Fig. 1: 

原始图像的孔隙率: 0.399975, 固相体积分数: 0.600025, 总和: 1.000000;
使用disk(1)腐蚀后图像的孔隙率: 0.604125, 固相体积分数: 0.395875, 总和: 1.000000;
使用disk(2)腐蚀后图像的孔隙率: 0.766975, 固相体积分数: 0.233025, 总和: 1.000000;
使用disk(3)腐蚀后图像的孔隙率: 0.882425, 固相体积分数: 0.117575, 总和: 1.000000.

图2：8个方向的概率分别为0.1 0.1 0.1 0.1 0.2 0.05 0.2 0.05；设定的随机生成种子的概率为2%，domain的尺寸是200*200，设定的固相分数为60%。采用中值滤波（Median Filtering）优化原始生成的图像，中值滤波 是一种非线性滤波技术，常用于去除图像中的噪声。它通过用像素邻域的中值代替中心像素的值来去除噪声，特别适用于去除椒盐噪声。

Specifical steps:

• 定义滤波器窗口大小： 通过设置 kernel 参数来定义中值滤波器的窗口大小（如2x2、3x3、4x4等）。
• 应用中值滤波： 使用 MATLAB 的 medfilt2 函数对图像进行中值滤波。该函数会将每个像素替换为其邻域像素值的中值。
• 效果： 随着滤波器窗口大小的增加，图像中的噪声会被更强烈地抑制，但也可能导致一些细节的丢失。

Detailed information about Fig. 2: 

使用medfilt2 kernel=2的图像孔隙率: 0.440375, 固相体积分数: 0.559625, 总和: 1.000000;
使用medfilt2 kernel=3的图像孔隙率: 0.383700, 固相体积分数: 0.616300, 总和: 1.000000;
使用medfilt2 kernel=4的图像孔隙率: 0.398675, 固相体积分数: 0.601325, 总和: 1.000000;

参考文献：Wang M , Wang J , Pan N , et al. Mesoscopic predictions of the effective thermal conductivity for microscale random porous media.[J]. Physical Review E Statistical Nonlinear & Soft Matter Physics, 2007, 75(3):036702.

如有错误，请评论区批评指正。

良心创作，转载请注明出处----CFD龙猫