1、 题目描述

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

2、解题思路

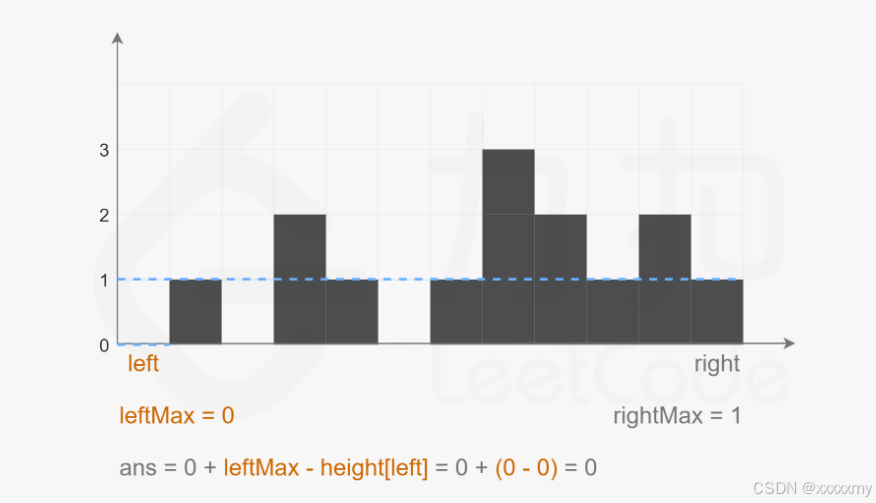
本题使用了双指针，根据下图可以得出，下标 i 处能接的雨水量由左边最大值 leftMax 和右边最大值 rightMax 中的最小值决定，因此设置左指针left和右指针right，左指针只会向右移动，右指针只会向左移动，遍历的过程中持续更新 leftMax 和 rightMax 。

• 若 leftMax < rightMax，下标 left 处能接的雨水量等于 leftMax−height[left]，将下标 left 处能接的雨水量加到能接的雨水总量，然后将 left 加 1（即向右移动一位）
• 若 leftMax ≥ rightMax，下标 right 处能接的雨水量等于 rightMax−height[right]，将下标 right 处能接的雨水量加到能接的雨水总量，然后将 right 减 1（即向左移动一位）

class Solution {
    public int trap(int[] height) {
        // 定义左右指针
        int left=0,right=height.length-1;
        // 定义左边最大值和右边最大值
        int leftMax=0,rightMax=0;
        // 定义最终结果
        int ans = 0;

        // 两个指针相遇为循环结束条件
        while(left<right){
            // 判断当前高度是否比最大高度大，若是，更新最大高度
            if(height[left]>leftMax)
                leftMax = height[left];
            if(height[right]>rightMax)
                rightMax = height[right];

            // 下标i处能接到的雨水量由leftMax和rightMax的最小值决定
            if(leftMax<rightMax){
                ans += leftMax-height[left];
                left++;
            }
            else{
                ans += rightMax-height[right];
                right--;
            }
        }

        return ans;
    }
}

• 时间复杂度：O(n)，其中 n 是数组 height 的长度。两个指针的移动总次数不超过 n。
• 空间复杂度：O(1)。只需要使用常数的额外空间。