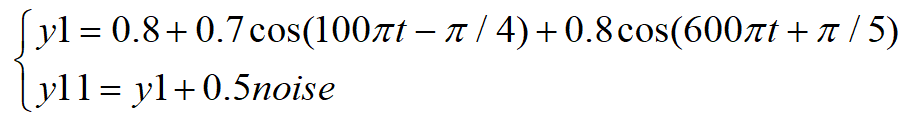本文介绍信号频域分析中功率谱和功率谱密度(PSD)的相关代码和分析过程,该功率谱和功率谱密度采用的是非参数法中的周期图法。本文提供功率谱和功率谱密度的封装函数,但还是推荐使用Matlab的periodogram函数。
1.理论介绍
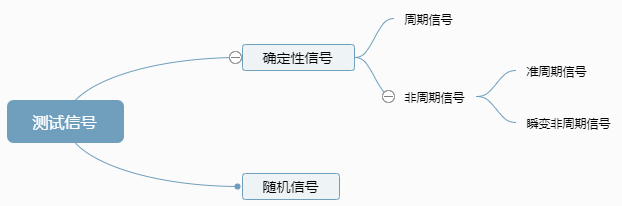
功率谱和功率谱密度是针对随机信号而言,关于信号分类的定义如下图:
确定性信号:可以表示为一个确定的时间函数,因而可确定其任何时刻的量值,这种信号称为确定性信号。
周期信号:按照一定时间间隔周而复始重复出现,无始无终的信号。
非周期信号:不具有周期重复性的信号。
准周期信号:两种以上的周期信号合成的,但其组成分量间无法找到公共周期,因而无法按某一时间间隔周期而重复出现的信号。
瞬变非周期信号:除准周期信号之外的其他非周期信号,是一些或在一定时间区间内存在,或随着时间的增长而衰减至零的信号。
随机信号:一种不能准确预测其未来瞬时值,也无法用数学关系式来描述的信号。但是具有某些统计特征,可以用概率统计方法由其过去来估计其未来。例如噪声信号、含噪信号,工程中没有绝对意义的无噪信号,可使用功率谱和功率谱密度分析。
对随机信号按照历程所作的各次长时间观测记录成为样本函数。在同一试验条件下,全部样本函数的集合就是随机过程。随机过程有平稳过程和非平稳过程之分,平稳随机过程是指其统计特征参数不随时间而变化的随机过程,否则为非平稳随机过程。
在平稳随机过程中,若任一单个样本函数的时间平均统计特征等于该过程的集合平均统计特征,这样的平稳随机过程叫各态历经随机过程。工程中,很多随机信号分析时我们都前提认为所取信号具有各态历经性,有的虽然不满足严格的各态历经过程,但可以忽略那些不具有各态历经性分量,它们可能不是重点研究对象。
随机信号在时间上是无限的,因此是能量无限、功率有限的信号。而能量无限的信号不满足傅里叶变换绝对可积条件。因此随机信号的傅里叶变换是不存在的,但是随机信号的功率是有限的,采用功率谱可以从统计的角度来描述随机信号的频域特性。
2.具体案例
周期图法绘制信号的功率谱,就是取一段有限长的信号进行傅里叶变换然,然后取模的平方,再除以信号的长度。这里有一个含噪信号y11,表达式如下:
noise表示一个符合标准正态分布的随机噪声,采样频率设置为1000,信长度为2000,即信号的时间长度为2s。上述这个信号的时域波形如下图所示:
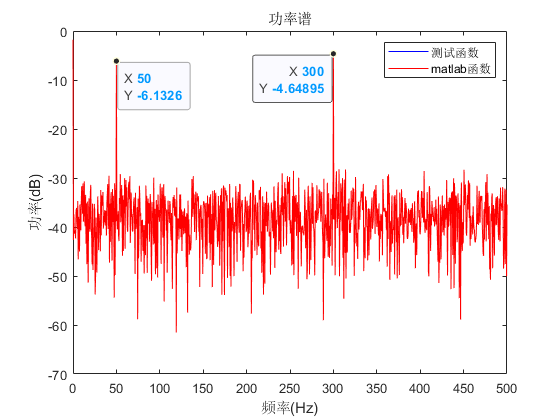
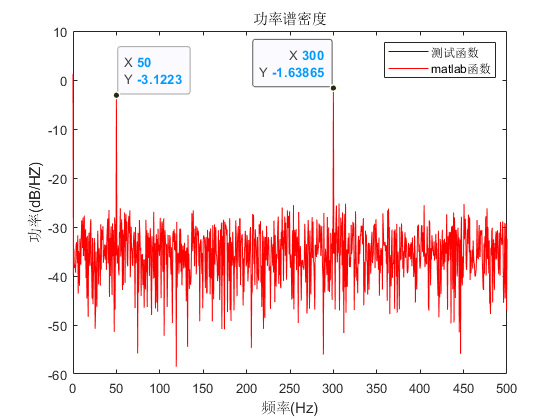
上图信号的功率谱和功率谱密度如下图所示:
无论是从上述功率谱和功率谱密度中,都能发现信号中存在两个突出的频率分量50Hz和300Hz。幅值数值的意义需要比较不同信号才有价值,实际分析信号时一般都只看功率谱密度。
需要注意的是,上述功率谱和功率谱密度画图时采用pow2db函数,将功率转换为了分贝数,关系式为:ydb=10log10(y)。周期图法中,功率谱和功率谱密度的区别在于,功率谱密度是功率谱再除以采样频率fs,可以理解为去除采用频率差异的影响,所以功率谱和功率谱密度的单位分别为dB和dB/Hz。
除此之外,值得注意的是该图中有两条曲线,一条蓝色的一条红色的,蓝色为测试函数,红色为matlab的periodogram函数,它们的结果是一样的,这也验证了测试函数的正确性。
3.具体代码
主函数main1.m代码:
%% 信号处理————频域分析(功率谱和功率谱密度)
clc
clear all
close all
%
fs=1000; %采样频率
L=2000; %信号长度
t=(0:L-1)/fs; %时间序列
y1=0.8+0.7*cos(2*pi*50*t-pi/4)+0.8*cos(2*pi*300*t+pi/5); %信号y1
y11=y1+0.5*randn(size(y1)); %加噪信号y11
y=y11'; %分析的信号,y的列为信号数量维度,y的行为每个信号的索引维度
figure('Position', [100, 100, 600, 100]);
plot(t,y11,'b');xlabel('时间(s)');ylabel('幅值');
[freq,P1,Theta,P1_power,P1_psd]=frequ_am_phase_power_psd(y,fs); %幅值谱和相位谱 相位谱的阈值参数为1e-6
%画图
[P11_power P11_freq_power]=periodogram(y,rectwin(size(y,1)),size(y,1),fs,'power');
[P11_psd P11_freq_psd]=periodogram(y,rectwin(size(y,1)),size(y,1),fs,'psd');
%幅值谱
figure
stem(freq,P1(:,1),'k'); %作图
xlabel('频率(Hz)');ylabel('幅值');title('幅值谱');
%相位谱
figure
stem(freq,Theta(:,1),'k'); %作图
xlabel('频率(Hz)');ylabel('相位 (\pi)');title('相位谱');
%功率谱
figure
plot(freq,pow2db(P1_power(:,1)),'b');hold on; %作图
plot(P11_freq_power,pow2db(P11_power(:,1)),'r');
xlabel('频率(Hz)');ylabel('功率(dB)');title('功率谱');
legend('测试函数','matlab函数');
fprintf('测试信号y的功率谱中测试函数与matlab函数之间的差为%f \n',sum(P1_power(:,1)-P11_power(:,1)));
%功率谱密度
figure
plot(freq,pow2db(P1_psd(:,1)),'b');hold on; %作图
plot(P11_freq_psd,pow2db(P11_psd(:,1)),'r');
xlabel('频率(Hz)');ylabel('功率(dB/HZ)');title('功率谱密度');
legend('测试函数','matlab函数');
fprintf('测试信号y的功率谱密度中测试函数与matlab函数之间的差为%f \n',sum(P1_psd(:,1)-P11_psd(:,1)));幅值谱、相位谱、功率谱和功率谱密度计算函数的相关代码:
function [freq,P1,Theta,P1_power,P1_psd]=frequ_am_phase_power_psd(y,fs,tol)
%% 绘制信号频域的功率谱和功率谱密度
%% 参数解释:
% y: 表示输入信号,它可以为一个矩阵,行X列,具体为单个信号的采样索引X信号数
% 比如y的大小为8192X12,表示一个有12个信号的数据矩阵,每个信号长度为8192
% 注意,如果仅有一个信号,则y应该是一个列向量
% 同时,y的行数尽量为偶数,奇数的话会引起程序索引的警告
% fs:表示采样频率
% tol:相位阈值参数
% freq:表示幅值谱的横轴
% P1:表示幅值谱的纵轴
% Theta:表示相位谱的纵轴
% P1_power:表示功率谱的纵轴
% P1_psd:表示功率谱密度的纵轴
if nargin==2
tol=1e-6; %计算误差的默认阈值
end
L=size(y,1); % 信号长度
% Y=fft(y,2^nextpow2(L)); % FFT 快速傅里叶变换
Y=fft(y,L); % FFT 快速傅里叶变换
freq=(0:L/2)*fs/L; % 设置频率刻度 横轴Hz
%幅值谱
P2 = abs(Y/L);
P1 = P2(1:L/2+1,:);
P1(2:end-1,:) = 2*P1(2:end-1,:); %纵轴 幅值
%相位谱
P2(2:end-1,:)=2*P2(2:end-1,:);
for i=1:size(Y,2)
Y(P2(:,i)<tol,i) = 0;
theta(:,i) = angle(Y(:,i))/pi;
end
Theta=theta(1:L/2+1,:);
%功率谱
P2_power=abs(fft(y,L)).^2/(L^2); %双边功率谱
% P2_power=abs(fft(y,L)).^2/(L); %双边功率谱
P1_power=P2_power(1:L/2+1,:); %单边功率谱
P1_power(2:end-1,:)=2*P1_power(2:end-1,:); %纵轴 功率
%功率谱密度
P2_psd=abs(fft(y,L)).^2/(L*fs); %双边功率谱密度
P1_psd=P2_psd(1:L/2+1,:); %单边功率谱密度
P1_psd(2:end-1,:)=2*P1_psd(2:end-1,:); %纵轴 功率密度
end上述是一个随机信号的功率谱和功率谱密度的示例,采用的是周期图法,在原先封装幅值谱和相位谱的函数基础上增加了功率谱和功率谱密度,方便大家使用,但是关于功率谱和功率谱密度还是推荐matlab的periodogram函数。